Final topology

In general topology and related areas of mathematics, the final topology (or strong topology or colimit topology or projective topology) on a set $X$, with respect to a family of functions into $X$, is the finest topology on X which makes those functions continuous.

The dual notion is the initial topology.

Definition

Given a set $X$ and a family of topological spaces $Y_{i}$ with functions

$f_{i}:Y_{i}\to X$

the final topology $\tau$ on $X$ is the finest topology such that each

$f_{i}:Y_{i}\to (X,\tau )$

is continuous.

Explicitly, the final topology may be described as follows: a subset U of X is open if and only if $f_{i}^{-1}(U)$ is open in Y_i for each i ∈ I.

Examples

• The quotient topology is the final topology on the quotient space with respect to the quotient map.
• The disjoint union is the final topology with respect to the family of canonical injections.
• More generally, a topological space is coherent with a family of subspaces if it has the final topology coinduced by the inclusion maps.
• The direct limit of any direct system of spaces and continuous maps is the set-theoretic direct limit together with the final topology determined by the canonical morphisms.
• Given a family of topologies {τ_i} on a fixed set X the final topology on X with respect to the functions id_X : (X, τ_i) → X is the infimum (or meet) of the topologies {τ_i} in the lattice of topologies on X. That is, the final topology τ is the intersection of the topologies {τ_i}.
• The etale space of a sheaf is topologized by a final topology.

Properties

A subset of $X$ is closed/open if and only if its preimage under f_i is closed/open in $Y_{i}$ for each i ∈ I.

The final topology on X can be characterized by the following universal property: a function $g$ from $X$ to some space $Z$ is continuous if and only if $g\circ f_{i}$ is continuous for each i ∈ I.

Characteristic property of the final topology

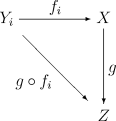
By the universal property of the disjoint union topology we know that given any family of continuous maps f_i : Y_i → X there is a unique continuous map

$f\colon \coprod _{i}Y_{i}\to X$

If the family of maps f_i covers X (i.e. each x in X lies in the image of some f_i) then the map f will be a quotient map if and only if X has the final topology determined by the maps f_i.

Categorical description

In the language of category theory, the final topology construction can be described as follows. Let Y be a functor from a discrete category J to the category of topological spaces Top which selects the spaces Y_i for i in J. Let Δ be the diagonal functor from Top to the functor category Top^J (this functor sends each space X to the constant functor to X). The comma category (Y ↓ Δ) is then the category of cones from Y, i.e. objects in (Y ↓ Δ) are pairs (X, f) where f_i : Y_i → X is a family of continuous maps to X. If U is the forgetful functor from Top to Set and Δ′ is the diagonal functor from Set to Set^J then the comma category (UY ↓ Δ′) is the category of all cones from UY. The final topology construction can then be described as a functor from (UY ↓ Δ′) to (Y ↓ Δ). This functor is left adjoint to the corresponding forgetful functor.

See also

• Initial topology

References

• Stephen Willard, General Topology, (1970) Addison-Wesley Publishing Company, Reading Massachusetts. (Provides a short, general introduction)