Geiger–Müller tube

The Geiger–Müller tube or G–M tube is the sensing element of the Geiger counter instrument used for the detection of ionizing radiation. It was named after Hans Geiger, who invented the principle in 1908,[1] and Walther Müller, who collaborated with Geiger in developing the technique further in 1928 to produce a practical tube that could detect a number of different radiation types.[2][3]
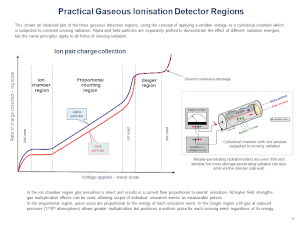
It is a gaseous ionization detector and uses the Townsend avalanche phenomenon to produce an easily detectable electronic pulse from as little as a single ionising event due to a radiation particle. It is used for the detection of gamma radiation, X-rays, and alpha and beta particles. It can also be adapted to detect neutrons. The tube operates in the "Geiger" region of ion pair generation. This is shown on the accompanying plot for gaseous detectors showing ion current against applied voltage.
While it is a robust and inexpensive detector, the G–M is unable to measure high radiation rates efficiently, has a finite life in high radiation areas and cannot measure incident radiation energy, so no spectral information can be generated and there is no discrimination between radiation types; such as between alpha and beta particles.
Principle of operation


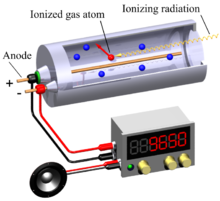
A G-M tube consists of a chamber filled with a gas mixture at a low pressure of about 0.1 atmosphere. The chamber contains two electrodes, between which there is a potential difference of several hundred volts. The walls of the tube are either metal or have their inside surface coated with a conducting material or a spiral wire to form the cathode, while the anode is a wire mounted axially in the centre of the chamber.
When ionizing radiation strikes the tube, some molecules of the fill gas are ionized directly by the incident radiation, and if the tube cathode is an electrical conductor, such as stainless steel, indirectly by means of secondary electrons produced in the walls of the tube, which migrate into the gas. This creates positively charged ions and free electrons, known as ion pairs, in the gas. The strong electric field created by the voltage across the tube's electrodes accelerates the positive ions towards the cathode and the electrons towards the anode. Close to the anode in the "avalanche region" where the electric field strength rises exponentially as the anode is approached, free electrons gain sufficient energy to ionize additional gas molecules by collision and create a large number of electron avalanches. These spread along the anode and effectively throughout the avalanche region. This is the "gas multiplication" effect which gives the tube its key characteristic of being able to produce a significant output pulse from a single original ionising event.[5]
If there were to be only one avalanche per original ionising event, then the number of excited molecules would be in the order of 106 to 108. However the production of multiple avalanches results in an increased multiplication factor which can produce 109 to 1010 ion pairs.[5] The creation of multiple avalanches is due to the production of UV photons in the original avalanche, which are not affected by the electric field and move laterally to the axis of the anode to instigate further ionising events by collision with gas molecules. These collisions produce further avalanches, which in turn produce more photons, and thereby more avalanches in a chain reaction which spreads laterally through the fill gas, and envelops the anode wire. The accompanying diagram shows this graphically. The speed of propagation of the avalanches is typically 2–4 cm per microsecond, so that for common sizes of tubes the complete ionisation of the gas around the anode takes just a few microseconds.[5] This short, intense pulse of current can be measured as a count event in the form of a voltage pulse developed across an external electrical resistor. This can be in the order of volts, thus making further electronic processing simple.
The discharge is terminated by the collective effect of the positive ions created by the avalanches. These ions have lower mobility than the free electrons due to their higher mass and move slowly from the vicinity of the anode wire. This creates a "space charge" which counteracts the electric field that is necessary for continued avalanche generation. For a particular tube geometry and operating voltage this termination always occurs when a certain number of avalanches have been created, therefore the pulses from the tube are always of the same magnitude regardless of the energy of the initiating particle. Consequently, there is no radiation energy information in the pulses[5] which means the Geiger–Muller tube cannot be used to generate spectral information about the incident radiation. In practice the termination of the avalanche is improved by the use of "quenching" techniques (see later).
Pressure of the fill gas is important in the generation of avalanches. Too low a pressure and the efficiency of interaction with incident radiation is reduced. Too high a pressure, and the “mean free path” for collisions between accelerated electrons and the fill gas is too small, and the electrons cannot gather enough energy between each collision to cause ionisation of the gas. The energy gained by electrons is proportional to the ratio “e/p”, where “e” is the electric field strength at that point in the gas, and “p” is the gas pressure.[5]
Types of tube
Broadly, there are two main types of Geiger tube construction.
End window type
For alpha particles, low energy beta particles, and low energy X-rays, the usual form is a cylindrical end-window tube. This type has a window at one end covered in a thin material through which low-penetrating radiation can easily pass. Mica is a commonly used material due to its low mass per unit area. The other end houses the electrical connection to the anode.
Pancake tube

The pancake tube is a variant of the end window tube, but which is designed for use for beta and gamma contamination monitoring. It has roughly the same sensitivity to particles as the end window type, but has a flat annular shape so the largest window area can be utilised with a minimum of gas space. Like the cylindrical end window tube, mica is a commonly used window material due to its low mass per unit area. The anode is normally multi-wired in concentric circles so it extends fully throughout the gas space.
Windowless type
This general type is distinct from the dedicated end window type, but has two main sub-types, which use different radiation interaction mechanisms to obtain a count.
Thick walled

Used for gamma radiation detection above energies of about 25 KeV, this type generally has an overall wall thickness of about 1-2 mm of chrome steel. Because most high energy gamma photons will pass through the low density fill gas without interacting, the tube uses the interaction of photons on the molecules of the wall material to produce high energy secondary electrons within the wall. Some of these electrons are produced close enough to the inner wall of the tube to escape into the fill gas. As soon as this happens the electron drifts to the anode and an electron avalanche occurs as though the free electron had been created within the gas.[5] The avalanche is a secondary effect of a process that starts within the tube wall with the production of electrons that migrate to the inner surface of the tube wall, and then enter the fill gase. This effect is considerably attentuated at low energies below about 20 KeV [4]
Thin walled
Thin walled tubes are used for:
- High energy beta detection, where the beta enters via the side of the tube and interacts directly with the gas, but the radiation has to be energetic enough to penetrate the tube wall. Low energy beta, which would penetrate an end window, would be stopped by the tube wall.
- Low energy gamma and X-ray detection. The lower energy photons interact better with the fill gas so this design concentrates on increasing the volume of the fill gas by using a long thin walled tube and does not use the interaction of photons in the tube wall. The transition from thin walled to thick walled design takes place at the 300–400 keV energy levels. Above these levels thick walled designs are used, and beneath these levels the direct gas ionisation effect is predominant.
Neutron detection
G–M tubes will not detect neutrons since these do not ionise the gas. However, neutron-sensitive tubes can be produced which either have the inside of the tube coated with boron, or the tube contains boron trifluoride or helium-3 as the fill gas. The neutrons interact with the boron nuclei, producing alpha particles, or directly with the helium-3 nuclei producing hydrogen and tritium ions and electrons. These charged particles then trigger the normal avalanche process.
Gas mixtures
The components of the gas fill mixture are an inert gas such as helium, argon or neon which is ionised by incident radiation, and a "quench" gas of 5–10% of an organic vapor or a halogen gas to prevent spurious pulsing by quenching the electron avalanches.[5] This combination of gases is known as a Penning mixture and makes use of the Penning ionization effect.
The modern halogen-filled G–M tube was invented by Sidney H. Liebson in 1947 and has several advantages over the older tubes with organic mixtures.[6] The halogen tube discharge takes advantage of a metastable state of the inert gas atom to more-readily ionize a halogen molecule than an organic vapor, enabling the tube to operate at much lower voltages, typically 400–600 volts instead of 900–1200 volts. While halogen-quenched tubes have greater plateau voltage slopes compared to organic-quenched tubes (an undesirable quality), they have a vastly longer life than tubes quenched with organic compounds. This is because the organic vapor is gradually destroyed by the discharge process (giving organic-quenched tubes a useful life of around 109 events), while the halogen ions can recombine over time (giving halogen-quenched tubes an effectively unlimited lifetime for most uses, although they will still eventually fail at some point due to other ionization-initiated processes that limit the lifetime of all Geiger tubes). For these reasons, the halogen-quenched tube is now the most common.[5]
Geiger plateau

The Geiger plateau is the voltage range in which the G-M tube operates in its correct mode, where ionisation occurs along the length of the anode. If a G–M tube is exposed to a steady radiation source and the applied voltage is increased from zero, it follows the plot of current shown in the "Geiger region" where the gradient flattens; this is the Geiger plateau.[5]
This is shown in more detail in the accompanying Geiger Plateau Curve diagram. If the tube voltage is progressively increased from zero the efficiency of detection will rise until the most energetic radiation starts to produce pulses which can be detected by the electronics. This is the "starting voltage". Increasing the voltage still further results in rapidly rising counts until the "knee" or threshold of the plateau is reached, where the rate of increase of counts falls off. This is where the tube voltage is sufficient to allow a complete discharge along the anode for each detected radiation count, and the effect of different radiation energies are equal. However, the plateau has a slight slope mainly due to the lower electric fields at the ends of the anode because of tube geometry. As the tube voltage is increased, these fields strengthen to produce avalanches. At the end of the plateau the count rate begins to increase rapidly again, until the onset of continuous discharge where the tube cannot detect radiation, and may be damaged.[5].
Depending on the characteristics of the specific tube (manufacturer, size, gas type, etc.) the voltage range of the plateau will vary. The slope is usually expressed as percentage change of counts per 100V. To prevent overall efficiency changes due to variation of tube voltage, a regulated voltage supply is used, and it is normal practice to operate in the middle of the plateau to reduce the effect of any voltage variations. [5][7]
Quenching and dead time

The ideal G–M tube should produce a single pulse for every single ionising event due to radiation. It should not give spurious pulses, and should recover quickly to the passive state, ready for the next radiation event. However, when positive argon ions reach the cathode and become neutral atoms by gaining electrons, the atoms can be elevated to enhanced energy levels. These atoms then return to their ground state by emitting photons which in turn produce further ionisation and thereby spurious secondary discharges. If nothing were done to counteract this, ionisation would be prolonged and could even escalate. The prolonged avalanche would increase the "dead time" when new events cannot be detected, and could become continuous and damage the tube. Some form of quenching of the ionisation is therefore essential to reduce the dead time and protect the tube, and a number of quenching techniques are used.
Chemical quenching
Self-quenching or internal-quenching tubes stop the discharge without external assistance, originally by means of the addition of a small amount of a polyatomic organic vapor originally such as butane or ethanol, but for modern tubes is a halogen such as bromine or chlorine.[5]
If a poor gas quencher is introduced to the tube, the positive argon ions, during their motion toward the cathode, would have multiple collisions with the quencher gas molecules and transfer their charge and some energy to them. Thus, neutral argon atoms would be produced and the quencher gas ions in their turn would reach the cathode, gain electrons therefrom, and move into excited states which would decay by photon emission, producing tube discharge. However, effective quencher molecules, when excited, lose their energy not by photon emission, but by dissociation into neutral quencher molecules. No spurious pulses are thus produced.[5]
Even with chemical quenching, for a short time after a discharge pulse there is a period during which the tube is rendered insensitive and is thus temporarily unable to detect the arrival of any new ionizing particle (the so-called dead time; typically 50–100 microseconds). This causes a loss of counts at sufficiently high count rates and limits the G–M tube to an effective (accurate) count rate of approximately 103 counts per second even with external quenching. While a G-M tube is technically capable of reading higher count rates before it truly saturates, the level of uncertainty involved and the risk of saturation makes it extremely dangerous to rely upon higher count rate readings when attempting to calculate an equivalent radiation dose rate from the count rate. A consequence of this is that ion chamber instruments are usually preferred for higher count rates, however a modern external quenching technique can extend this upper limit considerably.[5]
External quenching
External quenching, sometimes called "active quenching" or "electronic quenching", uses simplistic high speed control electronics to rapidly remove and re-apply the high voltage between the electrodes for a fixed time after each discharge peak in order to increase the maximum count rate and lifetime of the tube. Although this can be used instead of a quench gas, it is much more commonly used in conjunction with a quench gas.[5]
The "time-to-first-count method" is a sophisticated modern implementation of external quenching that allows for dramatically increased maximum count rates via the use of statistical signal processing techniques and much more complex control electronics. Due to uncertainty in the count rate introduced by the simplistic implementation of external quenching, the count rate of a Geiger tube becomes extremely unreliable above approximately 103 counts per second. With the time-to-first-count method, effective count rates of 105 counts per second are achievable, two orders of magnitude larger than the normal effective limit. The time-to-first-count method is significantly more complicated to implement than traditional external quenching methods, and as a result of this it has not seen widespread use.[5]
Fold-back effect
One consequence of the dead time effect is the possibility of a high count rate continually triggering the tube before the recovery time has elapsed. This may produce pulses too small for the counting electronics to detect and lead to the very undesirable situation whereby a G–M counter in a very high radiation field is falsely indicating a low level. This phenomenon is known as "fold-back". An industry rule of thumb is that the discriminator circuit receiving the output from the tube should detect down to 1/10 of the magnitude of a normal pulse to guard against this.[4] Additionally the circuit should detect when "pulse pile-up " has occurred, where the apparent anode voltage has moved to a new dc level through the combination of high pulse count and noise. The electronic design of Geiger–Muller counters must be able to detect this situation and give an alarm; it is normally done by setting a threshold for excessive tube current.
Detection efficiency
The efficiency of detection of a G–M tube varies with the type of incident radiation. Tubes with thin end windows have very high efficiencies (can be nearly 100%) for high energy beta, though this drops off as the beta energy decreases due to attenuation by the window material. Alpha particles are also attenuated by the window. As alpha particles have a maximum range of less than 50 mm in air, the detection window should be as close as possible to the source of radiation. The attenuation of the window adds to the attenuation of air, so the window should have a density as low as 1.5 to 2.0 mg/cm2 to give an acceptable level of detection efficiency. The article on stopping power explains in more detail the ranges for particles types of various energies. The counting efficiency of photon radiation (gamma and X-rays above 25 keV) depends on the efficiency of radiation interaction in the tube wall, which increases with the atomic number of the wall material. Chromium iron is a commonly used material, which gives an efficiency of about 1% over a wide range of energies.[4]
Photon energy compensation
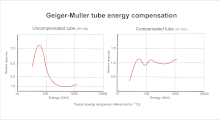


If a G–M tube is to be used for gamma or X-ray dosimetry measurements the energy of incident radiation, which affects the ionising effect, must be taken into account. However pulses from a G–M tube do not carry any energy information, and attribute equal dose to each count event. Consequently the count rate response of a “bare” GM-tube to photons at different energy levels is non-linear with the effect of over-reading at low energies. The variation in dose response can be a factor between 5 to 15, according to individual tube construction; the very small tubes having the highest values.
To correct this a technique known as “Energy Compensation” is applied, which consists of adding a shield of absorbing material round the tube. This filter preferentially absorbs the low energy photons and the dose response is “flattened“. The aim is that sensitivity/energy characteristic of the tube should be matched by the absorption/energy characteristic of the filter. This cannot be exactly achieved, but the result is a more uniform response over the stated range of detection energies for the tube. [5]
Lead and tin are commonly used materials, and a simple filter effective above 150 keV can be made using a continuous collar along the length of the tube. However, at lower energy levels this attenuation can become too great, so air gaps are left in the collar to allow low energy radiation to have a greater effect. In practice, compensation filter design is an empirical compromise to produce an acceptably uniform response, and a number of different materials and geometries are used to obtain the required correction.[4]
See also
- Dosimeter
- Geiger counter
- Gaseous ionization detectors
- Ionization chamber
- Stopping power of radiation particles
References
- ^ Rutherford, E.; Geiger, H. (1908). "An electrical method of counting the number of α particles from radioactive substances". Proceedings of the Royal Society. Series A. 81 (546). London: 141–161. Bibcode:1908RSPSA..81..141R. doi:10.1098/rspa.1908.0065.
- ^ Geiger, H.; Müller, W. (1928). "Elektronenzählrohr zur Messung schwächster Aktivitäten" [Electron counting tube for measurement of weakest radioactivities]. Die Naturwissenschaften (in German). 16 (31): 617–618. Bibcode:1928NW.....16..617G. doi:10.1007/BF01494093.
- ^ See also:
- Geiger, H.; Müller, W. (1928). "Das Elektronenzählrohr" [The electron counting tube]. Physikalische Zeitschrift (in German). 29: 839–841.
- Geiger, H.; Müller, W. (1929). "Technische Bemerkungen zum Elektronenzählrohr" [Technical notes on the electron counting tube]. Physikalische Zeitschrift (in German). 30: 489–493.
- Geiger, H.; Müller, W. (1929). "Demonstration des Elektronenzählrohrs" [Demonstration of the electron counting tube]. Physikalische Zeitschrift (in German). 30: 523 ff.
- ^ a b c d e Centronics Ltd - Geiger Muller tubes, a guide to applications and characteristics
- ^ a b c d e f g h i j k l m n o p q r Glenn F Knoll. Radiation Detection and Measurement, third edition 2000. John Wiley and sons, ISBN 0-471-07338-5
- ^ Liebson, S. H. (1947). "The discharge mechanism of self-quenching Geiger–Mueller counters". Physical Review. 72 (7): 602–608. Bibcode:1947PhRv...72..602L. doi:10.1103/physrev.72.602.
- ^ A Handbook of Radioactivity Measurements Procedures (2nd ed.). National Council on Radiation Protection and Measurements (NCRP). 1985. pp. 30–31. ISBN 0-913392-71-5. Report No. 58.
External links
- Patents
- U.S. patent 1,995,018, H. J. Spanner, "Gas Filled Tube"
- U.S. patent 2,257,827, G. J. Weissenberg, "Electron Discharge Tube"
- U.S. patent 2,521,315, J. A. Victoreen, "Geiger tube"
- U.S. patent 2,542,440, J. A. Victoreen, "Geiger tube"
- Other
