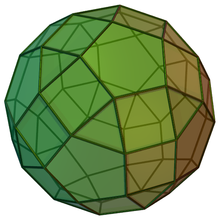
Gyrate rhombicosidodecahedron
| Gyrate rhombicosidodecahedron | |
|---|---|
 | |
| Type | Johnson J71 - J72 - J73 |
| Faces | 4x5 triangles 4x5+10 squares 2+2x5 pentagons |
| Edges | 120 |
| Vertices | 60 |
| Vertex configuration | 10(3.42.5) 4x5+3x10(3.4.5.4) |
| Symmetry group | C5v |
| Dual polyhedron | - |
| Properties | convex |
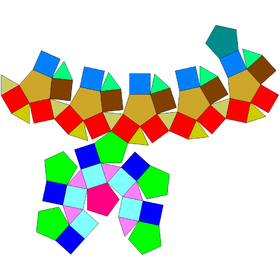
| Net | |
 | |
In geometry, the gyrate rhombicosidodecahedron is one of the Johnson solids (J72).
A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
Related polyhedron
It can be constructed as a rhombicosidodecahedron with one pentagonal cupola rotated through 36 degrees. They have the same faces around each vertex, but vertex configurations along the rotation become a different order, 3.4.4.5.
 Rhombicosidodecahedron |
 Gyrate rhombicosidodecahedron |
Alternative Johnson solids, constructed by rotating different cupolae of a rhombicosidodecahedron, are: the parabigyrate rhombicosidodecahedron (J73) where two opposing cupolae are rotated, the metabigyrate rhombicosidodecahedron (J74) where two non-opposing cupolae are rotated and the trigyrate rhombicosidodecahedron (J75) where three cupolae are rotated.
External links
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |
- ^ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.