Image (category theory)

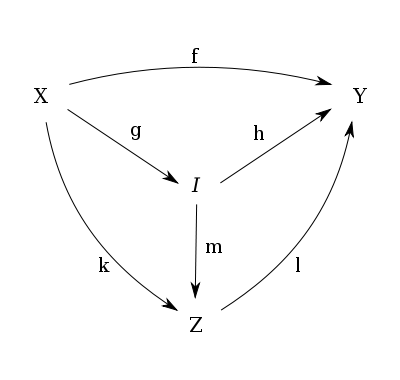
Given a category C and a morphism $f\colon X\to Y$ in C, the image of f is a monomorphism $h\colon I\to Y$ satisfying the following universal property:

1. There exists a morphism $g\colon X\to I$ such that $f=hg$.
2. For any object Z with a morphism $k\colon X\to Z$ and a monomorphism $l\colon Z\to Y$ such that $f=lk$, there exists a unique morphism $m\colon I\to Z$ such that $h=lm$.

Remarks:

1. such a factorization does not necessarily exist
2. g is unique by definition of monic (= left invertible, abstraction of injectivity)
3. m is monic.
4. h=lm already implies that m is unique.
5. k=mg

The image of f is often denoted by im f or Im(f).

One can show that a morphism f is epic if and only if f = im f.

Examples

In the category of sets the image of a morphism $f\colon X\to Y$ is the inclusion from the ordinary image $\{f(x)~|~x\in X\}$ to $Y$. In many concrete categories such as groups, abelian groups and (left- or right) modules, the image of a morphism is the image of the correspondent morphism in the category of sets.

In any normal category with a zero object and kernels and cokernels for every morphism, the image of a morphism $f$ can be expressed as follows:

im f = ker coker f

This holds especially in abelian categories.

See also

• Subobject
• Coimage
• Image (mathematics)

References

• Section I.10 of Mitchell, Barry (1965). Theory of categories. Pure and applied mathematics. Vol. 17. Academic Press. ISBN 978-0-124-99250-4. MR 0202787.