List of small groups

The following list in mathematics contains the finite groups of small order up to group isomorphism.

The list can be used to determine which known group a given finite group G is isomorphic to: first determine the order of G, then look up the candidates for that order in the list below. If you know whether G is abelian or not, some candidates can be eliminated right away. To distinguish between the remaining candidates, look at the orders of your group's elements, and match it with the orders of the candidate group's elements.

Glossary

• Z_n: the cyclic group of order n (often the notation C_n is used, it is isomorphic to Z/nZ).
• Dih_n: the dihedral group of order 2n (often the notation D_n or D_2n is used )
• S_n: the symmetric group of degree n, containing the n! permutations of n elements.
• A_n: the alternating group of degree n, containing the n!/2 even permutations of n elements.
• Dic_n: the dicyclic group of order 4n.

The notations Z_n and Dih_n have the advantage that point groups in three dimensions C_n and D_n do not have the same notation. There are more isometry groups than these two, of the same abstract group type.

The notation G × H stands for the direct product of the two groups; Gⁿ denotes the direct product of a group with itself n times. G $\rtimes$ H stands for a semidirect product where H acts on G; where the particular action of H on G is omitted, it is because all possible non-trivial actions result in the same product group, up to isomorphism.

Abelian and simple groups are noted. (For groups of order n < 60, the simple groups are precisely the cyclic groups Z_n, for prime n.) The equality sign ("=") denotes isomorphism.

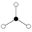
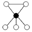
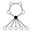
The identity element in the cycle graphs is represented by the black circle. The lowest order for which the cycle graph does not uniquely represent a group is order 16.

In the lists of subgroups the trivial group and the group itself are not listed. Where there are multiple isomorphic subgroups, their number is indicated in parentheses.

List of small abelian groups

The finite abelian groups are easily classified: they are cyclic groups, or direct products thereof; see abelian groups.

Order	Group	Subgroups	Properties	Cycle graph
1	trivial group = Z1 = S1 = A2	-	various properties hold trivially
2	Z2 = S2 = Dih1	-	simple, the smallest non-trivial group
3	Z3 = A3	-	simple
4	Z4	Z2
	Klein four-group = Z2 × Z2 = Dih2	Z2 (3)	the smallest non-cyclic group
5	Z5	-	simple
6	Z6 = Z3 × Z2	Z3 , Z2
7	Z7	-	simple
8	Z8	Z4 , Z2
	Z4 × Z2	Z22, Z4 (2), Z2 (3)
	Z23	Z22 (7) , Z2 (7)	the non-identity elements correspond to the points in the Fano plane, the Z2 × Z2 subgroups to the lines
9	Z9	Z3
	Z32	Z3 (4)
10	Z10 = Z5 × Z2	Z5 , Z2
11	Z11	-	simple
12	Z12 = Z4 × Z3	Z6 , Z4 , Z3 , Z2
	Z6 × Z2 = Z3 × Z22	Z6 (3), Z3, Z2 (3), Z22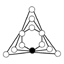
13	Z13	-	simple
14	Z14 = Z7 × Z2	Z7 , Z2
15	Z15 = Z5 × Z3	Z5 , Z3
16	Z16	Z8 , Z4 , Z2
	Z24	Z2 (15) , Z22 (35) , Z23 (15)
	Z4 × Z22	Z2 (7) , Z4 (4) , Z22 (7) , Z23, Z4 × Z2 (6)
	Z8 × Z2	Z2 (3) , Z4 (2) , Z22, Z8 (2) , Z4 × Z2
	Z42	Z2 (3), Z4 (6) , Z22, Z4 × Z2 (3)

List of small non-abelian groups

Order	Group	Subgroups	Properties	Cycle Graph
6	S3 = Dih3	Z3 , Z2 (3)	the smallest non-abelian group
8	Dih4	Z4, Z22 (2) , Z2 (5)
	quaternion group, Q8 = Dic2	Z4 (3), Z2	the smallest Hamiltonian group; smallest group demonstrating that a group need not be abelian, although every subgroup is normal
10	Dih5	Z5 , Z2 (5)
12	Dih6 = Dih3 × Z2	Z6 , Dih3 (2) , Z22 (3) , Z3 , Z2 (7)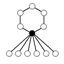
	A4	Z22 , Z3 (4) , Z2 (3)	smallest group demonstrating that a group need not have a subgroup of every order that divides the group's order: no subgroup of order 6 (See Lagrange's theorem and the Sylow theorems.)
	Dic3 = Z3 $\rtimes$ Z4	Z2, Z3, Z4 (3), Z6
14	Dih7	Z7, Z2 (7)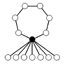
16	Dih8	Z8, Dih4 (2), Z22 (4), Z4, Z2 (9)
	Dih4 × Z2	Dih4 (2), Z4 × Z2, Z23 (2), Z22 (11), Z4 (2), Z2 (11)
	generalized quaternion group, Q16 = Dic4
	Q8 × Z2		Hamiltonian
	The order 16 quasidihedral group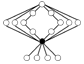
	The order 16 modular group
	Z4 $\rtimes$ Z4
	The group generated by the Pauli matrices
	G4,4 = Z22 $\rtimes$ Z4

Small groups library

The group theoretical computer algebra system GAP contains the "Small Groups library" which provides access to descriptions of small order groups. The groups are listed up to isomorphism. At present, the library contains the following groups:

• those of order at most 2000, except for order 1024 (423164062 groups; the ones of order 1024 had to be skipped, there are alone 49487365422 nonisomorphic 2-groups of order 1024.);
• those of cubefree order at most 50000 (395 703 groups);
• those of squarefree order;
• those of order $p^{n}$ for n at most 6 and p prime;
• those of order $p^{7}$ for p = 3,5,7,11 (907 489 groups);
• those of order qⁿ×p where qⁿ divides 2⁸, 3⁶, 5⁵ or 7⁴ and p is an arbitrary prime which differs from q;
• those whose order factorises into at most 3 primes.

It contains explicit descriptions of the available groups in computer readable format.

See also

• List of finite simple groups
• Small Latin squares and quasigroups

External links

• Small groups
• Besche, Eick and O'Brien's small group library
• Hall, Jr., Marshall; Senior, James K. (1964), The Groups of Order 2n (n ≤ 6), Macmillan, LCCN 64-0 – 0, MR168631. An exhaustive catalog of the 340 groups of order dividing 64 with detailed tables of defining relations, constants, and lattice presentations of each group in the notation the text defines. "Of enduring value to those interested in finite groups" (from the preface).{{citation}}: CS1 maint: postscript (link)