Longitude of periapsis
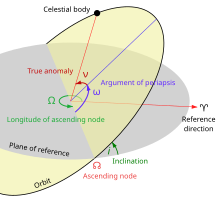
In celestial mechanics, the longitude of the periapsis, also called longitude of the pericenter, of an orbiting body is the longitude (measured from the point of the vernal equinox) at which the periapsis (closest approach to the central body) would occur if the body's orbit inclination were zero. It is usually denoted ϖ.
For the motion of a planet around the Sun, this position is called longitude of perihelion ϖ, which is the sum of the longitude of the ascending node Ω, and the argument of perihelion ω.[1][2]
The longitude of periapsis is a compound angle, with part of it being measured in the plane of reference and the rest being measured in the plane of the orbit. Likewise, any angle derived from the longitude of periapsis (e.g., mean longitude and true longitude) will also be compound.
Sometimes, the term longitude of periapsis is used to refer to ω, the angle between the ascending node and the periapsis. That usage of the term is especially common in discussions of binary stars and exoplanets.[3][4] However, the angle ω is less ambiguously known as the argument of periapsis.
Calculation from state vectors
[edit]ϖ is the sum of the longitude of ascending node Ω (measured on ecliptic plane) and the argument of periapsis ω (measured on orbital plane):
which are derived from the orbital state vectors.
Derivation of ecliptic longitude and latitude of perihelion for inclined orbits
[edit]Define the following:
- i, inclination
- ω, argument of perihelion
- Ω, longitude of ascending node
- ε, obliquity of the ecliptic (for the standard equinox of 2000.0, use 23.43929111°)
Then:
- A = cos ω cos Ω – sin ω sin Ω cos i
- B = cos ε (cos ω sin Ω + sin ω cos Ω cos i) – sin ε sin ω sin i
- C = sin ε (cos ω sin Ω + sin ω cos Ω cos i) + cos ε sin ω sin i
The right ascension α and declination δ of the direction of perihelion are:
If A < 0, add 180° to α to obtain the correct quadrant.
The ecliptic longitude ϖ and latitude b of perihelion are:
If cos(α) < 0, add 180° to ϖ to obtain the correct quadrant.
As an example, using the most up-to-date numbers from Brown (2017)[5] for the hypothetical Planet Nine with i = 30°, ω = 136.92°, and Ω = 94°, then α = 237.38°, δ = +0.41° and ϖ = 235.00°, b = +19.97° (Brown actually provides i, Ω, and ϖ, from which ω was computed).
References
[edit]- ^ Urban, Sean E.; Seidelmann, P. Kenneth (eds.). "Chapter 8: Orbital Ephemerides of the Sun, Moon, and Planets" (PDF). Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 26.
- ^ Simon, J. L.; et al. (1994). "Numerical expressions for precession formulae and mean elements for the Moon and the planets". Astronomy and Astrophysics. 282: 663–683, 672. Bibcode:1994A&A...282..663S.
- ^ Robert Grant Aitken (1918). The Binary Stars. Semicentennial Publications of the University of California. D.C. McMurtrie. p. 201.
- ^ "Format" Archived 2009-02-25 at the Wayback Machine in Sixth Catalog of Orbits of Visual Binary Stars Archived 2009-04-12 at the Wayback Machine, William I. Hartkopf & Brian D. Mason, U.S. Naval Observatory, Washington, D.C. Accessed on 10 January 2018.
- ^ Brown, Michael E. (2017) “Planet Nine: where are you? (part 1)” The Search for Planet Nine. http://www.findplanetnine.com/2017/09/planet-nine-where-are-you-part-1.html
External links
[edit]- Determination of the Earth's Orbital Parameters Past and future longitude of perihelion for Earth.

