Network partition
A network partition refers to network decomposition into relatively independent subnets for their separate optimization as well as network split due to the failure of network devices. In both cases the partition-tolerant behavior of subnets is expected. This means that even after the network is partitioned into multiple sub-systems, it still works correctly.
For example, in a network with multiple subnets where nodes A and B are located in one subnet and nodes C and D are in another, a partition occurs if the switch between the two subnets fails. In that case nodes A and B can no longer communicate with nodes C and D, but all nodes A-D work the same as before.
Network Partition for Optimization
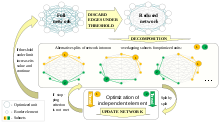
To decompose an NP-hard network optimization task into subtasks, the network can be decomposed into relatively independent subnets. In order to partition the network, it is useful to visualize it as a weighted complete graph, where each vertex corresponds to a network element, and each edge has a weight equal to the rank of the correlation between each pair of corresponding elements. Then the most irrelevant interactions between elements of network are discarded. Based on the remaining connections, the network is then further split into relatively independent subnets.[1] Wherein different allocations of optimized elements predispose alternative splits of the network (Fig. 1). In the case of a large network, the optimization of each subnet can then be performed independently on different computer clusters.
As a CAP trade-off
The CAP Theorem is based on three trade-offs: Consistency, Availability, and Partition tolerance. Partition tolerance, in this context, means the ability of a data processing system to continue processing data even if a network partition causes communication errors between subsystems.[2]
External links
References
- ^ a b Ignatov, D.Yu.; Filippov, A.N.; Ignatov, A.D.; Zhang, X. (2016). "Automatic Analysis, Decomposition and Parallel Optimization of Large Homogeneous Networks" (PDF). Proc. ISP RAS. 28: 141–152. arXiv:1701.06595. doi:10.15514/ISPRAS-2016-28(6)-10.
- ^ Stonebraker, Michael (April 5, 2010). "Errors in Database Systems, Eventual Consistency, and the CAP Theorem". Communications of the ACM.
