Step function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces.
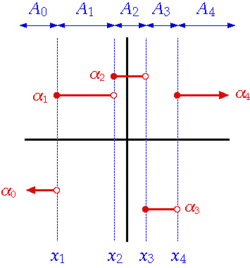
Definition and first consequences
[edit]A function is called a step function if it can be written as [citation needed]
- , for all real numbers
where , are real numbers, are intervals, and is the indicator function of :
In this definition, the intervals can be assumed to have the following two properties:
- The intervals are pairwise disjoint: for
- The union of the intervals is the entire real line:
Indeed, if that is not the case to start with, a different set of intervals can be picked for which these assumptions hold. For example, the step function
can be written as
Variations in the definition
[edit]Sometimes, the intervals are required to be right-open[1] or allowed to be singleton.[2] The condition that the collection of intervals must be finite is often dropped, especially in school mathematics,[3][4][5] though it must still be locally finite, resulting in the definition of piecewise constant functions.
Examples
[edit]
- A constant function is a trivial example of a step function. Then there is only one interval,
- The sign function sgn(x), which is −1 for negative numbers and +1 for positive numbers, and is the simplest non-constant step function.
- The Heaviside function H(x), which is 0 for negative numbers and 1 for positive numbers, is equivalent to the sign function, up to a shift and scale of range (). It is the mathematical concept behind some test signals, such as those used to determine the step response of a dynamical system.
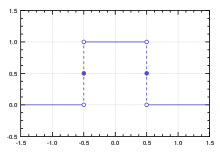
- The rectangular function, the normalized boxcar function, is used to model a unit pulse.
Non-examples
[edit]- The integer part function is not a step function according to the definition of this article, since it has an infinite number of intervals. However, some authors[6] also define step functions with an infinite number of intervals.[6]
Properties
[edit]- The sum and product of two step functions is again a step function. The product of a step function with a number is also a step function. As such, the step functions form an algebra over the real numbers.
- A step function takes only a finite number of values. If the intervals for in the above definition of the step function are disjoint and their union is the real line, then for all
- The definite integral of a step function is a piecewise linear function.
- The Lebesgue integral of a step function is where is the length of the interval , and it is assumed here that all intervals have finite length. In fact, this equality (viewed as a definition) can be the first step in constructing the Lebesgue integral.[7]
- A discrete random variable is sometimes defined as a random variable whose cumulative distribution function is piecewise constant.[8] In this case, it is locally a step function (globally, it may have an infinite number of steps). Usually however, any random variable with only countably many possible values is called a discrete random variable, in this case their cumulative distribution function is not necessarily locally a step function, as infinitely many intervals can accumulate in a finite region.
See also
[edit]- Crenel function
- Piecewise
- Sigmoid function
- Simple function
- Step detection
- Heaviside step function
- Piecewise-constant valuation
References
[edit]- ^ "Step Function".
- ^ "Step Functions - Mathonline".
- ^ "Mathwords: Step Function".
- ^ https://study.com/academy/lesson/step-function-definition-equation-examples.html [bare URL]
- ^ "Step Function".
- ^ a b Bachman, Narici, Beckenstein (5 April 2002). "Example 7.2.2". Fourier and Wavelet Analysis. Springer, New York, 2000. ISBN 0-387-98899-8.
{{cite book}}: CS1 maint: multiple names: authors list (link) - ^ Weir, Alan J (10 May 1973). "3". Lebesgue integration and measure. Cambridge University Press, 1973. ISBN 0-521-09751-7.
- ^ Bertsekas, Dimitri P. (2002). Introduction to Probability. Tsitsiklis, John N., Τσιτσικλής, Γιάννης Ν. Belmont, Mass.: Athena Scientific. ISBN 188652940X. OCLC 51441829.














![{\displaystyle f=0\chi _{(-\infty ,-5)}+4\chi _{[-5,0]}+7\chi _{(0,1)}+3\chi _{[1,6)}+0\chi _{[6,\infty )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5bff43674d124bd16078168fb1aba20c474ca59)








