Poncelet point
Appearance
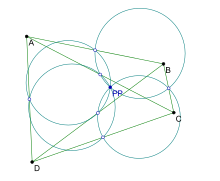
In geometry, the Poncelet point of four given points is defined as follows:
Let A, B, C, and D be four points in the plane that do not form an orthocentric system. The nine-point circles of triangles ABC, BCD, CDA, DAB meet at one point, the Poncelet point of the points A, B, C, and D. If A, B, C, and D be four points in the plane that form an orthocentric system then triangles ABC, BCD, CDA, DAB all share the same nine-point circle.
References
- Vonk, Jan (2009), "The Feuerbach point and reflections of the Euler line" (PDF), Forum Geometricorum, 9: 47–55
