Prismatic compound of antiprisms

Compound of n p/q-gonal antiprisms
n=2 5/3-gonal 5/2-gonal
Type	Uniform compound
Index	q odd: UC23 q even: UC25
Polyhedra	n p/q-gonal antiprisms
Schläfli symbols (n=2)	ß{2,2p/q} ßr{2,p/q}
Coxeter diagrams (n=2)
Faces	2n {p/q} (unless p/q=2), 2np triangles
Edges	4np
Vertices	2np
Symmetry group	nq odd: np-fold antiprismatic (Dnpd) nq even: np-fold prismatic (Dnph)
Subgroup restricting to one constituent	q odd: p-fold antiprismatic (Dpd) q even: p-fold prismatic (Dph)

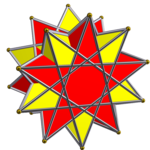
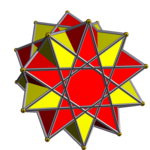
In geometry], a prismatic compound of antiprism is a category of uniform polyhedron compound. Each member of this infinite family of uniform polyhedron compounds is a symmetric arrangement of antiprisms sharing a common axis of rotational symmetry.

Infinite family

This infinite family can be enumerated as follows:

• For each positive integer n≥1 and for each rational number p/q>3/2 (expressed with p and q coprime), there occurs the compound of n p/q-gonal antiprisms, with symmetry group:
  • D_npd if nq is odd
  • D_nph if nq is even

Where p/q=2, the component is the tetrahedron (or dyadic antiprism). In this case, if n=2 then the compound is the stella octangula, with higher symmetry (O_h).

Compounds of two antiprisms

Compounds of two n-antiprisms share their vertices with a 2n-prism, and exist as two alternated set of vertices.

Cartesian coordinates for the vertices of a antiprism with n-gonal bases and isosceles triangles are

• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k}h\right)$
• $\left(\cos {\frac {k\pi }{n}},\sin {\frac {k\pi }{n}},(-1)^{k+1}h\right)$

with k ranging from 0 to 2n−1; if the triangles are equilateral,

$2h^{2}=\cos {\frac {\pi }{n}}-\cos {\frac {2\pi }{n}}.$

Compounds of 2 antiprisms

2 digonal antiprisms (tetrahedra)	2 triangular antiprisms (octahedra)	2 square antiprisms	2 hexagonal antiprisms	2 pentagrammic crossed antiprism

Compound of two trapezohedra (duals)

The duals of the prismatic compound of antiprisms are compounds of trapezohedra:

Two cubes (trigonal trapezohedra)

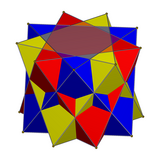
Compound of three antiprisms

For compounds of three digonal antiprisms, they are rotated 60 degrees, while three triangular antiprisms are rotated 40 degrees.

Three tetrahedra	Three octahedra

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.