QM-AM-GM-HM inequalities
This article needs additional citations for verification. (November 2023) |
In mathematics, the QM-AM-GM-HM inequalities, also known as the mean inequality chain, state the relationship between the harmonic mean, geometric mean, arithmetic mean, and quadratic mean (also known as root mean square). Suppose that are positive real numbers. Then
These inequalities often appear in mathematical competitions and have applications in many fields of science.
Proof
[edit]There are three inequalities between means to prove. There are various methods to prove the inequalities, including mathematical induction, the Cauchy–Schwarz inequality, Lagrange multipliers, and Jensen's inequality. For several proofs that GM ≤ AM, see Inequality of arithmetic and geometric means.
AM-QM inequality
[edit]From the Cauchy–Schwarz inequality on real numbers, setting one vector to (1, 1, ...):
- hence . For positive the square root of this gives the inequality.
HM-GM inequality
[edit]The reciprocal of the harmonic mean is the arithmetic mean of the reciprocals , and it exceeds by the AM-GM inequality. implies the inequality:
The n = 2 case
[edit]
When n = 2, the inequalities become
- for all [3]
which can be visualized in a semi-circle whose diameter is [AB] and center D.
Suppose AC = x1 and BC = x2. Construct perpendiculars to [AB] at D and C respectively. Join [CE] and [DF] and further construct a perpendicular [CG] to [DF] at G. Then the length of GF can be calculated to be the harmonic mean, CF to be the geometric mean, DE to be the arithmetic mean, and CE to be the quadratic mean. The inequalities then follow easily by the Pythagorean theorem.
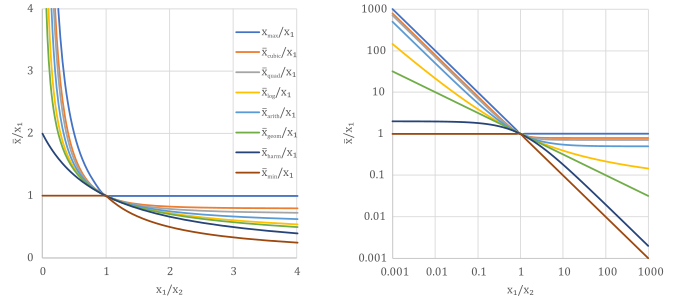
Tests
[edit]To infer the correct order, the four expressions can be evaluated with two positive numbers.
For and in particular, this results in .
See also
[edit]References
[edit]- ^ Djukić, Dušan (2011). The IMO compendium: a collection of problems suggested for the International Mathematical Olympiads, 1959-2009. Problem books in mathematics. International mathematical olympiad. New York: Springer. p. 7. ISBN 978-1-4419-9854-5.
- ^ Sedrakyan, Hayk; Sedrakyan, Nairi (2018), Sedrakyan, Hayk; Sedrakyan, Nairi (eds.), "The HM-GM-AM-QM Inequalities", Algebraic Inequalities, Problem Books in Mathematics, Cham: Springer International Publishing, p. 23, doi:10.1007/978-3-319-77836-5_3, ISBN 978-3-319-77836-5, retrieved 2023-11-26
- ^ Sedrakyan, Hayk; Sedrakyan, Nairi (2018), Sedrakyan, Hayk; Sedrakyan, Nairi (eds.), "The HM-GM-AM-QM Inequalities", Algebraic Inequalities, Problem Books in Mathematics, Cham: Springer International Publishing, p. 21, doi:10.1007/978-3-319-77836-5_3, ISBN 978-3-319-77836-5, retrieved 2023-11-26
External links
[edit]- The HM-GM-AM-QM Inequalities
- Useful inequalities cheat sheet entry "means" on the right of page 1


![{\displaystyle 0<{\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}}\leq {\sqrt[{n}]{x_{1}x_{2}\cdots x_{n}}}\leq {\frac {x_{1}+x_{2}+\cdots +x_{n}}{n}}\leq {\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67057c5febf2a512872008a8a53dc58f9a4bfb03)




![{\displaystyle 1/{\sqrt[{n}]{x_{1}\dots x_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9ae01f87b35eefae3c510c9f64cef1427e24ae2)

![{\displaystyle {\frac {n}{{\frac {1}{x_{1}}}+\dots +{\frac {1}{x_{n}}}}}\leq {\sqrt[{n}]{x_{1}\dots x_{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f4b2233952c31eb61a26630ef67d8e2883b8c9b)






