R-parity
R-parity is a concept in particle physics. In the Minimal Supersymmetric Standard Model, baryon number and lepton number are no longer conserved by all of the renormalizable couplings in the theory. Since baryon number and lepton number conservation have been tested very precisely, these couplings need to be very small in order not to be in conflict with experimental data. R-parity is a symmetry acting on the Minimal Supersymmetric Standard Model (MSSM) fields that forbids these couplings and can be defined as[1]
or, equivalently, as
where s is spin, B is baryon number, and L is lepton number. All Standard Model particles have R-parity of +1 while supersymmetric particles have R-parity of −1.
Note that there are different forms of parity with different effects and principles, one should not confuse this parity with any other parity.
Dark matter candidate
[edit]With R-parity being preserved, the lightest supersymmetric particle (LSP) cannot decay. This lightest particle (if it exists) may therefore account for the observed missing mass of the universe that is generally called dark matter.[2] In order to fit observations, it is assumed that this particle has a mass of 100 GeV/c2 to 1 TeV/c2, is neutral and only interacts through weak interactions and gravitational interactions. It is often called a weakly interacting massive particle or WIMP.
Typically the dark matter candidate of the MSSM is a mixture of the electroweak gauginos and Higgsinos and is called a neutralino. In extensions to the MSSM it is possible to have a sneutrino be the dark matter candidate. Another possibility is the gravitino, which only interacts via gravitational interactions and does not require strict R-parity.
R-parity violating couplings of the MSSM
[edit]The renormalizable R-parity violating couplings of the MSSM are
- violates B by 1 unit
The strongest constraint involving this coupling alone is from the non-observation of neutron–antineutron oscillations.
- violates L by 1 unit
The strongest constraint involving this coupling alone is the violation universality of Fermi constant in quark and leptonic charged current decays.
- violates L by 1 unit
The strongest constraint involving this coupling alone is the violation universality of Fermi constant in leptonic charged current decays.
- violates L by 1 unit
The strongest constraint involving this coupling alone is that it leads to a large neutrino mass.
While the constraints on single couplings are reasonably strong, if multiple couplings are combined together, they lead to proton decay. Thus there are further maximal bounds on values of the couplings from maximal bounds on proton decay rate.
Proton decay
[edit]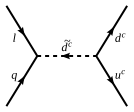
Without baryon and lepton number being conserved and taking couplings for the R-parity violating couplings, the proton can decay in approximately 10−2 seconds or if minimal flavor violation is assumed the proton lifetime can be extended to 1 year. Since the proton lifetime is observed to be greater than 1033 to 1034 years (depending on the exact decay channel), this would highly disfavour the model. R-parity sets all of the renormalizable baryon and lepton number violating couplings to zero and the proton is stable at the renormalizable level and the lifetime of the proton is increased to 1032 years and is nearly consistent with current observational data.
Because proton decay involves violating both lepton and baryon number simultaneously, no single renormalizable R-parity violating coupling leads to proton decay. This has motivated the study of R-parity violation where only one set of the R-parity violating couplings are non-zero which is sometimes called the single coupling dominance hypothesis.
Possible origins of R-parity
[edit]A very attractive way to motivate R-parity is with a B − L continuous gauge symmetry which is spontaneously broken at a scale inaccessible to current experiments. A continuous forbids renormalizable terms which violate B and L.[3][4][5][6] If is only broken by scalar vacuum expectation values (or other order parameters) that carry even integer values of 3(B − L), then there exist an exactly conserved discrete remnant subgroup which has the desired properties.[7][8][9][10][11] The crucial issue is to determine whether the sneutrino (the supersymmetric partner of neutrino), which is odd under R-parity, develops a vacuum expectation value. It can be shown, on phenomenological grounds, that this cannot happen in any theory where is broken at a scale much above the electroweak one. This is true in any theory based on a large-scale seesaw mechanism.[12] As a consequence, in such theories R-parity remains exact at all energies.
This phenomenon can arise as an automatic symmetry in SO(10) grand unified theories. This natural occurrence of R-parity is possible because in SO(10) the Standard Model fermions arise from the 16 dimensional spinor representation, while the Higgs arises from a 10 dimensional vector representation. In order to make an SO(10) invariant coupling, one must have an even number of spinor fields (i.e. there is a spinor parity). After GUT symmetry breaking, this spinor parity descends into R-parity so long as no spinor fields were used to break the GUT symmetry. Explicit examples of such SO(10) theories have been constructed.[13][14]
See also
[edit]References
[edit]- ^ Martin, S. P. (6 Sep 2011). "A Supersymmetry Primer". Advanced Series on Directions in High Energy Physics. 18: 1–98. arXiv:hep-ph/9709356. doi:10.1142/9789812839657_0001. ISBN 978-981-02-3553-6. S2CID 118973381.
- ^ Jungman, G.; Kamionkowski, M.; Griest, K. (1996). "Supersymmetric dark matter". Physics Reports. 267 (5–6): 195–373. arXiv:hep-ph/9506380. Bibcode:1996PhR...267..195J. doi:10.1016/0370-1573(95)00058-5. S2CID 119067698.
- ^ Mohapatra, R.N. (1986). "New contributions to neutrinoless double-beta decay in supersymmetric theories". Physical Review D. 34 (11): 3457–3461. Bibcode:1986PhRvD..34.3457M. doi:10.1103/PhysRevD.34.3457. PMID 9957083.
- ^ Font, A.; Ibáñez, L.E.; Quevedo, F. (1989). "Does proton stability imply the existence of an extra Z0?" (PDF). Physics Letters B. 228 (1): 79–88. Bibcode:1989PhLB..228...79F. doi:10.1016/0370-2693(89)90529-7.
- ^ Martin, S.P. (1992). "Some simple criteria for gauged R parity". Physical Review D. 46 (7): R2769–R2772. arXiv:hep-ph/9207218. Bibcode:1992PhRvD..46.2769M. doi:10.1103/PhysRevD.46.R2769. PMID 10015267. S2CID 14821065.
- ^ Martin, S.P. (1996). "Implications of supersymmetric models with natural R-parity conservation". Physical Review D. 54 (3): 2340–2348. arXiv:hep-ph/9602349. Bibcode:1996PhRvD..54.2340M. doi:10.1103/PhysRevD.54.2340. PMID 10020912. S2CID 5751474.
- ^ Fayet, P. (1975). "Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino". Nuclear Physics B. 90: 104–124. Bibcode:1975NuPhB..90..104F. doi:10.1016/0550-3213(75)90636-7.
- ^ Salam, A.; Strathdee, J. (1975). "Supersymmetry and fermion-number conservation". Nuclear Physics B. 87 (1): 85–92. Bibcode:1975NuPhB..87...85S. doi:10.1016/0550-3213(75)90253-9.
- ^ Farrar, G.R.; Weinberg, S. (1983). "Supersymmetry at ordinary energies. II. R invariance, Goldstone bosons, and gauge-fermion masses". Physical Review D. 27 (11): 2732. Bibcode:1983PhRvD..27.2732F. doi:10.1103/PhysRevD.27.2732.
- ^ Fayet, P. (1977). "Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions". Physics Letters B. 69 (4): 489–494. Bibcode:1977PhLB...69..489F. doi:10.1016/0370-2693(77)90852-8.
- ^ Farrar, G.R.; Fayet, P. (1978). "Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry". Physics Letters B. 76 (5): 575. Bibcode:1978PhLB...76..575F. doi:10.1016/0370-2693(78)90858-4.
- ^ Aulakh, C.S.; Melfo, A.; Rašin, A.; Senjanović, G. (1998). "Supersymmetry and large scale left-right symmetry". Physical Review D. 58 (11): 115007. arXiv:hep-ph/9712551. Bibcode:1998PhRvD..58k5007A. doi:10.1103/PhysRevD.58.115007. S2CID 43296921.
- ^ Aulakh, C.S.; Bajc, B.; Melfo, A.; Rašin, A.; Senjanović, G. (2001). "SO(10) theory of R-parity and neutrino mass". Nuclear Physics B. 597 (1–3): 89–109. arXiv:hep-ph/0004031. Bibcode:2001NuPhB.597...89A. doi:10.1016/S0550-3213(00)00721-5. S2CID 119100803.
- ^ Aulakh, C.S.; Bajc, B.; Melfo, A.; Senjanović, G.; Vissani, F. (2004). "The minimal supersymmetric grand unified theory". Physics Letters B. 588 (3–4): 196–202. arXiv:hep-ph/0306242. Bibcode:2004PhLB..588..196A. doi:10.1016/j.physletb.2004.03.031. S2CID 119401374.
External links
[edit]- Barbier, R.; et al. (2005). "R-parity violating supersymmetry". Physics Reports. 420 (1–6): 1–195. arXiv:hep-ph/0406039. Bibcode:2005PhR...420....1B. doi:10.1016/j.physrep.2005.08.006.
- "R-parity violating ..." xstructure.inr.ac.ru.
- "R-parity violating ..." FNAL. Archived from the original on 2010-05-28.










