Addition principle

In combinatorics, the addition principle[1][2] or rule of sum[3][4] is a basic counting principle. Stated simply, it is the intuitive idea that if we have A number of ways of doing something and B number of ways of doing another thing and we can not do both at the same time, then there are ways to choose one of the actions.[3][1] In mathematical terms, the addition principle states that, for disjoint sets A and B, we have ,[2] provided that the intersection of the sets is without any elements.
The rule of sum is a fact about set theory,[5] as can be seen with the previously mentioned equation for the union of disjoint sets A and B being equal to |A| + |B|.[6]
The addition principle can be extended to several sets. If are pairwise disjoint sets, then we have:[1][2]This statement can be proven from the addition principle by induction on n.[2]
Simple example
[edit]
A person has decided to shop at one store today, either in the north part of town or the south part of town. If they visit the north part of town, they will shop at either a mall, a furniture store, or a jewelry store (3 ways). If they visit the south part of town then they will shop at either a clothing store or a shoe store (2 ways).
Thus there are possible shops the person could end up shopping at today.
Inclusion–exclusion principle
[edit]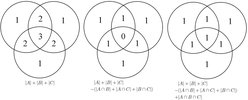
The inclusion–exclusion principle (also known as the sieve principle[7]) can be thought of as a generalization of the rule of sum in that it too enumerates the number of elements in the union of some sets (but does not require the sets to be disjoint). It states that if A1, ..., An are finite sets, then[7]
Subtraction principle
[edit]Similarly, for a given finite set S, and given another set A, if , then .[8][9] To prove this, notice that by the addition principle.[9]
Applications
[edit]This section needs expansion. You can help by adding to it. (November 2022) |
The addition principle can be used to prove Pascal's rule combinatorially. To calculate , one can view it as the number of ways to choose k people from a room containing n children and 1 teacher. Then there are ways to choose people without choosing the teacher, and ways to choose people that includes the teacher. Thus .[10]: 83
The addition principle can also be used to prove the multiplication principle.[2]
References
[edit]- ^ a b c Biggs 2002, p. 91.
- ^ a b c d e mps (22 March 2013). "enumerative combinatorics". PlanetMath. Archived from the original on 23 July 2014. Retrieved 14 August 2021.
- ^ a b Leung, K. T.; Cheung, P. H. (1988-04-01). Fundamental Concepts of Mathematics. Hong Kong University Press. p. 66. ISBN 978-962-209-181-8.
- ^ Penner, R. C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. World Scientific. p. 342. ISBN 978-981-02-4088-2.
- ^ "4.1: Definition and Properties". Mathematics LibreTexts. 2021-08-24. Retrieved 2024-05-02.
- ^ "Rule of sum and rule of product | Combinatorics | Discrete math | Math". Hyperskill. Retrieved 2024-05-02.
- ^ a b Biggs 2002, p. 112.
- ^ Diedrichs, Danilo R. (2022). Transition to advanced mathematics. Stephen Lovett. Boca Raton, FL. p. 172. ISBN 978-1-003-04620-2. OCLC 1302331608.
{{cite book}}: CS1 maint: location missing publisher (link) - ^ a b Moreno, Miguel (2018). "Lecture notes: Combinatorics" (PDF). u.math.biu.ac.il. Archived (PDF) from the original on 19 August 2019. Retrieved 26 November 2022.
- ^ Henry Adams; Kelly Emmrich; Maria Gillespie; Shannon Golden; Rachel Pries (15 November 2021). "Counting Rocks! An Introduction to Combinatorics". arXiv:2108.04902 [math.HO].
Bibliography
[edit]- Biggs, Norman L. (2002). Discrete Mathematics. India: Oxford University Press. ISBN 978-0-19-871369-2.













