Scheinerman's conjecture
In mathematics, Scheinerman's conjecture, now a theorem, states that every planar graph is the intersection graph of a set of line segments in the plane. This conjecture was formulated by E. R. Scheinerman in his Ph.D. thesis (1984), following earlier results that every planar graph could be represented as the intersection graph of a set of simple curves in the plane (Ehrlich, Even & Tarjan 1976). It was proven by Jeremie Chalopin and Daniel Gonçalves (2009).
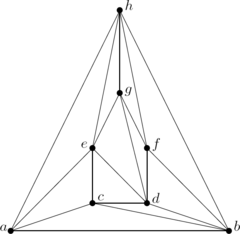
For instance, the graph G shown below to the left may be represented as the intersection graph of the set of segments shown below to the right. Here, vertices of G are represented by straight line segments and edges of G are represented by intersection points.
Scheinerman also conjectured that segments with only three directions would be sufficient to represent 3-colorable graphs, and West (1991) conjectured that analogously every planar graph could be represented using four directions. If a graph is represented with segments having only k directions and no two segments belong to the same line, then the graph can be colored using k colors, one color for each direction. Therefore, if every planar graph can be represented in this way with only four directions, then the four color theorem follows. Gonçalves (2020) proved that some planar graphs cannot be represented in that way.
Hartman, Newman & Ziv (1991) and de Fraysseix, Ossona de Mendez & Pach (1991) proved that every bipartite planar graph can be represented as an intersection graph of horizontal and vertical line segments; for this result see also Czyzowicz, Kranakis & Urrutia (1998). De Castro et al. (2002) proved that every triangle-free planar graph can be represented as an intersection graph of line segments having only three directions; this result implies Grötzsch's theorem (Grötzsch 1959) that triangle-free planar graphs can be colored with three colors. de Fraysseix & Ossona de Mendez (2005) proved that if a planar graph G can be 4-colored in such a way that no separating cycle uses all four colors, then G has a representation as an intersection graph of segments.
Chalopin, Gonçalves & Ochem (2007) proved that planar graphs are in 1-STRING, the class of intersection graphs of simple curves in the plane that intersect each other in at most one crossing point per pair. This class is intermediate between the intersection graphs of segments appearing in Scheinerman's conjecture and the intersection graphs of unrestricted simple curves from the result of Ehrlich et al. It can also be viewed as a generalization of the circle packing theorem, which shows the same result when curves are allowed to intersect in a tangent. The proof of the conjecture by Chalopin & Gonçalves (2009) was based on an improvement of this result.
References
[edit]- De Castro, N.; Cobos, F. J.; Dana, J. C.; Márquez, A. (2002), "Triangle-free planar graphs as segment intersection graphs" (PDF), Journal of Graph Algorithms and Applications, 6 (1): 7–26, doi:10.7155/jgaa.00043, MR 1898201.
- Chalopin, J.; Gonçalves, D. (2009), "Every planar graph is the intersection graph of segments in the plane" (PDF), ACM Symposium on Theory of Computing.
- Chalopin, J.; Gonçalves, D.; Ochem, P. (2007), "Planar graphs are in 1-STRING", Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, ACM and SIAM, pp. 609–617.
- Czyzowicz, J.; Kranakis, E.; Urrutia, J. (1998), "A simple proof of the representation of bipartite planar graphs as the contact graphs of orthogonal straight line segments", Information Processing Letters, 66 (3): 125–126, doi:10.1016/S0020-0190(98)00046-5.
- de Fraysseix, H.; Ossona de Mendez, P. (2005), "Contact and intersection representations", in Pach, J. (ed.), Graph Drawing, 12th International Symposium, GD 2004, Lecture Notes in Computer Science, vol. 3383, Springer-Verlag, pp. 217–227.
- de Fraysseix, H.; Ossona de Mendez, P.; Pach, J. (1991), "Representation of planar graphs by segments", Intuitive Geometry, 63: 109–117, MR 1383616.
- Ehrlich, G.; Even, S.; Tarjan, R. E. (1976), "Intersection graphs of curves in the plane", Journal of Combinatorial Theory, Series B, 21 (1): 8–20, doi:10.1016/0095-8956(76)90022-8, MR 0505857.
- Grötzsch, Herbert (1959), "Zur Theorie der diskreten Gebilde, VII: Ein Dreifarbensatz für dreikreisfreie Netze auf der Kugel", Wiss. Z. Martin-Luther-U., Halle-Wittenberg, Math.-Nat. Reihe, 8: 109–120, MR 0116320.
- Hartman, I. B.-A.; Newman, I.; Ziv, R. (1991), "On grid intersection graphs", Discrete Mathematics, 87 (1): 41–52, doi:10.1016/0012-365X(91)90069-E, MR 1090188.
- Scheinerman, E. R. (1984), Intersection Classes and Multiple Intersection Parameters of Graphs, Ph.D. thesis, Princeton University.
- West, D. (1991), "Open problems #2", SIAM Activity Group Newsletter in Discrete Mathematics, 2 (1): 10–12.
- Gonçalves, Daniel (2020), "Not all planar graphs are in PURE-4-DIR", Journal of Graph Algorithms and Applications, 24 (3): 293–301, doi:10.7155/jgaa.00533.