Section (fiber bundle)

A section s of a bundle p : E → B

A vector field in R². A section of a tangent vector bundle is a vector field.

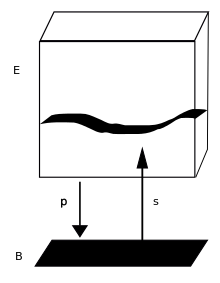
In the mathematical field of topology, a section (or cross section) of a fiber bundle, π: E → B, over a topological space, B, is a continuous map, f : B → E, such that π(f(x))=x for all x in B.

A section is a certain generalization of the notion of the graph of a function. The graph of a function g : X → Y can be identified with a function taking its values in the Cartesian product E = X×Y of X and Y:

$f(x)=(x,g(x))\in E,\quad f:X\to E.$

A section is an abstract characterization of what it means to be a graph. Let π : E → X be the projection onto the first factor: π(x,y) = x. Then a graph is any function f for which π(f(x))=x.

The language of fibre bundles allows this notion of a section to be generalized to the case when E is not necessarily a Cartesian product. If π : E → B is a fibre bundle, then a section is a choice of point f(x) in each of the fibres. The condition π(f(x)) = x simply means that the section at a point x must lie over x. (See image.)

For example, when E is a vector bundle a section of E is an element of the vector space E_x lying over each point x ∈ B. In particular, a vector field on a smooth manifold M is a choice of tangent vector at each point of M: this is a section of the tangent bundle of M. Likewise, a 1-form on M is a section of the cotangent bundle.

Fiber bundles do not in general have such global sections, so it is also useful to define sections only locally. A local section of a fiber bundle is a continuous map f : U → E where U is an open set in B and π(f(x))=x for all x in U. If (U, φ) is a local trivialization of E, where φ is a homeomorphism from π^-1(U) to U × F (where F is the fiber), then local sections always exist over U in bijective correspondence with continuous maps from U to F. The (local) sections form a sheaf over B called the sheaf of sections of E.

The space of continuous sections of a fiber bundle E over U is sometimes denoted C(U,E), while the space of global sections of E is often denoted Γ(E) or Γ(B,E).

Sections are studied in homotopy theory and algebraic topology, where one of the main goals is to account for the existence or non-existence of global sections. This leads to sheaf cohomology and the theory of characteristic classes. For example, a principal bundle has a global section if and only if it is trivial. On the other hand, a vector bundle always has a global section, namely the zero section. However, it only admits a nowhere vanishing section if its Euler class is zero.

Sections, particularly of principal bundles and vector bundles, are also very important tools in differential geometry. In this setting, the base space B is a smooth manifold M, and E is assumed to be a smooth fiber bundle over M (i.e., E is a smooth manifold and π: E → M is a smooth map). In this case, one considers the space of smooth sections of E over an open set U, denoted C^∞(U,E). It is also useful in geometric analysis to consider spaces of sections with intermediate regularity (e.g. C^k sections, or sections with regularity in the sense of Holder conditions or Sobolev spaces).

See also

• Fibration
• Gauge theory
• Principal bundle
• Pullback bundle
• Vector bundle

References

• Norman Steenrod, The Topology of Fibre Bundles, Princeton University Press (1951). ISBN 0-691-00548-6.
• David Bleecker, Gauge Theory and Variational Principles, Addison-Wesley publishing, Reading, Mass (1981). ISBN 0-201-10096-7.

External links

• Fiber Bundle, PlanetMath
• Weisstein, Eric W. "Fiber Bundle". MathWorld.