Tangent–secant theorem
Appearance
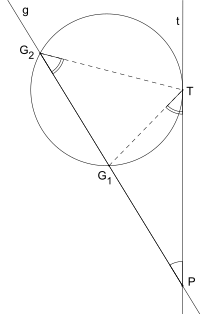
The tangent-secant theorem describes the relation of line segments created by a secant and a tangent line with the associated circle.
For a secant g intersecting the circle in G1 and G2 and tangent t intersecting the circle in T that intersect in P the following equation holds:
The tangent secant theorem can be proven using similar triangles (see graphic). Next to the intersecting chords theorem and the intersecting secants theorem it represents one of the three basic cases of a more general theorem about two intersecting lines and a circle - the power of point theorem.
References
- S. Gottwald: The VNR Concise Encyclopedia of Mathematics. Springer, 2012, ISBN 9789401169820, pp. 175-176
- Michael L. O'Leary: Revolutions in Geometry. Wiley, 2010, ISBN 9780470591796, p. 161
- Schülerduden - Mathematik I. Bibliographisches Institut & F.A. Brockhaus, 8. Auflage, Mannheim 2008, ISBN 978-3-411-04208-1, pp. 415-417 (German)
External links
- Tangent Secant Theorem at proofwiki.org
- Power of a Point Theorem auf cut-the-knot.org
- Weisstein, Eric W. "Chord". MathWorld.




