Tetrahedral prism
| Tetrahedral prism | |
|---|---|
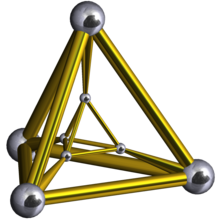 Schlegel diagram | |
| Type | Prismatic uniform 4-polytope |
| Uniform index | 48 |
| Schläfli symbol | t{2,3,3} = {}×{3,3} = h{4,3}×{} s{2,4}×{} sr{2,2}×{} |
| Coxeter diagram | |
| Cells | 2 (3.3.3) 4 (3.4.4) |
| Faces | 8 {3} 6 {4} |
| Edges | 16 |
| Vertices | 8 |
| Vertex configuration | 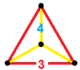 Equilateral-triangular pyramid |
| Dual | Tetrahedral bipyramid |
| Symmetry group | [3,3,2], order 48 [4,2+,2], order 16 [(2,2)+,2], order 8 |
| Properties | convex |
 Net | |
In geometry, a tetrahedral prism is a convex uniform 4-polytope. This 4-polytope has 6 polyhedral cells: 2 tetrahedra connected by 4 triangular prisms. It has 14 faces: 8 triangular and 6 square. It has 16 edges and 8 vertices.
It is one of 18 uniform polyhedral prisms created by using uniform prisms to connect pairs of parallel Platonic solids and Archimedean solids.
Images
[edit]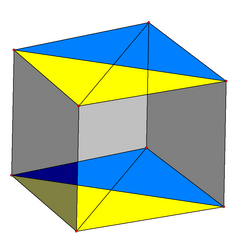 An orthographic projection showing the pair of parallel tetrahedra projected as a quadrilateral divided into yellow and blue triangular faces. Each tetrahedra also have two other uncolored triangles across the opposite diagonal. |
 Transparent Schlegel diagram seen as one tetrahedron nested inside another, with 4 triangular prisms between pairs of triangular faces. |
 Rotating on 2 different planes |
Alternative names
[edit]- Tetrahedral dyadic prism (Norman W. Johnson)
- Tepe (Jonathan Bowers: for tetrahedral prism)
- Tetrahedral hyperprism
- Digonal antiprismatic prism
- Digonal antiprismatic hyperprism
Structure
[edit]The tetrahedral prism is bounded by two tetrahedra and four triangular prisms. The triangular prisms are joined to each other via their square faces, and are joined to the two tetrahedra via their triangular faces.
Projections
[edit]The tetrahedron-first orthographic projection of the tetrahedral prism into 3D space has a tetrahedral projection envelope. Both tetrahedral cells project onto this tetrahedron, while the triangular prisms project to its faces.
The triangular-prism-first orthographic projection of the tetrahedral prism into 3D space has a projection envelope in the shape of a triangular prism. The two tetrahedral cells are projected onto the triangular ends of the prism, each with a vertex that projects to the center of the respective triangular face. An edge connects these two vertices through the center of the projection. The prism may be divided into three non-uniform triangular prisms that meet at this edge; these 3 volumes correspond with the images of three of the four triangular prismic cells. The last triangular prismic cell projects onto the entire projection envelope.
The edge-first orthographic projection of the tetrahedral prism into 3D space is identical to its triangular-prism-first parallel projection.
The square-face-first orthographic projection of the tetrahedral prism into 3D space has a cuboidal envelope (see diagram). Each triangular prismic cell projects onto half of the cuboidal volume, forming two pairs of overlapping images. The tetrahedral cells project onto the top and bottom square faces of the cuboid.
Related polytopes
[edit]It is the first in an infinite series of uniform antiprismatic prisms.
| Name | s{2,2}×{} | s{2,3}×{} | s{2,4}×{} | s{2,5}×{} | s{2,6}×{} | s{2,7}×{} | s{2,8}×{} | s{2,p}×{} |
|---|---|---|---|---|---|---|---|---|
| Coxeter diagram |
||||||||
| Image | 
|

|

|

|

|

|

|

|
| Vertex figure |

|

|
||||||
| Cells | 2 s{2,2} (2) {2}×{}={4} 4 {3}×{} |
2 s{2,3} 2 {3}×{} 6 {3}×{} |
2 s{2,4} 2 {4}×{} 8 {3}×{} |
2 s{2,5} 2 {5}×{} 10 {3}×{} |
2 s{2,6} 2 {6}×{} 12 {3}×{} |
2 s{2,7} 2 {7}×{} 14 {3}×{} |
2 s{2,8} 2 {8}×{} 16 {3}×{} |
2 s{2,p} 2 {p}×{} 2p {3}×{} |
| Net | 
|

|

|
|

|

|

|

|
The tetrahedral prism, -131, is first in a dimensional series of uniform polytopes, expressed by Coxeter as k31 series. The tetrahedral prism is the vertex figure for the second, the rectified 5-simplex. The fifth figure is a Euclidean honeycomb, 331, and the final is a noncompact hyperbolic honeycomb, 431. Each uniform polytope in the sequence is the vertex figure of the next.
| n | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|
| Coxeter group |
A3A1 | A5 | D6 | E7 | = E7+ | =E7++ |
| Coxeter diagram |
||||||
| Symmetry | [3−1,3,1] | [30,3,1] | [31,3,1] | [32,3,1] | [33,3,1] | [34,3,1] |
| Order | 48 | 720 | 23,040 | 2,903,040 | ∞ | |
| Graph | 
|
|

|

|
- | - |
| Name | −131 | 031 | 131 | 231 | 331 | 431 |
References
[edit]- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
External links
[edit]- 6. Convex uniform prismatic polychora - Model 48, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) x x3o3o - tepe".


