Greatest element and least element

In mathematics, especially in order theory, the greatest element of a subset of a partially ordered set (poset) is an element of that is greater than every other element of . The term least element is defined dually, that is, it is an element of that is smaller than every other element of
Definitions
[edit]Let be a preordered set and let An element is said to be a greatest element of if and if it also satisfies:
- for all
By switching the side of the relation that is on in the above definition, the definition of a least element of is obtained. Explicitly, an element is said to be a least element of if and if it also satisfies:
- for all
If is also a partially ordered set then can have at most one greatest element and it can have at most one least element. Whenever a greatest element of exists and is unique then this element is called the greatest element of . The terminology the least element of is defined similarly.
If has a greatest element (resp. a least element) then this element is also called a top (resp. a bottom) of
Relationship to upper/lower bounds
[edit]Greatest elements are closely related to upper bounds.
Let be a preordered set and let An upper bound of in is an element such that and for all Importantly, an upper bound of in is not required to be an element of
If then is a greatest element of if and only if is an upper bound of in and In particular, any greatest element of is also an upper bound of (in ) but an upper bound of in is a greatest element of if and only if it belongs to In the particular case where the definition of " is an upper bound of in " becomes: is an element such that and for all which is completely identical to the definition of a greatest element given before. Thus is a greatest element of if and only if is an upper bound of in .
If is an upper bound of in that is not an upper bound of in (which can happen if and only if ) then can not be a greatest element of (however, it may be possible that some other element is a greatest element of ). In particular, it is possible for to simultaneously not have a greatest element and for there to exist some upper bound of in .
Even if a set has some upper bounds, it need not have a greatest element, as shown by the example of the negative real numbers. This example also demonstrates that the existence of a least upper bound (the number 0 in this case) does not imply the existence of a greatest element either.
Contrast to maximal elements and local/absolute maximums
[edit]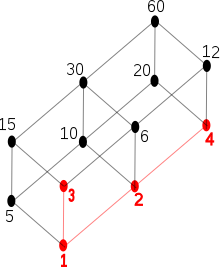
A greatest element of a subset of a preordered set should not be confused with a maximal element of the set, which are elements that are not strictly smaller than any other element in the set.
Let be a preordered set and let An element is said to be a maximal element of if the following condition is satisfied:
- whenever satisfies then necessarily
If is a partially ordered set then is a maximal element of if and only if there does not exist any such that and A maximal element of is defined to mean a maximal element of the subset
A set can have several maximal elements without having a greatest element. Like upper bounds and maximal elements, greatest elements may fail to exist.
In a totally ordered set the maximal element and the greatest element coincide; and it is also called maximum; in the case of function values it is also called the absolute maximum, to avoid confusion with a local maximum.[1] The dual terms are minimum and absolute minimum. Together they are called the absolute extrema. Similar conclusions hold for least elements.
- Role of (in)comparability in distinguishing greatest vs. maximal elements
One of the most important differences between a greatest element and a maximal element of a preordered set has to do with what elements they are comparable to. Two elements are said to be comparable if or ; they are called incomparable if they are not comparable. Because preorders are reflexive (which means that is true for all elements ), every element is always comparable to itself. Consequently, the only pairs of elements that could possibly be incomparable are distinct pairs. In general, however, preordered sets (and even directed partially ordered sets) may have elements that are incomparable.
By definition, an element is a greatest element of if for every ; so by its very definition, a greatest element of must, in particular, be comparable to every element in This is not required of maximal elements. Maximal elements of are not required to be comparable to every element in This is because unlike the definition of "greatest element", the definition of "maximal element" includes an important if statement. The defining condition for to be a maximal element of can be reworded as:
- For all IF (so elements that are incomparable to are ignored) then
- Example where all elements are maximal but none are greatest
Suppose that is a set containing at least two (distinct) elements and define a partial order on by declaring that if and only if If belong to then neither nor holds, which shows that all pairs of distinct (i.e. non-equal) elements in are incomparable. Consequently, can not possibly have a greatest element (because a greatest element of would, in particular, have to be comparable to every element of but has no such element). However, every element is a maximal element of because there is exactly one element in that is both comparable to and that element being itself (which of course, is ).[note 1]
In contrast, if a preordered set does happen to have a greatest element then will necessarily be a maximal element of and moreover, as a consequence of the greatest element being comparable to every element of if is also partially ordered then it is possible to conclude that is the only maximal element of However, the uniqueness conclusion is no longer guaranteed if the preordered set is not also partially ordered. For example, suppose that is a non-empty set and define a preorder on by declaring that always holds for all The directed preordered set is partially ordered if and only if has exactly one element. All pairs of elements from are comparable and every element of is a greatest element (and thus also a maximal element) of So in particular, if has at least two elements then has multiple distinct greatest elements.
Properties
[edit]Throughout, let be a partially ordered set and let
- A set can have at most one greatest element.[note 2] Thus if a set has a greatest element then it is necessarily unique.
- If it exists, then the greatest element of is an upper bound of that is also contained in
- If is the greatest element of then is also a maximal element of [note 3] and moreover, any other maximal element of will necessarily be equal to [note 4]
- Thus if a set has several maximal elements then it cannot have a greatest element.
- If satisfies the ascending chain condition, a subset of has a greatest element if, and only if, it has one maximal element.[note 5]
- When the restriction of to is a total order ( in the topmost picture is an example), then the notions of maximal element and greatest element coincide.[note 6]
- However, this is not a necessary condition for whenever has a greatest element, the notions coincide, too, as stated above.
- If the notions of maximal element and greatest element coincide on every two-element subset of then is a total order on [note 7]
Sufficient conditions
[edit]- A finite chain always has a greatest and a least element.
Top and bottom
[edit]The least and greatest element of the whole partially ordered set play a special role and are also called bottom (⊥) and top (⊤), or zero (0) and unit (1), respectively. If both exist, the poset is called a bounded poset. The notation of 0 and 1 is used preferably when the poset is a complemented lattice, and when no confusion is likely, i.e. when one is not talking about partial orders of numbers that already contain elements 0 and 1 different from bottom and top. The existence of least and greatest elements is a special completeness property of a partial order.
Further introductory information is found in the article on order theory.
Examples
[edit]
- The subset of integers has no upper bound in the set of real numbers.
- Let the relation on be given by The set has upper bounds and but no least upper bound, and no greatest element (cf. picture).
- In the rational numbers, the set of numbers with their square less than 2 has upper bounds but no greatest element and no least upper bound.
- In the set of numbers less than 1 has a least upper bound, viz. 1, but no greatest element.
- In the set of numbers less than or equal to 1 has a greatest element, viz. 1, which is also its least upper bound.
- In with the product order, the set of pairs with has no upper bound.
- In with the lexicographical order, this set has upper bounds, e.g. It has no least upper bound.
See also
[edit]- Essential supremum and essential infimum
- Initial and terminal objects
- Maximal and minimal elements
- Limit superior and limit inferior (infimum limit)
- Upper and lower bounds
- Well-order — a non-strict order such that every non-empty set has a least element
Notes
[edit]- ^ Of course, in this particular example, there exists only one element in that is comparable to which is necessarily itself, so the second condition "and " was redundant.
- ^ If and are both greatest, then and and hence by antisymmetry.
- ^ If is the greatest element of and then By antisymmetry, this renders ( and ) impossible.
- ^ If is a maximal element, then since is greatest, hence since is maximal.
- ^ Only if: see above. — If: Assume for contradiction that has just one maximal element, but no greatest element. Since is not greatest, some must exist that is incomparable to Hence cannot be maximal, that is, must hold for some The latter must be incomparable to too, since contradicts 's maximality while contradicts the incomparability of and Repeating this argument, an infinite ascending chain can be found (such that each is incomparable to and not maximal). This contradicts the ascending chain condition.
- ^ Let be a maximal element, for any either or In the second case, the definition of maximal element requires that so it follows that In other words, is a greatest element.
- ^ If were incomparable, then would have two maximal, but no greatest element, contradicting the coincidence.
References
[edit]- ^ The notion of locality requires the function's domain to be at least a topological space.
- Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). Cambridge University Press. ISBN 978-0-521-78451-1.



































































































