Voltammetry

Voltammetry is a category of electroanalytical methods used in analytical chemistry and various industrial processes. In voltammetry, information about an analyte is obtained by measuring the current as the potential is varied.^[1]^[2] The analytical data for a voltammetric experiment comes in the form of a voltammogram, which plots the current produced by the analyte versus the potential of the working electrode.^[3]

Theory

Voltammetry is the study of current as a function of applied potential. Voltammetric methods involve electrochemical cells, and investigate the reactions occurring at electrode/electrolyte interfaces.^[4] The reactivity of analytes in these half-cells is used to determine their concentration. It is considered a dynamic electrochemical method as the applied potential is varied over time and the corresponding changes in current are measured.^[4] Most experiments control the potential (volts) of an electrode in contact with the analyte while measuring the resulting current (amperes).

Electrochemical cells

Electrochemical cells are used in voltammetric experiments to drive the redox reaction of the analyte. Like other electrochemical cells, two half-cells are required, one to facilitate reduction and the other oxidation. The cell consists of an analyte solution, an ionic electrolyte, and two or three electrodes, with oxidation and reduction reactions occurring at the electrode/electrolyte interfaces.^[5] As a species is oxidized, the electrons produced pass through an external electric circuit and generate a current, acting as an electron source for reduction. The generated currents are Faradaic currents, which follow Faraday's law. As Faraday's law states that the number of moles of a substance, m, produced or consumed during an electrode process is proportional to the electric charge passed through the electrode, the faradaic currents allow analyte concentrations to be determined.^[6] Whether the analyte is reduced or oxidized depends on the analyte, but its reaction always occurs at the working/indicator electrode. Therefore, the working electrode potential varies as a function of the analyte concentration. A second auxiliary electrode completes the electric circuit. A third reference electrode provides a constant, baseline potential reading for the other two electrode potentials to be compared to.

Three electrode system

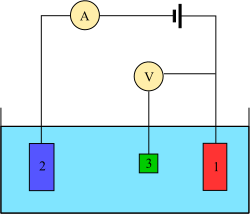
Voltammetry experiments investigate the half-cell reactivity of an analyte. Voltammetry is the study of current as a function of applied potential. These curves I = f(E) are called voltammograms. The potential is varied arbitrarily, either step by step or continuously, and the resulting current value is measured as the dependent variable. The opposite, i.e., amperometry, is also possible but not common. The shape of the curves depends on the speed of potential variation, (nature of driving force) and whether the solution is stirred or quiescent (mass transfer). Most experiments control the potential (volts) of an electrode in contact with the analyte while measuring the resulting current (amperes).^[7]

To conduct such an experiment, at least two electrodes are required. The working electrode, which makes contact with the analyte, must apply the desired potential in a controlled way and facilitate the transfer of charge to and from the analyte. A second electrode acts as the other half of the cell. This second electrode must have a known potential to gauge the potential of the working electrode from; furthermore it must balance the charge added or removed by the working electrode. While this is a viable setup, it has a number of shortcomings. Most significantly, it is extremely difficult for an electrode to maintain a constant potential while passing current to counter redox events at the working electrode.^[7]

To solve this problem, the roles of supplying electrons and providing a reference potential are divided between two separate electrodes. The reference electrode is a half cell with a known reduction potential. Its only role is to act as reference for measuring and controlling the working electrode's potential and it does not pass any current. The auxiliary electrode passes the current required to balance the observed current at the working electrode. To achieve this current, the auxiliary will often swing to extreme potentials at the edges of the solvent window, where it oxidizes or reduces the solvent or supporting electrolyte. These electrodes, the working, reference, and auxiliary make up the modern three-electrode system.^[7]

There are many systems which have more electrodes, but their design principles are similar to the three-electrode system. For example, the rotating ring-disk electrode has two distinct and separate working electrodes, a disk, and a ring, which can be used to scan or hold potentials independently of each other. Both of these electrodes are balanced by a single reference and auxiliary combination for an overall four-electrode design. More complicated experiments may add working electrodes, reference, or auxiliary electrodes as required.^[7]

In practice it can be important to have a working electrode with known dimensions and surface characteristics. As a result, it is common to clean and polish working electrodes regularly. The auxiliary electrode can be almost anything as long as it doesn't react with the bulk of the analyte solution and conducts well. A common voltammetry method, polarography, uses mercury as a working electrode e.g. DME and HMDE, and as an auxiliary electrode. The reference is the most complex of the three electrodes; there are a variety of standards used. For non-aqueous work, IUPAC recommends the use of the ferrocene/ferrocenium couple as an internal standard.^[8] In most voltammetry experiments, a bulk electrolyte (also known as a supporting electrolyte) is used to minimize solution resistance. It is possible to run an experiment without a bulk electrolyte, but the added resistance greatly reduces the accuracy of the results. With room temperature ionic liquids, the solvent can act as the electrolyte.^[7]

Voltammograms

A voltammogram is a graph that measures the current of an electrochemical cell as a function of the potential applied.^[9] This graph is used to determine the concentration and the standard potential of the analyte. To determine the concentration, values such as the limiting or peak current are read from the graph and applied to various mathematical models.^[10] After determining the concentration, the applied standard potential can be identified using the Nernst equation.^[10]

There are three main shapes for voltammograms. The first shape is dependent on the diffusion layer.^[1] If the analyte is continuously stirred, the diffusion layer will be a constant width and produce a voltammogram that reaches a constant current. The graph takes this shape as the current increases from the background residual to reach the limiting current (i_l). If the mixture is not stirred, the width of the diffusion layer eventually increases. This can be observed by the maximum peak current (i_p), and is identified by the highest point on the graph. The third common shape for a voltammogram measures the sample for change in current rather than current applied. A maximum current is still observed, but represents the maximum change in current ( $\Delta$ i_p).^[10]

Mathematical models

To determine analyte concentrations, mathematical models are required to link the applied potential and current measured over time. The Nernst equation relates electrochemical cell potential to the concentration ratio of the reduced and oxidized species in a logarithmic relationship.^[6] The Nernst equation is as follows:

$E=E^{0}-{\frac {RT}{zF}}\ln Q$

Where:

$E$ : Reduction potential
$E^{0}$ : Standard potential
$R$ : Universal gas constant
$T$ : Temperature in kelvin
$z$ : Ion charge (moles of electrons)
$F$ : Faraday constant
$Q$ : Reaction quotient

This equation describes how the changes in applied potential will alter the concentration ratio. However, the Nernst equation is limited, as it is modeled without a time component and voltammetric experiments vary applied potential as a function of time. Other mathematical models, primarily the Butler-Volmer equation, the Tafel equation, and Fick's law address the time dependence.

The Butler–Volmer equation relates concentration, potential, and current as a function of time.^[5] It describes the non-linear relationship between the electrode and electrolyte voltage difference and the electrical current. It helps make predictions about how the forward and backward redox reactions affect potential and influence the reactivity of the cell.^[11] This function includes a rate constant which accounts for the kinetics of the reaction. A compact version of the Butler-Volmer equation is as follows:

${\displaystyle j=j_{0}\cdot \left\{\exp \left[{\frac {\alpha _{\rm {a}}zF\eta }{RT}}\right]-\exp \left[-{\frac {\alpha _{\rm {c}}zF\eta }{RT}}\right]\right\}}$

Where:

$j$ : electrode current density, A/m² (defined as j = I/S)
$j_{0}$ : exchange current density, A/m²
$E$ : electrode potential, V
${\displaystyle E_{\rm {eq}}}$ : equilibrium potential, V
$T$ : absolute temperature, K
$z$ : number of electrons involved in the electrode reaction
$F$ : Faraday constant
$R$ : universal gas constant
$\alpha _{c}$ : so-called cathodic charge transfer coefficient, dimensionless
$\alpha _{a}$ : so-called anodic charge transfer coefficient, dimensionless
$\eta$ : activation overpotential (defined as ${\displaystyle \eta =E-E_{\rm {eq}}}$ ).

At high overpotentials, the Butler–Volmer equation simplifies to the Tafel equation. The Tafel equation relates the electrochemical currents to the overpotential exponentially, and is used to calculate the reaction rate.^[11] The overpotential is calculated at each electrode separately, and related to the voltammogram data to determine reaction rates. The Tafel equation for a single electrode is:

${\displaystyle \eta =\pm A\cdot \log _{10}\left({\frac {i}{i_{0}}}\right)}$

Where:

the plus sign under the exponent refers to an anodic reaction, and a minus sign to a cathodic reaction
$\eta$ : overpotential, V
A: "Tafel slope", V
$i$ : current density, A/m²
$i_{0}$ : "exchange current density", A/m².

As the redox species are oxidized and reduced at the electrodes, material accumulates at the electrode/electrolyte interface.^[5] Material accumulation creates a concentration gradient between the interface and the bulk solution. Fick's laws of diffusion is used to relate the diffusion of oxidized and reduced species to the faradaic current used to describe redox processes. Fick's law is most commonly written in terms of moles, and is as follows:

${\displaystyle J=-D{\frac {d\varphi }{dx}}}$

Where:

J: diffusion flux (in amount of substance per unit area per unit time)
D: diffusion coefficient or diffusivity. (in area per unit time)
φ: concentration (in amount of substance per unit volume)
x: position (in length)

Types of voltammetry

Type of voltammetry	Description
Linear sweep voltammetry	Any voltammetric method where the potential at the working electrode is swept linearly with time, the reference electrode potential remains constant, and measurements are taken of the current at the working electrode.^[12]
Staircase voltammetry	A specialized linear sweep voltammetry technique where voltage is applied for a duration, followed by measurement of current, then repeated for a varying voltages using a staircase program.^[11]
Squarewave voltammetry	Electrochemical method that combines aspects of many pulse voltammetry methods. SWV has a similar waveform to that of DPV but waveform is analyzed as a staircase scan for result interpretation.^[11]
Cyclic voltammetry	A voltammetric method that can be used to determine diffusion coefficients and half cell reduction potentials.^[13]
Anodic stripping voltammetry	A quantitative, analytical method for trace analysis of metal cations. The analyte is deposited (electroplated) onto the working electrode during a deposition step, and then oxidized during the stripping step. The current is measured during the stripping step.^[14]
Cathodic stripping voltammetry	A quantitative, analytical method for trace analysis of anions. A positive potential is applied, oxidizing the mercury electrode and forming insoluble precipitates of the anions. A negative potential then reduces (strips) the deposited film into solution.^[15]
Adsorptive stripping voltammetry	A quantitative, analytical method for trace analysis. The analyte is deposited simply by adsorption on the electrode surface (i.e., no electrolysis), then electrolyzed to give the analytical signal. Chemically modified electrodes are often used.^[16]
Alternating current voltammetry	A type of cyclic voltammetry where small sinusoidal oscillations in voltage are applied to an electrochemical cell while varying the overall voltage.^[17]
Polarography	a subclass of voltammetry where the working electrode is a dropping mercury electrode (DME), useful for its wide cathodic range and renewable surface.^[18]
Rotated electrode voltammetry	A hydrodynamic technique in which the working electrode, usually a rotating disk electrode (RDE) or rotating ring-disk electrode (RRDE), is rotated at a very high rate. This technique is useful for studying the kinetics and electrochemical reaction mechanism for a half reaction.^[19]
Normal pulse polarography	An electrochemical technique where the potential is started at the same value for each step and amplitude is increased for each subsequent step. Measurements of current are taken as function of time and potential between the indicator and reference electrodes.^[20]^[21]
Normal pulse voltammetry	An electrochemical technique that uses the same waveform as normal pulse polarography, but can be used to refer to waveforms of non-polarographic electrodes.^[22]
Differential pulse voltammetry	An electrochemical technique similar to normal pulse voltammetry but the applied base potential is increased or decreased steadily, and the pulse height: base height ratio is kept constant. In DPV, measurements of current are taken twice during each drop, first immediately before the pulse and second before the drop is dislodged.^[11]
Chronoamperometry	An electrochemical experiment type where potential is varied at the working electrode and current is recorded as a function of time.^[11]

History

The beginning of voltammetry was facilitated by the discovery of polarography in 1922 by the Nobel Prize–winning Czech chemist Jaroslav Heyrovský.^[23] Early voltammetric techniques had many problems, limiting their viability for everyday use in analytical chemistry. In polarography, these problems included the fact that mercury is oxidized at a potential that is more positive than +0.2 Volt, making it harder to analyze the results for the analytes in the positive region of the potential. Another problem included the residual current obtained from the charging of the large capacitance of the electrode surface.^[24] When Heyrovsky first recorded the first dependence on the current flowing through the dropping mercury electrode on the applied potential in 1922, he took point-by-point measurements and plotted a current-voltage curve. This was considered to be the first polarogram. In order to facilitate this process, he constructed what is now known as a polarograph with M. Shikata, which enabled him to record photographically the same curve in a matter of hours. He gave recognition to the importance of potential and its control and also recognized the opportunities of measuring the limiting currents. He was also an important part of the introduction of dropping mercury electrode as a modern-day tool.^[25]

In 1942, the English electrochemist Archie Hickling (University of Leicester) built the first three electrodes potentiostat, which was an advancement for the field of electrochemistry.^[26] He used this potentiostat to control the voltage of an electrode. In the meantime, in the late 1940s, the American biophysicist Kenneth Stewart Cole invented an electronic circuit which he called a voltage clamp. The voltage clamp was used to analyze the ionic conduction in nerves.^[27]

The 1960s and 1970s saw many advances in the theory, instrumentation, and the introduction of computer aided and controlled systems. Modern polarographic and voltammetric methods on mercury electrodes came about in three sections.

The first section includes the development of the mercury electrodes. The following electrodes were produced: dropping mercury electrode, mercury steaming electrode, hanging mercury drop electrode, static mercury drop electrode, mercury film electrode, mercury amalgam electrodes, mercury microelectrodes, chemically modified mercury electrodes, controlled growth mercury electrodes, and contractible mercury drop electrodes.

There was also an advancement of the measuring techniques used. These measuring techniques include: classical DC polarography, oscillopolarography, Kaloussek's switcher, AC polarography, tast polarography, normal pulse polarography, differential pulse polarography, square-wave voltammetry, cyclic voltammetry, anodic stripping voltammetry, convolution techniques, and elimination methods.

Lastly, there was also an advancement of preconcentration techniques that produced an increase in the sensitivity of the mercury electrodes. This came about through the development of anodic stripping voltammetry, cathodic stripping voltammetry and adsorptive stripping voltammetry.^[25]

These advancements improved sensitivity and created new analytical methods, which prompted the industry to respond with the production of cheaper potentiostat, electrodes, and cells that could be effectively used in routine analytical work.

Applications

Voltammetric sensors

A number of voltammetric systems are produced commercially for the determination of species that are of interest in industry and research. These devices are sometimes called electrodes but are actually complete voltammetric cells, which are better referred to as sensors. These sensors can be employed for the analysis of organic and inorganic analytes in various matrices.^[28]

The oxygen electrode

The determination of dissolved oxygen in a variety of aqueous environments, such as sea water, blood, sewage, effluents from chemical plants, and soils is of tremendous importance to industry, biomedical and environmental research, and clinical medicine. One of the most common and convenient methods for making such measurements is with the Clark oxygen sensor, which was patented by L.C. Clark, Jr. in 1956.

References

^ ^a ^b Peter T. Kissinger; William R. Heineman, eds. (1996). Laboratory techniques in electroanalytical chemistry (2nd ed.). New York: Marcel Dekker. ISBN 0-8247-9445-1. OCLC 33359917.
^ Zoski, Cynthia G. (2007-02-07). Handbook of Electrochemistry. Elsevier Science. ISBN 978-0-444-51958-0.
^ Harris, Daniel C. (2016-01-01). Quantitative Chemical Analysis, Ninth Edition (9 ed.). W.H. Freeman and Company. ISBN 978-1-4641-3538-5.
^ ^a ^b ^c ^d ^e Harvey, David (2000). Modern analytical chemistry. Boston: McGraw-Hill. ISBN 0-07-237547-7. OCLC 41070677.
^ ^a ^b ^c Kounaves, S.P., 1997. Voltammetric techniques. Handbook of instrumental techniques for analytical chemistry, pp.709-726.
^ ^a ^b Scholz, Fritz (December 2015). "Voltammetric techniques of analysis: the essentials". ChemTexts. 1 (4): 17. doi:10.1007/s40828-015-0016-y. ISSN 2199-3793. S2CID 98262000.
^ ^a ^b ^c ^d ^e Bard, Allen J.; Larry R. Faulkner (2000-12-18). Electrochemical Methods: Fundamentals and Applications (2 ed.). Wiley. ISBN 0-471-04372-9.
^ Gritzner, G.; J. Kuta (1984). "Recommendations on reporting electrode potentials in nonaqueous solvents". Pure Appl. Chem. 56 (4): 461–466. doi:10.1351/pac198456040461. Retrieved 2009-04-17.
^ "voltammogram". Voltammogram | instrument | Britannica. Encyclopedia Britannica. Retrieved 2022-10-24.
^ ^a ^b ^c Harvey, David (2000). Modern analytical chemistry. Boston: McGraw-Hill. ISBN 0-07-237547-7. OCLC 41070677.
^ ^a ^b ^c ^d ^e ^f Bard, Allen J. (2001). Electrochemical methods: fundamentals and applications. Larry R. Faulkner (2nd ed.). Hoboken, NJ. ISBN 0-471-04372-9. OCLC 43859504.{{cite book}}: CS1 maint: location missing publisher (link)
^ Skoog, Douglas A. (2018). Principles of instrumental analysis. F. James Holler, Stanley R. Crouch (7th ed.). Australia. ISBN 978-1-305-57721-3. OCLC 986919158.{{cite book}}: CS1 maint: location missing publisher (link)
^ "11.4: Voltammetric Methods". Chemistry LibreTexts. 2016-12-24. Retrieved 2022-11-09.
^ Thomas, F. G. (2001). Introduction to voltammetric analysis: theory and practice. Günter Henze. Collingwood, Vic.: CSIRO Pub. ISBN 978-0-643-06593-2. OCLC 711261475.
^ Achterberg, E.P.; Barriada, J.L.; Braungardt, C.B. (2005), "VOLTAMMETRY | Cathodic Stripping", Encyclopedia of Analytical Science, Elsevier, pp. 203–211, doi:10.1016/b0-12-369397-7/00649-x, ISBN 978-0-12-369397-6, retrieved 2022-11-09
^ Wang, Joseph (1985). Stripping analysis: principles, instrumentation, and applications. VCH. ISBN 0-89573-143-6. OCLC 299394898.
^ "AC Cyclic Voltammetry". Department of Chemical Engineering and Biotechnology. 2013-11-14. Retrieved 2022-10-22.
^ Reinmuth, W. H. (1961-11-01). "Theory of Stationary Electrode Polarography". Analytical Chemistry. 33 (12): 1793–1794. doi:10.1021/ac60180a004. ISSN 0003-2700.
^ Holze, Rudolf (2002-02-15). "Book Review: Electrochemical Methods. Fundamentals and Applications (2nd Edition). By Allen J. Bard and Larry R. Faulkner". Angewandte Chemie International Edition. 41 (4): 655–657. doi:10.1002/1521-3773(20020215)41:4<655::aid-anie655>3.0.co;2-i. ISSN 1433-7851.
^ "Ontology". www.rsc.org. Retrieved 2022-10-23.
^ "Definition of normal_pulse_polarography_npp - Chemistry Dictionary". www.chemicool.com. Retrieved 2022-10-23.
^ "Normal Pulse Voltammetry (NPV)". Pine Research Instrumentation Store. 2019-03-06. Retrieved 2022-10-23.
^ Budnikov, G. K.; Shirokova, V. I. (2009-12-05). "History of voltammetry in Russia". Journal of Analytical Chemistry. 64 (12): 1279. doi:10.1134/S1061934809120144. ISSN 1608-3199. S2CID 93836045.
^ Kounaves, Samuel. "Voltammetric Techniques". Tufts University Department of Chemistry
^ ^a ^b Barek, J. (2003). "Eighty Years of Polarography - History and Future". Electroanalysis. 15 (5–6): 467–472. doi:10.1002/elan.200390055.
^ Hickling, A. (1942). "Studies in electrode polarisation. Part IV.-The automatic control of the potential of a working electrode". Transactions of the Faraday Society. 38: 27–33. doi:10.1039/TF9423800027.
^ Jackson E. Harrar (2013). "The potentiostat and the voltage clamp" (PDF). electrochem.org. Retrieved 2021-12-15.
^ Sanghavi, Bankim; Srivastava, Ashwini (2010). "Simultaneous voltammetric determination of acetaminophen, aspirin and caffeine using an in situ surfactant-modified multiwalled carbon nanotube paste electrode". Electrochimica Acta. 55 (28): 8638–8648. doi:10.1016/j.electacta.2010.07.093.

External links

[Kissinger_Heineman_1996-1] Peter T. Kissinger; William R. Heineman, eds. (1996). Laboratory techniques in electroanalytical chemistry (2nd ed.). New York: Marcel Dekker. ISBN 0-8247-9445-1. OCLC 33359917.

[2] Zoski, Cynthia G. (2007-02-07). Handbook of Electrochemistry. Elsevier Science. ISBN 978-0-444-51958-0.

[3] Harris, Daniel C. (2016-01-01). Quantitative Chemical Analysis, Ninth Edition (9 ed.). W.H. Freeman and Company. ISBN 978-1-4641-3538-5.

[:1-4] Harvey, David (2000). Modern analytical chemistry. Boston: McGraw-Hill. ISBN 0-07-237547-7. OCLC 41070677.

[:112-5] Kounaves, S.P., 1997. Voltammetric techniques. Handbook of instrumental techniques for analytical chemistry, pp.709-726.

[:102-6] Scholz, Fritz (December 2015). "Voltammetric techniques of analysis: the essentials". ChemTexts. 1 (4): 17. doi:10.1007/s40828-015-0016-y. ISSN 2199-3793. S2CID 98262000.

[:0-7] Bard, Allen J.; Larry R. Faulkner (2000-12-18). Electrochemical Methods: Fundamentals and Applications (2 ed.). Wiley. ISBN 0-471-04372-9.

[8] Gritzner, G.; J. Kuta (1984). "Recommendations on reporting electrode potentials in nonaqueous solvents". Pure Appl. Chem. 56 (4): 461–466. doi:10.1351/pac198456040461. Retrieved 2009-04-17.

[9] "voltammogram". Voltammogram | instrument | Britannica. Encyclopedia Britannica. Retrieved 2022-10-24.

[:12-10] Harvey, David (2000). Modern analytical chemistry. Boston: McGraw-Hill. ISBN 0-07-237547-7. OCLC 41070677.

[:05-11] ^ ^a ^b ^c ^d ^e ^f Bard, Allen J. (2001). Electrochemical methods: fundamentals and applications. Larry R. Faulkner (2nd ed.). Hoboken, NJ. ISBN 0-471-04372-9. OCLC 43859504.{{cite book}}: CS1 maint: location missing publisher (link)

[:2-12] Skoog, Douglas A. (2018). Principles of instrumental analysis. F. James Holler, Stanley R. Crouch (7th ed.). Australia. ISBN 978-1-305-57721-3. OCLC 986919158.{{cite book}}: CS1 maint: location missing publisher (link)

[:7-13] "11.4: Voltammetric Methods". Chemistry LibreTexts. 2016-12-24. Retrieved 2022-11-09.

[:8-14] Thomas, F. G. (2001). Introduction to voltammetric analysis: theory and practice. Günter Henze. Collingwood, Vic.: CSIRO Pub. ISBN 978-0-643-06593-2. OCLC 711261475.

[:9-15] Achterberg, E.P.; Barriada, J.L.; Braungardt, C.B. (2005), "VOLTAMMETRY | Cathodic Stripping", Encyclopedia of Analytical Science, Elsevier, pp. 203–211, doi:10.1016/b0-12-369397-7/00649-x, ISBN 978-0-12-369397-6, retrieved 2022-11-09

[16] Wang, Joseph (1985). Stripping analysis: principles, instrumentation, and applications. VCH. ISBN 0-89573-143-6. OCLC 299394898.

[:3-17] "AC Cyclic Voltammetry". Department of Chemical Engineering and Biotechnology. 2013-11-14. Retrieved 2022-10-22.

[18] Reinmuth, W. H. (1961-11-01). "Theory of Stationary Electrode Polarography". Analytical Chemistry. 33 (12): 1793–1794. doi:10.1021/ac60180a004. ISSN 0003-2700.

[19] Holze, Rudolf (2002-02-15). "Book Review: Electrochemical Methods. Fundamentals and Applications (2nd Edition). By Allen J. Bard and Larry R. Faulkner". Angewandte Chemie International Edition. 41 (4): 655–657. doi:10.1002/1521-3773(20020215)41:4<655::aid-anie655>3.0.co;2-i. ISSN 1433-7851.

[:4-20] "Ontology". www.rsc.org. Retrieved 2022-10-23.

[:5-21] "Definition of normal_pulse_polarography_npp - Chemistry Dictionary". www.chemicool.com. Retrieved 2022-10-23.

[:6-22] "Normal Pulse Voltammetry (NPV)". Pine Research Instrumentation Store. 2019-03-06. Retrieved 2022-10-23.

[23] Budnikov, G. K.; Shirokova, V. I. (2009-12-05). "History of voltammetry in Russia". Journal of Analytical Chemistry. 64 (12): 1279. doi:10.1134/S1061934809120144. ISSN 1608-3199. S2CID 93836045.

[24] Kounaves, Samuel. "Voltammetric Techniques". Tufts University Department of Chemistry

[electroanalysis467-25] Barek, J. (2003). "Eighty Years of Polarography - History and Future". Electroanalysis. 15 (5–6): 467–472. doi:10.1002/elan.200390055.

[26] Hickling, A. (1942). "Studies in electrode polarisation. Part IV.-The automatic control of the potential of a working electrode". Transactions of the Faraday Society. 38: 27–33. doi:10.1039/TF9423800027.

[Harrar-27] Jackson E. Harrar (2013). "The potentiostat and the voltage clamp" (PDF). electrochem.org. Retrieved 2021-12-15.

[28] Sanghavi, Bankim; Srivastava, Ashwini (2010). "Simultaneous voltammetric determination of acetaminophen, aspirin and caffeine using an in situ surfactant-modified multiwalled carbon nanotube paste electrode". Electrochimica Acta. 55 (28): 8638–8648. doi:10.1016/j.electacta.2010.07.093.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

v t e Electroanalytical methods
Techniques	Adsorptive stripping voltammetry Amperometric titration Anodic stripping voltammetry Bulk electrolysis Cathodic stripping voltammetry Chronoamperometry Coulometry Cyclic voltammetry Differential pulse voltammetry Electrogravimetry Hydrodynamic technique Linear sweep voltammetry Normal pulse voltammetry Polarography Potentiometry Rotated electrode voltammetry Squarewave voltammetry Staircase voltammetry Voltammetry
Instrumentation	Amperostat Auxiliary electrode Dropping mercury electrode Electrode Electrolytic cell Galvanic cell Hanging mercury drop electrode Ion selective electrode Mercury coulometer pH meter Potentiostat Reference electrode Rotating disk electrode Rotating ring-disk electrode Salt bridge Saturated calomel electrode Silver chloride electrode Standard hydrogen electrode Ultramicroelectrode Voltameter Working electrode
Theory	Activity coefficient Butler–Volmer equation Cell notation Cottrell equation Debye–Hückel equation Double layer Faraday's laws of electrolysis Half-reaction Ionic strength Nernst equation
Analytical Chemistry

Voltammetry

Theory

Electrochemical cells

Three electrode system

Voltammograms

Mathematical models

Types of voltammetry

History

Applications

Voltammetric sensors

The oxygen electrode

See also

References

Further reading

External links