Weighting
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages)
|




The process of weighting involves emphasizing the contribution of particular aspects of a phenomenon (or of a set of data) over others to an outcome or result; thereby highlighting those aspects in comparison to others in the analysis. That is, rather than each variable in the data set contributing equally to the final result, some of the data is adjusted to make a greater contribution than others. This is analogous to the practice of adding (extra) weight to one side of a pair of scales in order to favour either the buyer or seller.
While weighting may be applied to a set of data, such as epidemiological data, it is more commonly applied to measurements of light, heat, sound, gamma radiation, and in fact any stimulus that is spread over a spectrum of frequencies.
Weighting and loudness[edit]
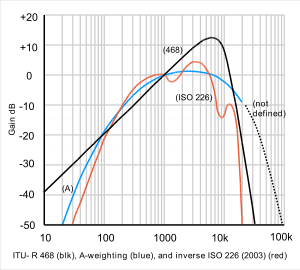
In the measurement of loudness, for example, a weighting filter is commonly used to emphasise frequencies around 3 to 6 kHz where the human ear is most sensitive, while attenuating very high and very low frequencies to which the ear is insensitive. A commonly used weighting is the A-weighting curve, which results in units of dBA sound pressure level. Because the frequency response of human hearing varies with loudness, the A-weighting curve is correct only at a level of 40-phon and other curves known as B-, C- and D-weighting are also used, the latter being particularly intended for the measurement of aircraft noise.
Weighting in audio measurement[edit]
In broadcasting and audio equipment measurements 468-weighting is the preferred weighting to use because it was specifically devised to allow subjectively valid measurements on noise, rather than pure tones. It is often not realised that equal loudness curves, and hence A-weighting, really apply only to tones, as tests with noise bands show increased sensitivity in the 5 to 7 kHz region on noise compared to tones.
Other weighting curves are used in rumble measurement and flutter measurement to properly assess subjective effect.
In each field of measurement, special units are used to indicate a weighted measurement as opposed to a basic physical measurement of energy level. For sound, the unit is the phon (1 kHz equivalent level).
In the fields of acoustics and audio engineering, it is common to use a standard curve referred to as A-weighting, one of a set that are said to be derived from equal-loudness contours.
Weighting and gamma rays[edit]
In the measurement of gamma rays or other ionising radiation, a radiation monitor or dosimeter will commonly use a filter to attenuate those energy levels or wavelengths that cause the least damage to the human body but letting through those that do the most damage, so any source of radiation may be measured in terms of its true danger rather than just its strength. The resulting unit is the sievert or microsievert.
Weighting and television colour components[edit]
Another use of weighting is in television, in which the red, green and blue components of the signal are weighted according to their perceived brightness. This ensures compatibility with black and white receivers and also benefits noise performance and allows separation into meaningful luminance and chrominance signals for transmission.
Weighting and UV factor derivation for sun exposure[edit]
Skin damage due to sun exposure is very wavelength dependent over the UV range 295 to 325 nm, with power at the shorter wavelength causing around 30 times as much damage as the longer one. In the calculation of UV Index, a weighting curve is used which is known as the McKinlay-Diffey Erythema action spectrum.[1] Archived 2010-06-13 at the Wayback Machine
See also[edit]
- Audio quality measurement
- G-weighting
- M-weighting
- Z-weighting
- ITU-R 468 noise weighting
- Psophometric weighting
- Weight function
External links[edit]
- Noise measurement briefing Archived 2008-06-30 at the Wayback Machine
- Calculator for A,C,U, and AU weighting values
- A-weighting filter circuit for audio measurements Archived 2016-12-31 at the Wayback Machine
- AES pro audio reference definition of "weighting filters"
- What is a decibel?
- Weighting filter according DIN EN 61672-1 2003-10 (DIN-IEC 651) Calculation: frequency f to dBA and dBC
