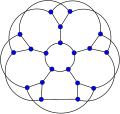
Flower snark
| Flower snark | |
|---|---|
 The flower snarks J3, J5 and J7. | |
| Vertices | 4n |
| Edges | 6n |
| Girth | 3 for n=3 5 for n=5 6 for n≥7 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Book thickness | 3 for n=5 3 for n=7 |
| Queue number | 2 for n=5 2 for n=7 |
| Properties | Snark for n≥5 |
| Notation | Jn with n odd |
| Table of graphs and parameters | |
| Flower snark J5 | |
|---|---|
 The flower snark J5. | |
| Vertices | 20 |
| Edges | 30 |
| Girth | 5 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Properties | Snark Hypohamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.[1]
As snarks, the flower snarks are connected, bridgeless cubic graphs with chromatic index equal to 4. The flower snarks are non-planar and non-Hamiltonian. The flower snarks J5 and J7 have book thickness 3 and queue number 2.[2]
Construction
[edit]The flower snark Jn can be constructed with the following process :
- Build n copies of the star graph on 4 vertices. Denote the central vertex of each star Ai and the outer vertices Bi, Ci and Di. This results in a disconnected graph on 4n vertices with 3n edges (Ai – Bi, Ai – Ci and Ai – Di for 1 ≤ i ≤ n).
- Construct the n-cycle (B1... Bn). This adds n edges.
- Finally construct the 2n-cycle (C1... CnD1... Dn). This adds 2n edges.
By construction, the Flower snark Jn is a cubic graph with 4n vertices and 6n edges. For it to have the required properties, n should be odd.
Special cases
[edit]The name flower snark is sometimes used for J5, a flower snark with 20 vertices and 30 edges.[3] It is one of 6 snarks on 20 vertices (sequence A130315 in the OEIS). The flower snark J5 is hypohamiltonian.[4]
J3 is a trivial variation of the Petersen graph formed by replacing one of its vertices by a triangle. This graph is also known as the Tietze's graph.[5] In order to avoid trivial cases, snarks are generally restricted to have girth at least 5. With that restriction, J3 is not a snark.
Gallery
[edit]-
The chromatic number of the flower snark J5 is 3.
-
The chromatic index of the flower snark J5 is 4.
-
The original representation of the flower snark J5.
-
The Petersen graph as a graph minor of the flower snark J5
References
[edit]- ^ Isaacs, R. (1975). "Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable". Amer. Math. Monthly. 82: 221–239. doi:10.1080/00029890.1975.11993805. JSTOR 2319844.
- ^ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ^ Weisstein, Eric W. "Flower Snark". MathWorld.
- ^ Weisstein, Eric W. "Hypohamiltonian Graph". MathWorld.
- ^ Clark, L.; Entringer, R. (1983), "Smallest maximally nonhamiltonian graphs", Periodica Mathematica Hungarica, 14 (1): 57–68, doi:10.1007/BF02023582.