Multiplicative cascade
In mathematics, a multiplicative cascade[1][2] is a fractal/multifractal distribution of points produced via an iterative and multiplicative random process.
Definition
[edit]The plots above are examples of multiplicative cascade multifractals.
To create these distributions there are a few steps to take. Firstly, we must create a lattice of cells which will be our underlying probability density field.
Secondly, an iterative process is followed to create multiple levels of the lattice: at each iteration the cells are split into four equal parts (cells). Each new cell is then assigned a probability randomly from the set without replacement, where . This process is continued to the Nth level. For example, in constructing such a model down to level 8 we produce a 48 array of cells.
Thirdly, the cells are filled as follows: We take the probability of a cell being occupied as the product of the cell's own pi and those of all its parents (up to level 1). A Monte Carlo rejection scheme is used repeatedly until the desired cell population is obtained, as follows: x and y cell coordinates are chosen randomly, and a random number between 0 and 1 is assigned; the (x, y) cell is then populated depending on whether the assigned number is lesser than (outcome: not populated) or greater or equal to (outcome: populated) the cell's occupation probability.
Examples
[edit]
Generators (left to right): , ,
To produce the plots above we filled the probability density field with 5,000 points in a space of 256 × 256.
An example of the probability density field:
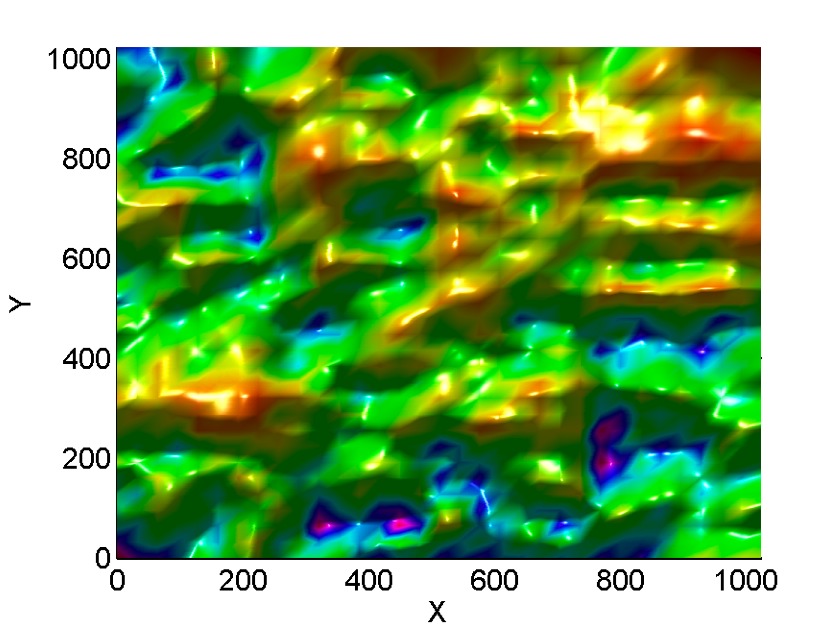
The fractals are generally not scale-invariant and therefore cannot be considered standard fractals. They can however be considered multifractals. The Rényi (generalized) dimensions can be theoretically predicted. It can be shown [3] that as ,
where N is the level of the grid refinement and,
See also
[edit]References
[edit]- ^ Meakin, Paul (September 1987). "Diffusion-limited aggregation on multifractal lattices: A model for fluid-fluid displacement in porous media". Physical Review A. 36 (6): 2833–2837. doi:10.1103/PhysRevA.36.2833. PMID 9899187.
- ^ Cristano G. Sabiu, Luis Teodoro, Martin Hendry, arXiv:0803.3212v1 Resolving the universe with multifractals
- ^ Martinez et al. ApJ 357 50M "Clustering Paradigms and Multifractal Measures" [1]


![{\displaystyle p_{i}\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14760da7a7625a3070329a16c4c37033424871fe)





