Pentagrammic antiprism
| Uniform pentagrammic antiprism | |
|---|---|
| |
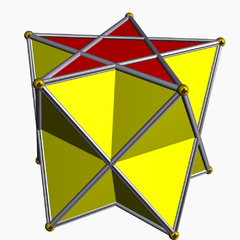
| Type | Prismatic uniform polyhedron |
| Elements | F = 12, E = 20 V = 10 (χ = 2) |
| Faces by sides | 10{3}+2{5/2} |
| Schläfli symbol | sr{2,5/2} |
| Wythoff symbol | | 2 2 5/2 |
| Coxeter diagram |     
|
| Symmetry | D5h, [5,2], (*552), order 20 |
| Rotation group | D5, [5,2]+, (55), order 10 |
| Index references | U79(a) |
| Dual | Pentagrammic trapezohedron |
| Properties | nonconvex |
 Vertex figure 3.3.3.5/2 | |
In geometry, the pentagrammic antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
It has 12 faces, 20 edges and 10 vertices. This polyhedron is identified with the indexed name U79 as a uniform polyhedron.[1]
Note that the pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior depending on how interior is defined. One definition of interior is the set of points that have a ray that crosses the boundary an odd number of times to escape the perimeter.
In either case, it is best to show the pentagram boundary line to distinguish it from a concave decagon.
Gallery
[edit] An alternative representation with hollow centers to the pentagrams.
|
 The pentagrammic trapezohedron is the dual to the pentagrammic antiprism.
|
Net
[edit]Net (fold the dotted line in the centre in the opposite direction to all the other lines):
See also
[edit]References
[edit]- ^ Maeder, Roman. "79: pentagrammic antiprism".
External links
[edit]- Weisstein, Eric W. "Pentagrammic antiprism". MathWorld.
- http://www.mathconsult.ch/showroom/unipoly/04.html
- https://web.archive.org/web/20050313233653/http://www.math.technion.ac.il/~rl/kaleido/data/04.html
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |