Component (graph theory): Difference between revisions
source strong connectivity |
source biconnected |
||
| Line 19: | Line 19: | ||
The [[equivalence class]]es of this relation partition the vertices of the graph into [[disjoint sets]], subsets of vertices that are all reachable from each other, with no additional reachable pairs outside of any of these subsets. Each vertex belongs to exactly one equivalence class. The components are then the [[induced subgraph]]s formed by each of these equivalence classes.{{r|foldes}} |
The [[equivalence class]]es of this relation partition the vertices of the graph into [[disjoint sets]], subsets of vertices that are all reachable from each other, with no additional reachable pairs outside of any of these subsets. Each vertex belongs to exactly one equivalence class. The components are then the [[induced subgraph]]s formed by each of these equivalence classes.{{r|foldes}} |
||
Similar definitions involving equivalence classes have been used to defined components for more advanced forms of graph [[Connectivity (graph theory)|connectivity]], including the [[strongly connected component]]s of [[directed graph]]s{{r|lewzax}} and the [[biconnected component]]s of undirected graphs. |
Similar definitions involving equivalence classes have been used to defined components for more advanced forms of graph [[Connectivity (graph theory)|connectivity]], including the [[strongly connected component]]s of [[directed graph]]s{{r|lewzax}} and the [[biconnected component]]s of undirected graphs.{{r|kozen}} |
||
==Number of components== |
==Number of components== |
||
| Line 162: | Line 162: | ||
| publisher = Google |
| publisher = Google |
||
| title = Algorithmic Graph Theory and Sage}}</ref> |
| title = Algorithmic Graph Theory and Sage}}</ref> |
||
<ref name=kozen>{{citation |
|||
| last = Kozen | first = Dexter C. | author-link = Dexter Kozen |
|||
| contribution = 4.1 Biconnected components |
|||
| contribution-url = https://books.google.com/books?id=HFn1BwAAQBAJ&pg=PA20 |
|||
| doi = 10.1007/978-1-4612-4400-4 |
|||
| isbn = 0-387-97687-6 |
|||
| mr = 1139767 |
|||
| pages = 20–22 |
|||
| publisher = Springer-Verlag | location = New York |
|||
| series = Texts and Monographs in Computer Science |
|||
| title = The Design and Analysis of Algorithms |
|||
| year = 1992}}</ref> |
|||
<ref name=lewpap>{{citation |
<ref name=lewpap>{{citation |
||
Revision as of 19:21, 8 January 2022

In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are also sometimes called connected components.
Definitions and examples
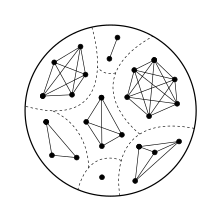
A component of a given undirected graph may be defined as a connected subgraph that is not part of any larger connected subgraph. Every vertex of a graph belongs to one of the graph's components, which may be found as the induced subgraph of the set of vertices reachable from .[1] Every graph is the disjoint union of its components.[2] For instance, the graph shown in the first illustration has three components. Additional examples of this general rule include the following special cases:
- In an empty graph, each vertex forms a component with one vertex and zero edges.[3] More generally a component of this type is formed for every isolated vertex in any graph.[4]
- In a connected graph, there is exactly one component, the whole graph.[4]
- In a forest, every component is a tree.
- In a cluster graph, every component is a maximal clique. These graphs may be produced as the transitive closures of arbitrary undirected graphs, for which finding the transitive closure is an equivalent formulation of identifying the connected components.[5]
Another way to define components involves the equivalence classes of an equivalence relation that is defined on the vertices of the graph. In an undirected graph, a vertex is reachable from a vertex if there is a path from to . In this definition, a single vertex is counted as a path of length zero, and the same vertex may occur more than once within a path. Reachability is an equivalence relation, since:
- It is reflexive: There is a trivial path of length zero from any vertex to itself.
- It is symmetric: If there is a path from to , the same edges in the reverse order form a path from to .
- It is transitive: If there is a path from to and a path from to , the two paths may be concatenated together to form a path from to .
The equivalence classes of this relation partition the vertices of the graph into disjoint sets, subsets of vertices that are all reachable from each other, with no additional reachable pairs outside of any of these subsets. Each vertex belongs to exactly one equivalence class. The components are then the induced subgraphs formed by each of these equivalence classes.[6]
Similar definitions involving equivalence classes have been used to defined components for more advanced forms of graph connectivity, including the strongly connected components of directed graphs[7] and the biconnected components of undirected graphs.[8]
Number of components
The number of components of a given graph can be used to count the number of edges in its spanning forests: in a graph with vertices and components, every spanning forest will have exactly edges. This number is the matroid-theoretic rank of the graph, and is the matroid rank of the graphic matroid associated with the graph. The rank of its dual matroid is the circuit rank of the graph, the minimum number of edges that must be removed from the graph to break all its cycles. In a graph with edges, vertices and components, the circuit rank is .
A graph can be interpreted as a topological space in multiple ways, for instance by placing its vertices as points in general position in three-dimensional Euclidean space and representing its edges as line segments between those points.[9] The components of a graph can be generalized through these interpretations as the number of topological connected components of the corresponding space. Just as the number of connected components is an important topological invariant, the zeroth Betti number of a space, the number of components of a graph is an important graph invariant, and in topological graph theory it can be interpreted as the zeroth Betti number of the graph.[3]
The same number arises in other ways in graph theory as well. In algebraic graph theory it equals the multiplicity of 0 as an eigenvalue of the Laplacian matrix of the graph.[10] It is also the index of the first nonzero coefficient of the chromatic polynomial of a graph, and the chromatic polynomial of the whole graph can be obtained as the product of the polynomials of its components.[11] Numbers of components play a key role in the Tutte theorem characterizing graphs that have perfect matchings[12] and the associated Tutte–Berge formula for the size of a maximum matching,[13] and in the definition of graph toughness.[14]
Algorithms
It is straightforward to compute the components of a graph in linear time (in terms of the numbers of the vertices and edges of the graph) using either breadth-first search or depth-first search. In either case, a search that begins at some particular vertex will find the entire component containing (and no more) before returning. To find all the components of a graph, loop through its vertices, starting a new breadth first or depth first search whenever the loop reaches a vertex that has not already been included in a previously found component. Hopcroft & Tarjan (1973) describe essentially this algorithm, and state that at that point it was already "well known".[15]
Connected-component labeling, a basic technique in computer image analysis, involves the construction of a graph from the image, in which the vertices are the subset of pixels of the image that meet some criterion for being included in a component, and the edges connect adjacent pixels (with adjacency defined either orthogonally according to the Von Neumann neighborhood, or both orthogonally and diagonally according to the Moore neighborhood). The connected components of this graph form objects, that can be subjected to additional processing. Researchers in this area have developed several component-finding algorithms specialized for this type of graph, allowing it to be processed in pixel order rather than in the more scattered order that would be generated by breadth-first or depth-first searching.[16]
There are also efficient algorithms to dynamically track the components of a graph as vertices and edges are added, by using a disjoint-set data structure to keep track of the partition of the vertices into equivalence classes, replacing any two classes by their union when an edge connecting them is added. These algorithms take amortized time per operation, where adding vertices and edges and determining the component in which a vertex falls are both operations, and is a very slowly growing inverse of the very quickly growing Ackermann function.[17] One application of this sort of incremental connectivity algorithm is in Kruskal's algorithm for minimum spanning trees, which adds edges to a graph in sorted order by length and includes an edge in the minimum spanning tree only when it connects two different components of the previously-added subgraph.[18] When both edge insertions and edge deletions are allowed, it is still possible to maintain the same information, in amortized time per change and time per connectivity query,[19] or in near-logarithmic randomized expected time.[20]
Components of graphs have been used in computational complexity theory to study the power of Turing machines that have a working memory limited to a logarithmic number of bits, with the much larger input accessible only through read access rather than being modifiable. The problems that can be solved by machines limited in this way define the complexity class L. It was unclear for many years whether connected components could be found in this model, when formalized as a decision problem of testing whether two vertices belong to the same component, and in 1982 a related complexity class, SL, was defined to include this connectivity problem and any other problem equivalent to it under logarithmic-space reductions.[21] Finally, in 2008, it was proven that this connectivity problem can be solved in logarithmic space, and therefore that SL = L.[22]
In random graphs
In random graphs the sizes of components are given by a random variable, which, in turn, depends on the specific model. In the version of the Erdős–Rényi model, a graph on vertices is generated by choosing randomly and independently for each pair of vertices whether to include an edge connecting that pair, with probability of including an edge and probability of leaving those two vertices without an edge connecting them. The connectivity of this model depends on , and there are three different ranges of with very different behavior from each other (with high probability):
- Subcritical
- In this range of , all components are simple and very small. The largest component has size . The graph is a pseudoforest, and most of its components are trees.
- Critical
- There is a single giant component with ; the remaining components are small, with size .
- Supercritical
- The size of the giant component becomes linear, and for large values of approaches the whole graph: where is the positive solution to the equation Again, all remaining components are small.
For a different model, the random subgraphs of grid graphs, the connected components are described by percolation theory.
References
- ^ Clark, John; Holton, Derek Allan (1995), A First Look at Graph Theory, Allied Publishers, p. 28, ISBN 9788170234630
- ^ Joyner, David; Nguyen, Minh Van; Phillips, David (May 10, 2013), "1.6.1 Union, intersection, and join", Algorithmic Graph Theory and Sage (0.8-r1991 ed.), Google, pp. 34–35
- ^ a b Tutte, W. T. (1984), Graph Theory, Encyclopedia of Mathematics and its Applications, vol. 21, Reading, Massachusetts: Addison-Wesley, p. 15, ISBN 0-201-13520-5, MR 0746795
- ^ a b Thulasiraman, K.; Swamy, M. N. S. (2011), Graphs: Theory and Algorithms, John Wiley & Sons, p. 9, ISBN 978-1-118-03025-7
- ^ McColl, W. F.; Noshita, K. (1986), "On the number of edges in the transitive closure of a graph", Discrete Applied Mathematics, 15 (1): 67–73, doi:10.1016/0166-218X(86)90020-X, MR 0856101
- ^ Foldes, Stephan (2011), Fundamental Structures of Algebra and Discrete Mathematics, John Wiley & Sons, p. 199, ISBN 978-1-118-03143-8
- ^ Lewis, Harry; Zax, Rachel (2019), Essential Discrete Mathematics for Computer Science, Princeton University Press, p. 145, ISBN 978-0-691-19061-7
- ^ Kozen, Dexter C. (1992), "4.1 Biconnected components", The Design and Analysis of Algorithms, Texts and Monographs in Computer Science, New York: Springer-Verlag, pp. 20–22, doi:10.1007/978-1-4612-4400-4, ISBN 0-387-97687-6, MR 1139767
- ^ Wood, David R. (2014), "Three-dimensional graph drawing", in Kao, Ming-Yang (ed.), Encyclopedia of Algorithms (PDF), Springer, pp. 1–7, doi:10.1007/978-3-642-27848-8_656-1
- ^ Cioabă, Sebastian M. (2011), "Some applications of eigenvalues of graphs", in Dehmer, Matthias (ed.), Structural Analysis of Complex Networks, New York: Birkhäuser/Springer, pp. 357–379, doi:10.1007/978-0-8176-4789-6_14, MR 2777924; see proof of Lemma 5, p. 361
- ^ Read, Ronald C. (1968), "An introduction to chromatic polynomials", Journal of Combinatorial Theory, 4: 52–71, doi:10.1016/S0021-9800(68)80087-0, MR 0224505; see Theorem 2, p. 59, and corollary, p. 65
- ^ Tutte, W. T. (1947), "The factorization of linear graphs", The Journal of the London Mathematical Society, 22: 107–111, doi:10.1112/jlms/s1-22.2.107, MR 0023048
- ^ Berge, Claude (1958), "Sur le couplage maximum d'un graphe", Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences, 247: 258–259, MR 0100850
- ^ Chvátal, Václav (1973), "Tough graphs and Hamiltonian circuits", Discrete Mathematics, 5 (3): 215–228, doi:10.1016/0012-365X(73)90138-6, MR 0316301
- ^ Hopcroft, John; Tarjan, Robert (June 1973), "Algorithm 447: efficient algorithms for graph manipulation", Communications of the ACM, 16 (6): 372–378, doi:10.1145/362248.362272
- ^ Dillencourt, Michael B.; Samet, Hanan; Tamminen, Markku (1992), "A general approach to connected-component labeling for arbitrary image representations", Journal of the ACM, 39 (2): 253–280, doi:10.1145/128749.128750, MR 1160258
- ^ Bengelloun, Safwan Abdelmajid (December 1982), Aspects of Incremental Computing (PhD thesis), Yale University, p. 12, ProQuest 303248045
- ^ Skiena, Steven (2008), "6.1.2 Kruskal's Algorithm", The Algorithm Design Manual, Springer, pp. 196–198, doi:10.1007/978-1-84800-070-4, ISBN 978-1-84800-069-8
- ^ Wulff-Nilsen, Christian (2013), "Faster deterministic fully-dynamic graph connectivity", in Khanna, Sanjeev (ed.), Proceedings of the Twenty-Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2013, New Orleans, Louisiana, USA, January 6-8, 2013, pp. 1757–1769, arXiv:1209.5608, doi:10.1137/1.9781611973105.126
- ^ Huang, Shang-En; Huang, Dawei; Kopelowitz, Tsvi; Pettie, Seth (2017), "Fully dynamic connectivity in amortized expected time", in Klein, Philip N. (ed.), Proceedings of the Twenty-Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, SODA 2017, Barcelona, Spain, Hotel Porta Fira, January 16-19, pp. 510–520, arXiv:1609.05867, doi:10.1137/1.9781611974782.32
- ^ Lewis, Harry R.; Papadimitriou, Christos H. (1982), "Symmetric space-bounded computation", Theoretical Computer Science, 19 (2): 161–187, doi:10.1016/0304-3975(82)90058-5, MR 0666539
- ^ Reingold, Omer (2008), "Undirected connectivity in log-space", Journal of the ACM, 55 (4): A17:1–A17:24, doi:10.1145/1391289.1391291, MR 2445014
External links
- MATLAB code to find components in undirected graphs, MATLAB File Exchange.
- Connected components, Steven Skiena, The Stony Brook Algorithm Repository
























