Triangular prism: Difference between revisions
Dedhert.Jr (talk | contribs) →Related polyhedron: explain more definition |
Dedhert.Jr (talk | contribs) sources |
||
| Line 29: | Line 29: | ||
== Related polyhedron == |
== Related polyhedron == |
||
Beyond the triangular bipyramid as its dual polyhedron, many other polyhedrons are related to the triangular prism. A [[Johnson solid]] is a convex polyhedron with regular faces, and this definition is sometimes omitted uniform polyhedrons such as [[Archmidean solid]]s, [[Catalan solid]]s, prisms and [[antiprism]]s. There are 5 Johnson solids with their construction involving the triangular prism: [[elongated triangular pyramid]], [[elongated triangular bipyramid]], [[augmented triangular prism]], [[biaugmented triangular prism]], and [[triaugmented triangular prism]]. The elongated triangular pyramid and the gyroelongated triangular pyramid are constructed by attaching [[tetrahedron]] onto the base of a triangular prism. The augmented triangular prism, augmented triangular prism, and triaugmented triangular prism are constructed by attaching [[equilateral square pyramid]]s onto the square face of the prism.{{sfnp|Rajwade|2001}} |
Beyond the triangular bipyramid as its dual polyhedron, many other polyhedrons are related to the triangular prism. A [[Johnson solid]] is a convex polyhedron with regular faces, and this definition is sometimes omitted uniform polyhedrons such as [[Archmidean solid]]s, [[Catalan solid]]s, prisms and [[antiprism]]s.<ref>{{reflist| |
||
{{harvp|Todesco|2020|p=[https://books.google.com/books?id=wtIBEAAAQBAJ&pg=PA282 282}}| |
|||
{{harvp|Williams|Monteleone|2021|p=[https://books.google.com/books?id=w5RBEAAAQBAJ&pg=PA23 23]}} |
|||
}}</ref> There are 5 Johnson solids with their construction involving the triangular prism: [[elongated triangular pyramid]], [[elongated triangular bipyramid]], [[augmented triangular prism]], [[biaugmented triangular prism]], and [[triaugmented triangular prism]]. The elongated triangular pyramid and the gyroelongated triangular pyramid are constructed by attaching [[tetrahedron]] onto the base of a triangular prism. The augmented triangular prism, augmented triangular prism, and triaugmented triangular prism are constructed by attaching [[equilateral square pyramid]]s onto the square face of the prism.{{sfnp|Rajwade|2001}} |
|||
[[File:TruncatedTriangularPrism.png|200px|thumb|Truncted right triangular prism]] |
[[File:TruncatedTriangularPrism.png|200px|thumb|Truncted right triangular prism]] |
||
| Line 224: | Line 227: | ||
| isbn = 978-93-86279-06-4 |
| isbn = 978-93-86279-06-4 |
||
| doi = 10.1007/978-93-86279-06-4 |
| doi = 10.1007/978-93-86279-06-4 |
||
}} |
|||
* {{cite book |
|||
| last = Todesco | first = Gian Marco |
|||
| editor-last1 = Emmer | editor-first1 = Michele |
|||
| editor-last2 = Abate | editor-first2 = Marco |
|||
| year = 2020 |
|||
| contribution = Hyperbolic Honeycomb |
|||
| title = Imagine Math 7: Between Culture and Mathematics |
|||
| publisher = Springer |
|||
| doi = 10.1007/978-3-030-42653-8 |
|||
| isbn = 978-3-030-42653-8 |
|||
}} |
|||
* {{cite book |
|||
| last1 = Williams | first1 = Kim |
|||
| last2 = Monteleone | first2 = Cosino |
|||
| year = 2021 |
|||
| title = Daniele Barbaro’s Perspective of 1568 |
|||
| publisher = Springer |
|||
| isbn = 978-3-030-76687-0 |
|||
| doi = 10.1007/978-3-030-76687-0 |
|||
}} |
}} |
||
{{refend}} |
{{refend}} |
||
Revision as of 05:56, 29 February 2024
| Triangular prism | |
|---|---|
 | |
| Type | Prism Semiregular polyhedron Uniform polyhedron |
| Faces | 5 |
| Edges | 9 |
| Vertices | 6 |
| Symmetry group | D3h |
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides; otherwise, it is oblique. A uniform triangular prism is a right triangular prism with equilateral bases and square sides.
Equivalently, it is a polyhedron in which two faces are parallel, while the surface normals of the other three are in the same plane (which is not necessarily parallel to the base planes). These three faces are parallelograms. All cross-sections parallel to the base faces are the same triangle.
Properties
A triangular prism has 6 edges, 9 edges, and 5 faces. A prism has 2 faces, known as the base of a prism, and the bases of a triangular prism are triangles. The triangle has 3 vertices, each of which pairs with another triangle's vertex, making up another 3 edges. These edges form a 3 rectangles as other faces.[1] If the prism's edges are perpendicular to the base, the prism is called a right triangular prism.[2]

If the base becomes equilateral and the rest of its faces becomes square, then the right triangular prism is semiregular. A semiregular prism means that the number of its polygonal base's edges equals the number of its square faces.[3] More generally, the triangular prism is uniform. This means that a triangular prism has regular faces and has an isogonal symmetry on vertices.[4] The symmetry group of a right triangular prism is dihedral group D3h of order 12: the appearance is unchanged if the triangular prism is rotated one- and two- thirds of a full angle around its axis of symmetry passing through the center's base, and reflecting across a horizontal plane. The dual polyhedron of a triangular prism is a triangular bipyramid. The triangular bipyramid has the same symmetry as the triangular prism.[1] The dihedral angle between two adjacent square faces is the internal angle of an equilateral triangle π/3 = 60°, and that between square-to-triangle is π/2 = 90°.[5]
The volume of any prism is the product of the area of the base and the distance between the two bases.[6] In the case of a triangular prism, its base is a triangle, so its volume can be calculated by multiplying the area of a triangle and the length of the prism: where b is the length of one side of the triangle, h is the length of an altitude drawn to that side, and l is the distance between the triangular faces.[7]
Related polyhedron
Beyond the triangular bipyramid as its dual polyhedron, many other polyhedrons are related to the triangular prism. A Johnson solid is a convex polyhedron with regular faces, and this definition is sometimes omitted uniform polyhedrons such as Archmidean solids, Catalan solids, prisms and antiprisms.[8] There are 5 Johnson solids with their construction involving the triangular prism: elongated triangular pyramid, elongated triangular bipyramid, augmented triangular prism, biaugmented triangular prism, and triaugmented triangular prism. The elongated triangular pyramid and the gyroelongated triangular pyramid are constructed by attaching tetrahedron onto the base of a triangular prism. The augmented triangular prism, augmented triangular prism, and triaugmented triangular prism are constructed by attaching equilateral square pyramids onto the square face of the prism.[9]

A truncated right triangular prism is a triangular prism constructed by truncating its part at an oblique angle. As a result, this prism has different length edges. Given that A is one base triangular prism, and the three heights h1, h2, and h3, its volume can be determined by in the following formula:[10]
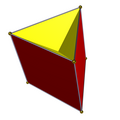
Facetings
There are two full D3h symmetry facetings of a triangular prism, both with 6 isosceles triangle faces, one keeping the original top and bottom triangles, and one the original squares. Two lower C3v symmetry facetings have one base triangle, 3 lateral crossed square faces, and 3 isosceles triangle lateral faces.
| Convex | Facetings | |||
|---|---|---|---|---|
| D3h symmetry | C3v symmetry | |||

|
|

|

|
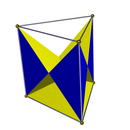
|
| 2 {3} 3 {4} |
3 {4} 6 ( ) v { } |
2 {3} 6 ( ) v { } |
1 {3} 3 t'{2} 6 ( ) v { } |
1 {3} 3 t'{2} 3 ( ) v { } |
Compounds
There are 4 uniform compounds of triangular prisms:
- Compound of four triangular prisms, compound of eight triangular prisms, compound of ten triangular prisms, compound of twenty triangular prisms.
Honeycombs
There are 9 uniform honeycombs that include triangular prism cells:
- Gyroelongated alternated cubic honeycomb, elongated alternated cubic honeycomb, gyrated triangular prismatic honeycomb, snub square prismatic honeycomb, triangular prismatic honeycomb, triangular-hexagonal prismatic honeycomb, truncated hexagonal prismatic honeycomb, rhombitriangular-hexagonal prismatic honeycomb, snub triangular-hexagonal prismatic honeycomb, elongated triangular prismatic honeycomb
Related polytopes
The triangular prism is first in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes (equilateral triangles and squares in the case of the triangular prism). In Coxeter's notation the triangular prism is given the symbol −121.
| k21 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 1,920 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph | 
|

|

|

|

|

|
- | - | |||
| Name | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
Four dimensional space
The triangular prism exists as cells of a number of four-dimensional uniform 4-polytopes, including:
See also
References
Citations
- ^ a b King (1994), p. 113.
- ^ Kern & Bland (1938), p. 25.
- ^ O'Keeffe & Hyde (2020), p. 139.
- ^
- ^ Johnson (1966).
- ^ Kern & Bland (1938), p. 26.
- ^ Kinsley, Moore & Parados (2011), p. 389.
- ^ <references></references>
- ^ Rajwade (2001).
- ^ Kern & Bland (1938), p. 81.
Bibilography
- Berman, Leah Wrenn; Williams, Gordon (2009). "Exploring Polyhedra and Discovering Euler's Formula". In Hopkin, Brian (ed.). Resources for Teaching Discrete Mathematics: Classroom Projects, History Modules, and Articles. Mathematical Association of America.
- Kern, William F.; Bland, James R. (1938). Solid Mensuration with proofs. OCLC 1035479.
- King, Robert B. (1994). "Polyhedral Dynamics". In Bonchev, Danail D.; Mekenyan, O.G. (eds.). Graph Theoretical Approaches to Chemical Reactivity. Springer. doi:10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
- Kinsey, L. Christine; Moore, Teresa E.; Prassidis, Efstratios (2011). Geometry and Symmetry. John Wiley & Sons. ISBN 978-0-470-49949-8.
- Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
- Messer, Peter W. (2002). "Closed-Form Expressions for Uniform Polyhedra and Their Duals". Discrete Comput Geometry. 27: 353–375. doi:10.1007/s00454-001-0078-2.
- O'Keeffe, Michael; Hyde, Bruce G. (2020). Crystal Structures: Patterns and Symmetry. Dover Publications. ISBN 978-0-486-83654-6.
- Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- Todesco, Gian Marco (2020). "Hyperbolic Honeycomb". In Emmer, Michele; Abate, Marco (eds.). Imagine Math 7: Between Culture and Mathematics. Springer. doi:10.1007/978-3-030-42653-8. ISBN 978-3-030-42653-8.
- Williams, Kim; Monteleone, Cosino (2021). Daniele Barbaro’s Perspective of 1568. Springer. doi:10.1007/978-3-030-76687-0. ISBN 978-3-030-76687-0.