Truncation (geometry)
 Truncated square is a regular octagon: t{4} = {8} |
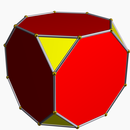 Truncated cube t{4,3} or |
 Truncated cubic honeycomb t{4,3,4} or |
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.
Uniform truncation[edit]
In general any polyhedron (or polytope) can also be truncated with a degree of freedom as to how deep the cut is, as shown in Conway polyhedron notation truncation operation.
A special kind of truncation, usually implied, is a uniform truncation, a truncation operator applied to a regular polyhedron (or regular polytope) which creates a resulting uniform polyhedron (uniform polytope) with equal edge lengths. There are no degrees of freedom, and it represents a fixed geometric, just like the regular polyhedra.
In general all single ringed uniform polytopes have a uniform truncation. For example, the icosidodecahedron, represented as Schläfli symbols r{5,3} or , and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]() or
or ![]()
![]()
![]() has a uniform truncation, the truncated icosidodecahedron, represented as tr{5,3} or ,
has a uniform truncation, the truncated icosidodecahedron, represented as tr{5,3} or , ![]()
![]()
![]() . In the Coxeter-Dynkin diagram, the effect of a truncation is to ring all the nodes adjacent to the ringed node.
. In the Coxeter-Dynkin diagram, the effect of a truncation is to ring all the nodes adjacent to the ringed node.
A uniform truncation performed on the regular triangular tiling {3,6} results in the regular hexagonal tiling {6,3}.
Truncation of polygons[edit]
A truncated n-sided polygon will have 2n sides (edges). A regular polygon uniformly truncated will become another regular polygon: t{n} is {2n}. A complete truncation (or rectification), r{3}, is another regular polygon in its dual position.
A regular polygon can also be represented by its Coxeter-Dynkin diagram, ![]()
![]()
![]() , and its uniform truncation
, and its uniform truncation ![]()
![]()
![]() , and its complete truncation
, and its complete truncation ![]()
![]()
![]() . The graph
. The graph ![]()
![]()
![]() represents Coxeter group I2(n), with each node representing a mirror, and the edge representing the angle π/n between the mirrors, and a circle is given around one or both mirrors to show which ones are active.
represents Coxeter group I2(n), with each node representing a mirror, and the edge representing the angle π/n between the mirrors, and a circle is given around one or both mirrors to show which ones are active.
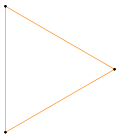 {3} |

|
 t{3} = {6} |

|
 r{3} = {3} |
Star polygons can also be truncated. A truncated pentagram {5/2} will look like a pentagon, but is actually a double-covered (degenerate) decagon ({10/2}) with two sets of overlapping vertices and edges. A truncated great heptagram {7/3} gives a tetradecagram {14/3}.
Uniform truncation in regular polyhedra and tilings and higher[edit]

When "truncation" applies to platonic solids or regular tilings, usually "uniform truncation" is implied, which means truncating until the original faces become regular polygons with twice as many sides as the original form.
This sequence shows an example of the truncation of a cube, using four steps of a continuous truncating process between a full cube and a rectified cube. The final polyhedron is a cuboctahedron. The middle image is the uniform truncated cube; it is represented by a Schläfli symbol t{p,q,...}.
A bitruncation is a deeper truncation, removing all the original edges, but leaving an interior part of the original faces. Example: a truncated octahedron is a bitruncated cube: t{3,4} = 2t{4,3}.
A complete bitruncation, called a birectification, reduces original faces to points. For polyhedra, this becomes the dual polyhedron. Example: an octahedron is a birectification of a cube: {3,4} = 2r{4,3}.
Another type of truncation, cantellation, cuts edges and vertices, removing the original edges, replacing them with rectangles, removing the original vertices, and replacing them with the faces of the dual of the original regular polyhedra or tiling.
Higher dimensional polytopes have higher truncations. Runcination cuts faces, edges, and vertices. In 5 dimensions, sterication cuts cells, faces, and edges.
Edge-truncation[edit]
Edge-truncation is a beveling, or chamfer for polyhedra, similar to cantellation, but retaining the original vertices, and replacing edges by hexagons. In 4-polytopes, edge-truncation replaces edges with elongated bipyramid cells.
Alternation or partial truncation[edit]
Alternation or partial truncation removes only some of the original vertices.
In partial truncation, or alternation, half of the vertices and connecting edges are completely removed. The operation applies only to polytopes with even-sided faces. Faces are reduced to half as many sides, and square faces degenerate into edges. For example, the tetrahedron is an alternated cube, h{4,3}.
Diminishment is a more general term used in reference to Johnson solids for the removal of one or more vertices, edges, or faces of a polytope, without disturbing the other vertices. For example, the tridiminished icosahedron starts with a regular icosahedron with 3 vertices removed.
Other partial truncations are symmetry-based; for example, the tetrahedrally diminished dodecahedron.
Generalized truncations[edit]

The linear truncation process can be generalized by allowing parametric truncations that are negative, or that go beyond the midpoint of the edges, causing self-intersecting star polyhedra, and can parametrically relate to some of the regular star polygons and uniform star polyhedra.
- Shallow truncation - Edges are reduced in length, faces are truncated to have twice as many sides, while new facets are formed, centered at the old vertices.
- Uniform truncation are a special case of this with equal edge lengths. The truncated cube, t{4,3}, with square faces becoming octagons, with new triangular faces are the vertices.
- Antitruncation A reverse shallow truncation, truncated outwards off the original edges, rather than inward. This results in a polytope which looks like the original, but has parts of the dual dangling off its corners, instead of the dual cutting into its own corners.
- Complete truncation or rectification - The limit of a shallow truncation, where edges are reduced to points. The cuboctahedron, r{4,3}, is an example.
- Hypertruncation A form of truncation that goes past the rectification, inverting the original edges, and causing self-intersections to appear.
- Quasitruncation A form of truncation that goes even farther than hypertruncation where the inverted edge becomes longer than the original edge. It can be generated from the original polytope by treating all the faces as retrograde, i.e. going backwards round the vertex. For example, quasitruncating the square gives a regular octagram (t{4,3}={8/3}), and quasitruncating the cube gives the uniform stellated truncated hexahedron, t{4/3,3}.
 ⇨ taC |
 Cube {4,3} C |
 ⇨ tC |
 Truncation t{4,3} tC |
 ⇨ tC |
 Complete truncation r{4,3} aC |
 ⇩ thC |
 Antitruncation taC |
 Hypertruncation thC | |||||
 ⇧ taC |
 Complete quasitruncation aqC |
 ⇦ |
 Quasitruncation t{4/3,3} tqC |
 ⇦ tqC |
 Complete hypertruncation ahC |
 ⇦ thC |
See also[edit]
- Uniform polyhedron
- Uniform 4-polytope
- Bitruncation (geometry)
- Rectification (geometry)
- Alternation (geometry)
- Conway polyhedron notation
- Truncated cone
References[edit]
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (pp. 145–154 Chapter 8: Truncation)
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
External links[edit]
- Weisstein, Eric W. "Truncation". MathWorld.
- Olshevsky, George. "Truncation". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polyhedra Names, truncation
| Seed | Truncation | Rectification | Bitruncation | Dual | Expansion | Omnitruncation | Alternations | ||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

| |||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |










