Center of curvature
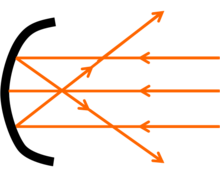
In geometry, the center of curvature of a curve is a point located at a distance from the curve equal to the radius of curvature lying on the curve normal vector.[1] It is the point at infinity if the curvature is zero. The osculating circle to the curve is centered at the centre of curvature. Cauchy defined the center of curvature C as the intersection point of two infinitely close normal lines to the curve.[2] The locus of centers of curvature for each point on the curve comprise the evolute of the curve. This term is generally used in physics regarding the study of lenses and mirrors (see radius of curvature (optics)).
It lies on the principal axis of a mirror or lens.[3] In case of a convex mirror it lies behind the polished, or reflecting, surface and it lies in front of the reflecting surface in case of a concave mirror.[4]
See also
[edit]References
[edit]- ^ Hilbert, David; Cohn-Vossen, Stephan (1952), Geometry and the Imagination, New York: Chelsea, p. 176
- ^ Borovik, Alexandre; Katz, Mikhail G. (2011), "Who gave you the Cauchy--Weierstrass tale? The dual history of rigorous calculus", Foundations of Science, 17 (3): 245–276, arXiv:1108.2885, doi:10.1007/s10699-011-9235-x, S2CID 119320059
- ^ "principal axis", Merriam-Webster.com Dictionary, Merriam-Webster, OCLC 1032680871, retrieved 15 December 2024
- ^ Humanic, Thomas J., "Chapter 23 The Reflection of Light: Mirrors" (PDF), Physics 1201 Electricity, Magnetism and Modern Physics, The Ohio State University, p. 11, retrieved 15 December 2024
 | This differential geometry-related article is a stub. You can help Wikipedia by adding missing information. |
 | This physics-related article is a stub. You can help Wikipedia by adding missing information. |