Cross section (physics)
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (January 2022) |
In physics, the cross section is a measure of the probability that a specific process will take place in a collision of two particles. For example, the Rutherford cross-section is a measure of probability that an alpha particle will be deflected by a given angle during an interaction with an atomic nucleus. Cross section is typically denoted σ (sigma) and is expressed in units of area, more specifically in barns. In a way, it can be thought of as the size of the object that the excitation must hit in order for the process to occur, but more exactly, it is a parameter of a stochastic process.
When two discrete particles interact in classical physics, their mutual cross section is the area transverse to their relative motion within which they must meet in order to scatter from each other. If the particles are hard inelastic spheres that interact only upon contact, their scattering cross section is related to their geometric size. If the particles interact through some action-at-a-distance force, such as electromagnetism or gravity, their scattering cross section is generally larger than their geometric size.
When a cross section is specified as the differential limit of a function of some final-state variable, such as particle angle or energy, it is called a differential cross section (see detailed discussion below). When a cross section is integrated over all scattering angles (and possibly other variables), it is called a total cross section or integrated total cross section. For example, in Rayleigh scattering, the intensity scattered at the forward and backward angles is greater than the intensity scattered sideways, so the forward differential scattering cross section is greater than the perpendicular differential cross section, and by adding all of the infinitesimal cross sections over the whole range of angles with integral calculus, we can find the total cross section.
Scattering cross sections may be defined in nuclear, atomic, and particle physics for collisions of accelerated beams of one type of particle with targets (either stationary or moving) of a second type of particle. The probability for any given reaction to occur is in proportion to its cross section. Thus, specifying the cross section for a given reaction is a proxy for stating the probability that a given scattering process will occur.
The measured reaction rate of a given process depends strongly on experimental variables such as the density of the target material, the intensity of the beam, the detection efficiency of the apparatus, or the angle setting of the detection apparatus. However, these quantities can be factored away, allowing measurement of the underlying two-particle collisional cross section.
Differential and total scattering cross sections are among the most important measurable quantities in nuclear, atomic, and particle physics.
With light scattering off of a particle, the cross section specifies the amount of optical power scattered from light of a given irradiance (power per area). It is important to note that although the cross section has the same units as area, the cross section may not necessarily correspond to the actual physical size of the target given by other forms of measurement. It is not uncommon for the actual cross-sectional area of a scattering object to be much larger or smaller than the cross section relative to some physical process. For example, plasmonic nanoparticles can have light scattering cross sections for particular frequencies that are much larger than their actual cross-sectional areas.
Collision among gas particles[edit]
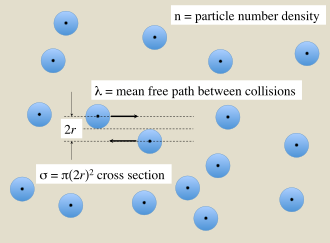
In a gas of finite-sized particles there are collisions among particles that depend on their cross-sectional size. The average distance that a particle travels between collisions depends on the density of gas particles. These quantities are related by
where
- σ is the cross section of a two-particle collision (SI units: m2),
- λ is the mean free path between collisions (SI units: m),
- n is the number density of the target particles (SI units: m−3).
If the particles in the gas can be treated as hard spheres of radius r that interact by direct contact, as illustrated in Figure 1, then the effective cross section for the collision of a pair is
If the particles in the gas interact by a force with a larger range than their physical size, then the cross section is a larger effective area that may depend on a variety of variables such as the energy of the particles.
Cross sections can be computed for atomic collisions but also are used in the subatomic realm. For example, in nuclear physics a "gas" of low-energy neutrons collides with nuclei in a reactor or other nuclear device, with a cross section that is energy-dependent and hence also with well-defined mean free path between collisions.
Attenuation of a beam of particles[edit]
If a beam of particles enters a thin layer of material of thickness dz, the flux Φ of the beam will decrease by dΦ according to
where σ is the total cross section of all events, including scattering, absorption, or transformation to another species. The volumetric number density of scattering centers is designated by n. Solving this equation exhibits the exponential attenuation of the beam intensity:
where Φ0 is the initial flux, and z is the total thickness of the material. For light, this is called the Beer–Lambert law.
Differential cross section[edit]
Consider a classical measurement where a single particle is scattered off a single stationary target particle. Conventionally, a spherical coordinate system is used, with the target placed at the origin and the z axis of this coordinate system aligned with the incident beam. The angle θ is the scattering angle, measured between the incident beam and the scattered beam, and the φ is the azimuthal angle.
The impact parameter b is the perpendicular offset of the trajectory of the incoming particle, and the outgoing particle emerges at an angle θ. For a given interaction (Coulombic, magnetic, gravitational, contact, etc.), the impact parameter and the scattering angle have a definite one-to-one functional dependence on each other. Generally the impact parameter can neither be controlled nor measured from event to event and is assumed to take all possible values when averaging over many scattering events. The differential size of the cross section is the area element in the plane of the impact parameter, i.e. dσ = b dφ db. The differential angular range of the scattered particle at angle θ is the solid angle element dΩ = sin θ dθ dφ. The differential cross section is the quotient of these quantities, dσ/dΩ.
It is a function of the scattering angle (and therefore also the impact parameter), plus other observables such as the momentum of the incoming particle. The differential cross section is always taken to be positive, even though larger impact parameters generally produce less deflection. In cylindrically symmetric situations (about the beam axis), the azimuthal angle φ is not changed by the scattering process, and the differential cross section can be written as
- .
In situations where the scattering process is not azimuthally symmetric, such as when the beam or target particles possess magnetic moments oriented perpendicular to the beam axis, the differential cross section must also be expressed as a function of the azimuthal angle.
For scattering of particles of incident flux Finc off a stationary target consisting of many particles, the differential cross section dσ/dΩ at an angle (θ,φ) is related to the flux of scattered particle detection Fout(θ,φ) in particles per unit time by
Here ΔΩ is the finite angular size of the detector (SI unit: sr), n is the number density of the target particles (SI units: m−3), and t is the thickness of the stationary target (SI units: m). This formula assumes that the target is thin enough that each beam particle will interact with at most one target particle.
The total cross section σ may be recovered by integrating the differential cross section dσ/dΩ over the full solid angle (4π steradians):
It is common to omit the “differential” qualifier when the type of cross section can be inferred from context. In this case, σ may be referred to as the integral cross section or total cross section. The latter term may be confusing in contexts where multiple events are involved, since “total” can also refer to the sum of cross sections over all events.
The differential cross section is extremely useful quantity in many fields of physics, as measuring it can reveal a great amount of information about the internal structure of the target particles. For example, the differential cross section of Rutherford scattering provided strong evidence for the existence of the atomic nucleus.
Instead of the solid angle, the momentum transfer may be used as the independent variable of differential cross sections.
Differential cross sections in inelastic scattering contain resonance peaks that indicate the creation of metastable states and contain information about their energy and lifetime.
Quantum scattering[edit]
In the time-independent formalism of quantum scattering, the initial wave function (before scattering) is taken to be a plane wave with definite momentum k:
where z and r are the relative coordinates between the projectile and the target. The arrow indicates that this only describes the asymptotic behavior of the wave function when the projectile and target are too far apart for the interaction to have any effect.
After scattering takes place it is expected that the wave function takes on the following asymptotic form:
where f is some function of the angular coordinates known as the scattering amplitude. This general form is valid for any short-ranged, energy-conserving interaction. It is not true for long-ranged interactions, so there are additional complications when dealing with electromagnetic interactions.
The full wave function of the system behaves asymptotically as the sum
The differential cross section is related to the scattering amplitude:
This has the simple interpretation as the probability density for finding the scattered projectile at a given angle.
A cross section is therefore a measure of the effective surface area seen by the impinging particles, and as such is expressed in units of area. The cross section of two particles (i.e. observed when the two particles are colliding with each other) is a measure of the interaction event between the two particles. The cross section is proportional to the probability that an interaction will occur; for example in a simple scattering experiment the number of particles scattered per unit of time (current of scattered particles Ir) depends only on the number of incident particles per unit of time (current of incident particles Ii), the characteristics of target (for example the number of particles per unit of surface N), and the type of interaction. For Nσ ≪ 1 we have
Relation to the S-matrix[edit]
If the reduced masses and momenta of the colliding system are mi, pi and mf, pf before and after the collision respectively, the differential cross section is given by[clarification needed]
where the on-shell T matrix is defined by
in terms of the S-matrix. Here δ is the Dirac delta function. The computation of the S-matrix is the main goal of the scattering theory.
Units[edit]
Although the SI unit of total cross sections is m2, smaller units are usually used in practice.
In nuclear and particle physics, the conventional unit is the barn b, where 1 b = 10−28 m2 = 100 fm2.[1] Smaller prefixed units such as mb and μb are also widely used. Correspondingly, the differential cross section can be measured in units such as mb/sr.
When the scattered radiation is visible light, it is conventional to measure the path length in centimetres. To avoid the need for conversion factors, the scattering cross section is expressed in cm2, and the number concentration in cm−3. The measurement of the scattering of visible light is known as nephelometry, and is effective for particles of 2–50 μm in diameter: as such, it is widely used in meteorology and in the measurement of atmospheric pollution.
The scattering of X-rays can also be described in terms of scattering cross sections, in which case the square ångström is a convenient unit: 1 Å2 = 10−20 m2 = 10000 pm2 = 108 b. The sum of the scattering, photoelectric, and pair-production cross-sections (in barns) is charted as the "atomic attenuation coefficient" (narrow-beam), in barns.[2]
Scattering of light[edit]
For light, as in other settings, the scattering cross section for particles is generally different from the geometrical cross section of the particle, and it depends upon the wavelength of light and the permittivity, shape, and size of the particle. The total amount of scattering in a sparse medium is proportional to the product of the scattering cross section and the number of particles present.
In the interaction of light with particles, many processes occur, each with their own cross sections, including absorption, scattering, and photoluminescence. The sum of the absorption and scattering cross sections is sometimes referred to as the attenuation or extinction cross section.
The total extinction cross section is related to the attenuation of the light intensity through the Beer–Lambert law, which says that attenuation is proportional to particle concentration:
where Aλ is the attenuation at a given wavelength λ, C is the particle concentration as a number density, and l is the path length. The absorbance of the radiation is the logarithm (decadic or, more usually, natural) of the reciprocal of the transmittance T:[3]
Combining the scattering and absorption cross sections in this manner is often necessitated by the inability to distinguish them experimentally, and much research effort has been put into developing models that allow them to be distinguished, the Kubelka-Munk theory being one of the most important in this area.
Cross section and Mie theory[edit]
Cross sections commonly calculated using Mie theory include efficiency coefficients for extinction , scattering , and Absorption cross sections. These are normalized by the geometrical cross sections of the particle as
where is the energy flow through the surrounding surface, and is the intensity of the incident wave. For a plane wave the intensity is going to be , where is the impedance of the host medium.
The main approach is based on the following. Firstly, we construct an imaginary sphere of radius (surface ) around the particle (the scatterer). The net rate of electromagnetic energy crosses the surface is
where is the time averaged Poynting vector. If energy is absorbed within the sphere, otherwise energy is being created within the sphere. We will not consider this case here. If the host medium is non-absorbing, the energy must be absorbed by the particle. We decompose the total field into incident and scattered parts , and the same for the magnetic field . Thus, we can decompose into the three terms , where
Where , , and .
All the field can be decomposed into the series of vector spherical harmonics (VSH). After that, all the integrals can be taken. In the case of a uniform sphere of radius , permittivity , and permeability the problem has a precise solution.[4] The scattering and extinction coefficients are
Dipole approximation for the scattering cross section[edit]
Let us assume that a particle supports only electric and magnetic dipole modes with polarizabilities and (here we use the notation of magnetic polarizability in the manner of Bekshaev et al.[5][6] rather than the notation of Nieto-Vesperinas et al.[7]) expressed through the Mie coefficients as
For the case of a no-inside-gain particle, i.e. no energy is emitted by the particle internally (), we have a particular case of the Optical theorem
Scattering of light on extended bodies[edit]
In the context of scattering light on extended bodies, the scattering cross section, σsc, describes the likelihood of light being scattered by a macroscopic particle. In general, the scattering cross section is different from the geometrical cross section of a particle, as it depends upon the wavelength of light and the permittivity in addition to the shape and size of the particle. The total amount of scattering in a sparse medium is determined by the product of the scattering cross section and the number of particles present. In terms of area, the total cross section (σ) is the sum of the cross sections due to absorption, scattering, and luminescence:
The total cross section is related to the absorbance of the light intensity through the Beer–Lambert law, which says that absorbance is proportional to concentration: Aλ = Clσ, where Aλ is the absorbance at a given wavelength λ, C is the concentration as a number density, and l is the path length. The extinction or absorbance of the radiation is the logarithm (decadic or, more usually, natural) of the reciprocal of the transmittance T:[3]
Relation to physical size[edit]
There is no simple relationship between the scattering cross section and the physical size of the particles, as the scattering cross section depends on the wavelength of radiation used. This can be seen when looking at a halo surrounding the Moon on a decently foggy evening: Red light photons experience a larger cross sectional area of water droplets than photons of higher energy. The halo around the Moon thus has a perimeter of red light due to lower energy photons being scattering further from the center of the Moon. Photons from the rest of the visible spectrum are left within the center of the halo and perceived as white light.
Meteorological range[edit]
The scattering cross section is related to the meteorological range LV:
The quantity Cσscat is sometimes denoted bscat, the scattering coefficient per unit length.[8]
Examples[edit]
Elastic collision of two hard spheres[edit]
The following equations apply to two hard spheres that undergo a perfectly elastic collision.[9] Let R and r denote the radii of the scattering center and scattered sphere, respectively. The differential cross section is
and the total cross section is
In other words, the total scattering cross section is equal to the area of the circle (with radius r + R) within which the center of mass of the incoming sphere has to arrive for it to be deflected.
Rutherford scattering[edit]
In Rutherford scattering, an incident particle with charge q and energy E scatters off a fixed particle with charge Q. The differential cross section is
where is the Coulomb constant.[10] The total cross section is infinite unless a cutoff for small scattering angles is applied.[11] This is due to the long range of the Coulomb potential.
Scattering from a 2D circular mirror[edit]
The following example deals with a beam of light scattering off a circle with radius r and a perfectly reflecting boundary. The beam consists of a uniform density of parallel rays, and the beam-circle interaction is modeled within the framework of geometric optics. Because the problem is genuinely two-dimensional, the cross section has units of length (e.g., meters). Let α be the angle between the light ray and the radius joining the reflection point of the ray with the center point of the mirror. Then the increase of the length element perpendicular to the beam is
The reflection angle of this ray with respect to the incoming ray is 2α, and the scattering angle is
The differential relationship between incident and reflected intensity I is
The differential cross section is therefore (dΩ = dθ)
Its maximum at θ = π corresponds to backward scattering, and its minimum at θ = 0 corresponds to scattering from the edge of the circle directly forward. This expression confirms the intuitive expectations that the mirror circle acts like a diverging lens. The total cross section is equal to the diameter of the circle:
Scattering from a 3D spherical mirror[edit]
The result from the previous example can be used to solve the analogous problem in three dimensions, i.e., scattering from a perfectly reflecting sphere of radius a.
The plane perpendicular to the incoming light beam can be parameterized by cylindrical coordinates r and φ. In any plane of the incoming and the reflected ray we can write (from the previous example):
while the impact area element is
In spherical coordinates,
Together with the trigonometric identity
we obtain
The total cross section is
See also[edit]
- Cross section (geometry)
- Flow velocity
- Luminosity (scattering theory)
- Linear attenuation coefficient
- Mass attenuation coefficient
- Neutron cross section
- Nuclear cross section
- Gamma ray cross section
- Partial wave analysis
- Particle detector
- Radar cross-section
- Rutherford scattering
- Scattering amplitude
References[edit]
- ^ International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), pp. 127–28, ISBN 92-822-2213-6, archived (PDF) from the original on 2021-06-04, retrieved 2021-12-16
- ^ Nondestructive Testing Handbook Volume 4 Radiographic Testing, ASNT, 2002, chapter 22.
- ^ a b Bajpai, P. K. (2008). Biological instrumentation and methodology (Revised 2nd ed.). Ram Nagar, New Delhi: S. Chand & Company Ltd. ISBN 9788121926331. OCLC 943495167.
- ^ Bohren, Craig F., and Donald R. Huffman. Absorption and scattering of light by small particles. John Wiley & Sons, 2008.
- ^ Bekshaev, A Ya (2013-04-01). "Subwavelength particles in an inhomogeneous light field: optical forces associated with the spin and orbital energy flows". Journal of Optics. 15 (4): 044004. arXiv:1210.5730. Bibcode:2013JOpt...15d4004B. doi:10.1088/2040-8978/15/4/044004. ISSN 2040-8978. S2CID 119234614.
- ^ Bliokh, Konstantin Y.; Bekshaev, Aleksandr Y.; Nori, Franco (2014-03-06). "Extraordinary momentum and spin in evanescent waves". Nature Communications. 5 (1). Springer Science and Business Media LLC: 3300. arXiv:1308.0547. Bibcode:2014NatCo...5.3300B. doi:10.1038/ncomms4300. ISSN 2041-1723. PMID 24598730. S2CID 15832637.
- ^ Nieto-Vesperinas, M.; Sáenz, J. J.; Gómez-Medina, R.; Chantada, L. (2010-05-14). "Optical forces on small magnetodielectric particle". Optics Express. 18 (11). The Optical Society: 11428–11443. Bibcode:2010OExpr..1811428N. doi:10.1364/oe.18.011428. ISSN 1094-4087. PMID 20589003.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Scattering cross section, σscat". doi:10.1351/goldbook.S05490
- ^ Taylor 2005, pp. 564, 574.
- ^ Taylor 2005, p. 576.
- ^ Griffiths 2005, p. 409.
Bibliography[edit]
- Griffiths, David J. (2005). Introduction to quantum mechanics. Pearson Prentice Hall. ISBN 0-13-111892-7. OCLC 53926857.
- Taylor, John R. (2005). Classical mechanics. Mill Valley, California. ISBN 1-891389-22-X. OCLC 55729992.
{{cite book}}: CS1 maint: location missing publisher (link) - J. D. Bjorken, S. D. Drell, Relativistic Quantum Mechanics, 1964
- P. Roman, Introduction to Quantum Theory, 1969
- W. Greiner, J. Reinhardt, Quantum Electrodynamics, 1994
- R. G. Newton. Scattering Theory of Waves and Particles. McGraw Hill, 1966.
- R. C. Fernow (1989). Introduction to Experimental Particle Physics. Cambridge University Press. ISBN 978-0-521-379-403.
External links[edit]
- Nuclear Cross Section
- Scattering Cross Section
- IAEA - Nuclear Data Services
- BNL - National Nuclear Data Center
- Particle Data Group - The Review of Particle Physics
- IUPAC Goldbook - Definition: Reaction Cross Section
- IUPAC Goldbook - Definition: Collision Cross Section
- ShimPlotWell cross section plotter for nuclear data

























![{\displaystyle \left[W_{\alpha }\right]=\left[{\text{W}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9af979c3f12fb9f318f5208c1a33b54c5b4b7c5)
![{\displaystyle \left[I_{\text{inc}}\right]=\left[{\frac {\text{W}}{{\text{m}}^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/980299cc5ada8a167bca66d7234045bc815d47b2)





![{\displaystyle \mathbf {\Pi } ={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} ^{*}\times \mathbf {H} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f07ff7f482d858e82afe9210c73cdf3d201aff9)






![{\displaystyle \mathbf {\Pi } _{i}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{i}^{*}\times \mathbf {H} _{i}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/858e7669298f797a2182b4ccd742d2330fe32f75)
![{\displaystyle \mathbf {\Pi } _{s}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{s}^{*}\times \mathbf {H} _{s}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8d05cf2ed95277e7bd751fa46642682f4335ffe)
![{\displaystyle \mathbf {\Pi } _{\text{ext}}={\frac {1}{2}}\operatorname {Re} \left[\mathbf {E} _{s}^{*}\times \mathbf {H} _{i}+\mathbf {E} _{i}^{*}\times \mathbf {H} _{s}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e85ec494b9a860683288e7aaae9954f849bf6c7a)













![{\displaystyle \sigma _{\text{abs}}^{\text{(e)}}={\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{e})-{\frac {k^{3}}{6\pi \varepsilon \varepsilon _{0}}}|\alpha ^{e}|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb10384df7b8cd225bce5a949742001a232ea7b2)
![{\displaystyle \sigma _{\text{abs}}^{\text{(m)}}={\frac {1}{4\pi \mu \mu _{0}}}\cdot 4\pi k\left[\Im (\alpha ^{m})-{\frac {k^{3}}{6\pi \mu \mu _{0}}}|\alpha ^{m}|^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2780bc02b1b8e064046963fe09eee7639dc0df1)

![{\displaystyle {\frac {1}{4\pi \varepsilon \varepsilon _{0}}}\Im (\alpha ^{e})+{\frac {1}{4\pi \mu \mu _{0}}}\Im (\alpha ^{m})\geq {\frac {2k^{3}}{3}}\left[{\frac {|\alpha ^{e}|^{2}}{(4\pi \varepsilon \varepsilon _{0})^{2}}}+{\frac {|\alpha ^{m}|^{2}}{(4\pi \mu \mu _{0})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfac79c4c3ae0bea03af629285507e620758a647)


















