Divisor

In mathematics, a divisor of an integer $n$ , also called a factor of $n$ , is an integer which divides $n$ without leaving a remainder.

Terminology

The name "divisor" comes from the arithmetic operation of division: if $a/b=c$ then $a$ is the dividend, $b$ the divisor, and $c$ the quotient.

In general, for non-zero integers $m$ and $n$ , it is said that $m$ divides $n$ , written:

m\mid n,

if there exists an integer $k$ such that $n=km$ . Thus, divisors can be negative as well as positive, although sometimes the term is restricted to positive divisors. (For example, there are six divisors of four, 1, 2, 4, −1, −2, −4, but only the positive ones would usually be mentioned, i.e. 1, 2, and 4.)

1 and −1 divide (are divisors of) every integer, every integer (and its negation) is a divisor of itself, and every integer is a divisor of 0, except by convention 0 itself (see also division by zero). Numbers divisible by 2 are called even and numbers not divisible by 2 are called odd.

1, −1, n and −n are known as the trivial divisors of n. A divisor of n that is not a trivial divisor is known as a non-trivial divisor. A number with at least one non-trivial divisor is known as a composite number, while the units −1 and 1 and prime numbers have no non-trivial divisors.

There are divisibility rules which allow one to recognize certain divisors of a number from the number's digits.

The generalization can be said to be the concept of divisibility in any integral domain.

Examples

7 is a divisor of 42 because $42/7=6$ , so we can say $7\mid 42$ . It can also be said that 42 is divisible by 7, 42 is a multiple of 7, 7 divides 42, or 7 is a factor of 42.
The non-trivial divisors of 6 are 2, −2, 3, −3.
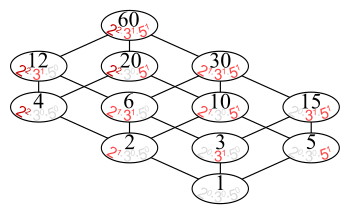
The positive divisors of 42 are 1, 2, 3, 6, 7, 14, 21, 42.
The set of all positive divisors of 60, $A=\{1,2,3,4,5,6,10,12,15,20,30,60\}$ , partially ordered by divisibility, has the Hasse diagram:

Further notions and facts

There are some elementary rules:

If $a\mid b$ and $b\mid c$ , then $a\mid c$ . This is the transitive relation.
If $a\mid b$ and $b\mid a$ , then $a=b$ or $a=-b$ .
If $a\mid b$ and $c\mid b$ , then it is NOT always true that $(a+c)\mid b$ (e.g. $2\mid 6$ and $3\mid 6$ but 5 does not divide 6). However, when $a\mid b$ and $a\mid c$ , then $a\mid (b+c)$ is true, as is $a\mid (b-c)$ .^[1]

The vertical bar used is a Unicode "Divides" character, code point U+2223 and written in TeX as \mid: $\mid$ . Its negated symbol is ∤, or written in TeX as \nmid: $\nmid$ . In an ASCII-only environment, the standard vertical bar "|", which is slightly shorter, is often used.

If $a\mid bc$ , and gcd $(a,b)=1$ , then $a\mid c$ . This is called Euclid's lemma.

If $p$ is a prime number and $p\mid ab$ then $p\mid a$ or $p\mid b$ (or both).

A positive divisor of $n$ which is different from $n$ is called a proper divisor or an aliquot part of $n$ . A number that does not evenly divide $n$ but leaves a remainder is called an aliquant part of $n$ .

An integer $n>1$ whose only proper divisor is 1 is called a prime number. Equivalently, a prime number is a positive integer which has exactly two positive factors: 1 and itself.

Any positive divisor of $n$ is a product of prime divisors of $n$ raised to some power. This is a consequence of the fundamental theorem of arithmetic.

If a number equals the sum of its proper divisors, it is said to be a perfect number. Numbers less than the sum of their proper divisors are said to be abundant, while numbers greater than that sum are said to be deficient.

The total number of positive divisors of $n$ is a multiplicative function $d(n)$ , meaning that when two numbers $m$ and $n$ are relatively prime, then $d(mn)=d(m)\times d(n)$ . For instance, $d(42)=8=2\times 2\times 2=d(2)\times d(3)\times d(7)$ ; the eight divisors of 42 are 1, 2, 3, 6, 7, 14, 21 and 42). However the number of positive divisors is not a totally multiplicative function: if the two numbers $m$ and $n$ share a common divisor, then it might not be true that $d(mn)=d(m)\times d(n)$ . The sum of the positive divisors of $n$ is another multiplicative function $\sigma (n)$ (e.g. $\sigma (42)=96=3\times 4\times 8=\sigma (2)\times \sigma (3)\times \sigma (7)=1+2+3+6+7+14+21+42$ ). Both of these functions are examples of divisor functions.

If the prime factorization of $n$ is given by

n=p_{1}^{\nu _{1}}\,p_{2}^{\nu _{2}}\cdots p_{k}^{\nu _{k}}

then the number of positive divisors of $n$ is

d(n)=(\nu _{1}+1)(\nu _{2}+1)\cdots (\nu _{k}+1),

and each of the divisors has the form

p_{1}^{\mu _{1}}\,p_{2}^{\mu _{2}}\cdots p_{k}^{\mu _{k}}

where $0\leq \mu _{i}\leq \nu _{i}$ for each $1\leq i\leq k.$

It can be shown that for any natural $n$ the inequality $d(n)<2{\sqrt {n}}$ holds.

Also it can be shown ^[2] that

d(1)+d(2)+\cdots +d(n)=n\ln n+(2\gamma -1)n+O({\sqrt {n}}).

One interpretation of this result is that a randomly chosen positive integer n has an expected number of divisors of about $\ln n$ .

In abstract algebra

The relation of divisibility turns the set $N$ of non-negative integers into a partially ordered set, in fact into a complete distributive lattice. The largest element of this lattice is 0 and the smallest is 1. The meet operation ^ is given by the greatest common divisor and the join operation v by the least common multiple. This lattice is isomorphic to the dual of the lattice of subgroups of the infinite cyclic group $Z$ .

Notes

^ $a\mid b,\,a\mid c\Rightarrow b=ja,\,c=ka\Rightarrow b+c=(j+k)a\Rightarrow a\mid (b+c)$ Similarly, $a\mid b,\,a\mid c\Rightarrow b=ja,\,c=ka\Rightarrow b-c=(j-k)a\Rightarrow a\mid (b-c)$
^ Hardy, G. H. (April 17, 1980). An Introduction to the Theory of Numbers. Oxford University Press. p. 264. ISBN 0-19-853171-0. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

References

Richard K. Guy, Unsolved Problems in Number Theory (3rd ed), Springer Verlag, 2004 ISBN 0-387-20860-7; section B.
Øystein Ore, Number Theory and its History, McGraw–Hill, NY, 1944 (and Dover reprints).

[1] $a\mid b,\,a\mid c\Rightarrow b=ja,\,c=ka\Rightarrow b+c=(j+k)a\Rightarrow a\mid (b+c)$ Similarly, $a\mid b,\,a\mid c\Rightarrow b=ja,\,c=ka\Rightarrow b-c=(j-k)a\Rightarrow a\mid (b-c)$

[2] Hardy, G. H. (April 17, 1980). An Introduction to the Theory of Numbers. Oxford University Press. p. 264. ISBN 0-19-853171-0. {{cite book}}: Unknown parameter |coauthors= ignored (|author= suggested) (help)

[1]

[2]

v t e Divisibility-based sets of integers
Overview	Integer factorization Divisor Unitary divisor Divisor function Prime factor Fundamental theorem of arithmetic
Factorization forms	Prime Composite Semiprime Pronic Sphenic Square-free Powerful Perfect power Achilles Smooth Regular Rough Unusual
Constrained divisor sums	Perfect Almost perfect Quasiperfect Multiply perfect Hemiperfect Hyperperfect Superperfect Unitary perfect Semiperfect Practical Erdős–Nicolas
With many divisors	Abundant Primitive abundant Highly abundant Superabundant Colossally abundant Highly composite Superior highly composite Weird
Aliquot sequence-related	Untouchable Amicable (Triple) Sociable Betrothed
Base-dependent	Equidigital Extravagant Frugal Harshad Polydivisible Smith
Other sets	Arithmetic Deficient Friendly Solitary Sublime Harmonic divisor Descartes Refactorable Superperfect