Interior (topology)

In mathematics, specifically in topology, the interior of a subset S of a topological space X is the union of all subsets of S that are open in X. A point that is in the interior of S is an interior point of S.
The interior of S is the complement of the closure of the complement of S. In this sense interior and closure are dual notions.
The exterior of a set S is the complement of the closure of S; it consists of the points that are in neither the set nor its boundary. The interior, boundary, and exterior of a subset together partition the whole space into three blocks (or fewer when one or more of these is empty).
The interior and exterior of a closed curve are a slightly different concept; see the Jordan curve theorem.
Definitions[edit]
Interior point[edit]
If is a subset of a Euclidean space, then is an interior point of if there exists an open ball centered at which is completely contained in (This is illustrated in the introductory section to this article.)
This definition generalizes to any subset of a metric space with metric : is an interior point of if there exists a real number such that is in whenever the distance
This definition generalizes to topological spaces by replacing "open ball" with "open set". If is a subset of a topological space then is an interior point of in if is contained in an open subset of that is completely contained in (Equivalently, is an interior point of if is a neighbourhood of )
Interior of a set[edit]
The interior of a subset of a topological space denoted by or or can be defined in any of the following equivalent ways:
- is the largest open subset of contained in
- is the union of all open sets of contained in
- is the set of all interior points of
If the space is understood from context then the shorter notation is usually preferred to
Examples[edit]
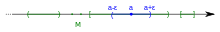
- In any space, the interior of the empty set is the empty set.
- In any space if then
- If is the real line (with the standard topology), then whereas the interior of the set of rational numbers is empty:
- If is the complex plane then
- In any Euclidean space, the interior of any finite set is the empty set.
On the set of real numbers, one can put other topologies rather than the standard one:
- If is the real numbers with the lower limit topology, then
- If one considers on the topology in which every set is open, then
- If one considers on the topology in which the only open sets are the empty set and itself, then is the empty set.
These examples show that the interior of a set depends upon the topology of the underlying space. The last two examples are special cases of the following.
- In any discrete space, since every set is open, every set is equal to its interior.
- In any indiscrete space since the only open sets are the empty set and itself, and for every proper subset of is the empty set.
Properties[edit]
Let be a topological space and let and be subsets of
- is open in
- If is open in then if and only if
- is an open subset of when is given the subspace topology.
- is an open subset of if and only if
- Intensive:
- Idempotence:
- Preserves/distributes over binary intersection:
- However, the interior operator does not distribute over unions since only is guaranteed in general and equality might not hold.[note 1] For example, if and then is a proper subset of
- Monotone/nondecreasing with respect to : If then
Other properties include:
- If is closed in and then
Relationship with closure
The above statements will remain true if all instances of the symbols/words
- "interior", "int", "open", "subset", and "largest"
are respectively replaced by
- "closure", "cl", "closed", "superset", and "smallest"
and the following symbols are swapped:
- "" swapped with ""
- "" swapped with ""
For more details on this matter, see interior operator below or the article Kuratowski closure axioms.
Interior operator[edit]
The interior operator is dual to the closure operator, which is denoted by or by an overline —, in the sense that
In general, the interior operator does not commute with unions. However, in a complete metric space the following result does hold:
Theorem[1] (C. Ursescu) — Let be a sequence of subsets of a complete metric space
- If each is closed in then
- If each is open in then
The result above implies that every complete metric space is a Baire space.
Exterior of a set[edit]
The exterior of a subset of a topological space denoted by or simply is the largest open set disjoint from namely, it is the union of all open sets in that are disjoint from The exterior is the interior of the complement, which is the same as the complement of the closure;[2] in formulas,
Similarly, the interior is the exterior of the complement:
The interior, boundary, and exterior of a set together partition the whole space into three blocks (or fewer when one or more of these is empty):
Some of the properties of the exterior operator are unlike those of the interior operator:
- The exterior operator reverses inclusions; if then
- The exterior operator is not idempotent. It does have the property that
Interior-disjoint shapes[edit]

Two shapes and are called interior-disjoint if the intersection of their interiors is empty. Interior-disjoint shapes may or may not intersect in their boundary.
See also[edit]
- Algebraic interior – Generalization of topological interior
- DE-9IM – topological model and a standard used to describe the spatial relations of two geometries
- Interior algebra – Algebraic structure
- Jordan curve theorem – A closed curve divides the plane into two regions
- Quasi-relative interior – Generalization of algebraic interior
- Relative interior – Generalization of topological interior
References[edit]
- ^ Zalinescu, C (2002). Convex analysis in general vector spaces. River Edge, N.J. London: World Scientific. p. 33. ISBN 981-238-067-1. OCLC 285163112.
- ^ Bourbaki 1989, p. 24.
- ^ Bourbaki 1989, p. 25.
- ^ The analogous identity for the closure operator is These identities may be remembered with the following mnemonic. Just as the intersection of two open sets is open, so too does the interior operator distribute over intersections explicitly: And similarly, just as the union of two closed sets is closed, so too does the closure operator distribute over unions explicitly:
Bibliography[edit]
- Bourbaki, Nicolas (1989) [1966]. General Topology: Chapters 1–4 [Topologie Générale]. Éléments de mathématique. Berlin New York: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC 18588129.
- Dixmier, Jacques (1984). General Topology. Undergraduate Texts in Mathematics. Translated by Berberian, S. K. New York: Springer-Verlag. ISBN 978-0-387-90972-1. OCLC 10277303.
- Császár, Ákos (1978). General topology. Translated by Császár, Klára. Bristol England: Adam Hilger Ltd. ISBN 0-85274-275-4. OCLC 4146011.
- Dugundji, James (1966). Topology. Boston: Allyn and Bacon. ISBN 978-0-697-06889-7. OCLC 395340485.
- Joshi, K. D. (1983). Introduction to General Topology. New York: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7. OCLC 9218750.
- Kelley, John L. (1975). General Topology. Graduate Texts in Mathematics. Vol. 27. New York: Springer Science & Business Media. ISBN 978-0-387-90125-1. OCLC 338047.
- Munkres, James R. (2000). Topology (Second ed.). Upper Saddle River, NJ: Prentice Hall, Inc. ISBN 978-0-13-181629-9. OCLC 42683260.
- Schubert, Horst (1968). Topology. London: Macdonald & Co. ISBN 978-0-356-02077-8. OCLC 463753.
- Wilansky, Albert (17 October 2008) [1970]. Topology for Analysis. Mineola, New York: Dover Publications, Inc. ISBN 978-0-486-46903-4. OCLC 227923899.
- Willard, Stephen (2004) [1970]. General Topology. Mineola, N.Y.: Dover Publications. ISBN 978-0-486-43479-7. OCLC 115240.
External links[edit]
- Interior at PlanetMath.





















![{\displaystyle \operatorname {int} ([0,1])=(0,1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eae21bcb101c4c8272c0dea5b702f6d45c4e41f3)




![{\displaystyle \operatorname {int} ([0,1])=[0,1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/462127a25e835a105261d2ab1af21a58fa6a57dc)
![{\displaystyle \operatorname {int} ([0,1])=[0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77c15a0009575dffc2fc463b2ee6906e0415a6c6)
![{\displaystyle \operatorname {int} ([0,1])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36bdb0cc1182aa30ceb94ec21112619da5096546)









![{\displaystyle X=\mathbb {R} ,S=(-\infty ,0],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/469f60a07978dd867601ddc85db58d60a224b654)


































