Feature selection
This article includes a list of general references, but it lacks sufficient corresponding inline citations. (July 2010) |
In machine learning, feature selection is the process of selecting a subset of relevant features (variables, predictors) for use in model construction. Feature selection techniques are used for several reasons:
- simplification of models to make them easier to interpret,[1]
- shorter training times,[2]
- to avoid the curse of dimensionality,[3]
- improve the compatibility of the data with a certain learning model class,[4]
- to encode inherent symmetries present in the input space.[5][6][7][8]
The central premise when using feature selection is that data sometimes contains features that are redundant or irrelevant, and can thus be removed without incurring much loss of information.[9] Redundancy and irrelevance are two distinct notions, since one relevant feature may be redundant in the presence of another relevant feature with which it is strongly correlated.[10]
Feature extraction creates new features from functions of the original features, whereas feature selection finds a subset of the features. Feature selection techniques are often used in domains where there are many features and comparatively few samples (data points).
Introduction
[edit]A feature selection algorithm can be seen as the combination of a search technique for proposing new feature subsets, along with an evaluation measure which scores the different feature subsets. The simplest algorithm is to test each possible subset of features finding the one which minimizes the error rate. This is an exhaustive search of the space, and is computationally intractable for all but the smallest of feature sets. The choice of evaluation metric heavily influences the algorithm, and it is these evaluation metrics which distinguish between the three main categories of feature selection algorithms: wrappers, filters and embedded methods.[10]
- Wrapper methods use a predictive model to score feature subsets. Each new subset is used to train a model, which is tested on a hold-out set. Counting the number of mistakes made on that hold-out set (the error rate of the model) gives the score for that subset. As wrapper methods train a new model for each subset, they are very computationally intensive, but usually provide the best performing feature set for that particular type of model or typical problem.
- Filter methods use a proxy measure instead of the error rate to score a feature subset. This measure is chosen to be fast to compute, while still capturing the usefulness of the feature set. Common measures include the mutual information,[10] the pointwise mutual information,[11] Pearson product-moment correlation coefficient, Relief-based algorithms,[12] and inter/intra class distance or the scores of significance tests for each class/feature combinations.[11][13] Filters are usually less computationally intensive than wrappers, but they produce a feature set which is not tuned to a specific type of predictive model.[14] This lack of tuning means a feature set from a filter is more general than the set from a wrapper, usually giving lower prediction performance than a wrapper. However the feature set doesn't contain the assumptions of a prediction model, and so is more useful for exposing the relationships between the features. Many filters provide a feature ranking rather than an explicit best feature subset, and the cut off point in the ranking is chosen via cross-validation. Filter methods have also been used as a preprocessing step for wrapper methods, allowing a wrapper to be used on larger problems. One other popular approach is the Recursive Feature Elimination algorithm,[15] commonly used with Support Vector Machines to repeatedly construct a model and remove features with low weights.
- Embedded methods are a catch-all group of techniques which perform feature selection as part of the model construction process. The exemplar of this approach is the LASSO method for constructing a linear model, which penalizes the regression coefficients with an L1 penalty, shrinking many of them to zero. Any features which have non-zero regression coefficients are 'selected' by the LASSO algorithm. Improvements to the LASSO include Bolasso which bootstraps samples;[16] Elastic net regularization, which combines the L1 penalty of LASSO with the L2 penalty of ridge regression; and FeaLect which scores all the features based on combinatorial analysis of regression coefficients.[17] AEFS further extends LASSO to nonlinear scenario with autoencoders.[18] These approaches tend to be between filters and wrappers in terms of computational complexity.
In traditional regression analysis, the most popular form of feature selection is stepwise regression, which is a wrapper technique. It is a greedy algorithm that adds the best feature (or deletes the worst feature) at each round. The main control issue is deciding when to stop the algorithm. In machine learning, this is typically done by cross-validation. In statistics, some criteria are optimized. This leads to the inherent problem of nesting. More robust methods have been explored, such as branch and bound and piecewise linear network.
Subset selection
[edit]Subset selection evaluates a subset of features as a group for suitability. Subset selection algorithms can be broken up into wrappers, filters, and embedded methods. Wrappers use a search algorithm to search through the space of possible features and evaluate each subset by running a model on the subset. Wrappers can be computationally expensive and have a risk of over fitting to the model. Filters are similar to wrappers in the search approach, but instead of evaluating against a model, a simpler filter is evaluated. Embedded techniques are embedded in, and specific to, a model.
Many popular search approaches use greedy hill climbing, which iteratively evaluates a candidate subset of features, then modifies the subset and evaluates if the new subset is an improvement over the old. Evaluation of the subsets requires a scoring metric that grades a subset of features. Exhaustive search is generally impractical, so at some implementor (or operator) defined stopping point, the subset of features with the highest score discovered up to that point is selected as the satisfactory feature subset. The stopping criterion varies by algorithm; possible criteria include: a subset score exceeds a threshold, a program's maximum allowed run time has been surpassed, etc.
Alternative search-based techniques are based on targeted projection pursuit which finds low-dimensional projections of the data that score highly: the features that have the largest projections in the lower-dimensional space are then selected.
Search approaches include:
- Exhaustive[19]
- Best first
- Simulated annealing
- Genetic algorithm[20]
- Greedy forward selection[21][22][23]
- Greedy backward elimination
- Particle swarm optimization[24]
- Targeted projection pursuit
- Scatter search[25][26]
- Variable neighborhood search[27][28]
Two popular filter metrics for classification problems are correlation and mutual information, although neither are true metrics or 'distance measures' in the mathematical sense, since they fail to obey the triangle inequality and thus do not compute any actual 'distance' – they should rather be regarded as 'scores'. These scores are computed between a candidate feature (or set of features) and the desired output category. There are, however, true metrics that are a simple function of the mutual information;[29] see here.
Other available filter metrics include:
- Class separability
- Error probability
- Inter-class distance
- Probabilistic distance
- Entropy
- Consistency-based feature selection
- Correlation-based feature selection
Optimality criteria
[edit]The choice of optimality criteria is difficult as there are multiple objectives in a feature selection task. Many common criteria incorporate a measure of accuracy, penalised by the number of features selected. Examples include Akaike information criterion (AIC) and Mallows's Cp, which have a penalty of 2 for each added feature. AIC is based on information theory, and is effectively derived via the maximum entropy principle.[30][31]
Other criteria are Bayesian information criterion (BIC), which uses a penalty of for each added feature, minimum description length (MDL) which asymptotically uses , Bonferroni / RIC which use , maximum dependency feature selection, and a variety of new criteria that are motivated by false discovery rate (FDR), which use something close to . A maximum entropy rate criterion may also be used to select the most relevant subset of features.[32]
Structure learning
[edit]Filter feature selection is a specific case of a more general paradigm called structure learning. Feature selection finds the relevant feature set for a specific target variable whereas structure learning finds the relationships between all the variables, usually by expressing these relationships as a graph. The most common structure learning algorithms assume the data is generated by a Bayesian Network, and so the structure is a directed graphical model. The optimal solution to the filter feature selection problem is the Markov blanket of the target node, and in a Bayesian Network, there is a unique Markov Blanket for each node.[33]
Information Theory Based Feature Selection Mechanisms
[edit]There are different Feature Selection mechanisms around that utilize mutual information for scoring the different features. They usually use all the same algorithm:
- Calculate the mutual information as score for between all features () and the target class (c)
- Select the feature with the largest score (e.g. ) and add it to the set of selected features (S)
- Calculate the score which might be derived from the mutual information
- Select the feature with the largest score and add it to the set of select features (e.g. )
- Repeat 3. and 4. until a certain number of features is selected (e.g. )
The simplest approach uses the mutual information as the "derived" score.[34]
However, there are different approaches, that try to reduce the redundancy between features.
Minimum-redundancy-maximum-relevance (mRMR) feature selection
[edit]Peng et al.[35] proposed a feature selection method that can use either mutual information, correlation, or distance/similarity scores to select features. The aim is to penalise a feature's relevancy by its redundancy in the presence of the other selected features. The relevance of a feature set S for the class c is defined by the average value of all mutual information values between the individual feature fi and the class c as follows:
- .
The redundancy of all features in the set S is the average value of all mutual information values between the feature fi and the feature fj:
The mRMR criterion is a combination of two measures given above and is defined as follows:
Suppose that there are n full-set features. Let xi be the set membership indicator function for feature fi, so that xi=1 indicates presence and xi=0 indicates absence of the feature fi in the globally optimal feature set. Let and . The above may then be written as an optimization problem:
The mRMR algorithm is an approximation of the theoretically optimal maximum-dependency feature selection algorithm that maximizes the mutual information between the joint distribution of the selected features and the classification variable. As mRMR approximates the combinatorial estimation problem with a series of much smaller problems, each of which only involves two variables, it thus uses pairwise joint probabilities which are more robust. In certain situations the algorithm may underestimate the usefulness of features as it has no way to measure interactions between features which can increase relevancy. This can lead to poor performance[34] when the features are individually useless, but are useful when combined (a pathological case is found when the class is a parity function of the features). Overall the algorithm is more efficient (in terms of the amount of data required) than the theoretically optimal max-dependency selection, yet produces a feature set with little pairwise redundancy.
mRMR is an instance of a large class of filter methods which trade off between relevancy and redundancy in different ways.[34][36]
Quadratic programming feature selection
[edit]mRMR is a typical example of an incremental greedy strategy for feature selection: once a feature has been selected, it cannot be deselected at a later stage. While mRMR could be optimized using floating search to reduce some features, it might also be reformulated as a global quadratic programming optimization problem as follows:[37]
where is the vector of feature relevancy assuming there are n features in total, is the matrix of feature pairwise redundancy, and represents relative feature weights. QPFS is solved via quadratic programming. It is recently shown that QFPS is biased towards features with smaller entropy,[38] due to its placement of the feature self redundancy term on the diagonal of H.
Conditional mutual information
[edit]Another score derived for the mutual information is based on the conditional relevancy:[38]
where and .
An advantage of SPECCMI is that it can be solved simply via finding the dominant eigenvector of Q, thus is very scalable. SPECCMI also handles second-order feature interaction.
Joint mutual information
[edit]In a study of different scores Brown et al.[34] recommended the joint mutual information[39] as a good score for feature selection. The score tries to find the feature, that adds the most new information to the already selected features, in order to avoid redundancy. The score is formulated as follows:
The score uses the conditional mutual information and the mutual information to estimate the redundancy between the already selected features () and the feature under investigation ().
Hilbert-Schmidt Independence Criterion Lasso based feature selection
[edit]For high-dimensional and small sample data (e.g., dimensionality > 105 and the number of samples < 103), the Hilbert-Schmidt Independence Criterion Lasso (HSIC Lasso) is useful.[40] HSIC Lasso optimization problem is given as
where is a kernel-based independence measure called the (empirical) Hilbert-Schmidt independence criterion (HSIC), denotes the trace, is the regularization parameter, and are input and output centered Gram matrices, and are Gram matrices, and are kernel functions, is the centering matrix, is the m-dimensional identity matrix (m: the number of samples), is the m-dimensional vector with all ones, and is the -norm. HSIC always takes a non-negative value, and is zero if and only if two random variables are statistically independent when a universal reproducing kernel such as the Gaussian kernel is used.
The HSIC Lasso can be written as
where is the Frobenius norm. The optimization problem is a Lasso problem, and thus it can be efficiently solved with a state-of-the-art Lasso solver such as the dual augmented Lagrangian method.
Correlation feature selection
[edit]The correlation feature selection (CFS) measure evaluates subsets of features on the basis of the following hypothesis: "Good feature subsets contain features highly correlated with the classification, yet uncorrelated to each other".[41][42] The following equation gives the merit of a feature subset S consisting of k features:
Here, is the average value of all feature-classification correlations, and is the average value of all feature-feature correlations. The CFS criterion is defined as follows:
The and variables are referred to as correlations, but are not necessarily Pearson's correlation coefficient or Spearman's ρ. Hall's dissertation uses neither of these, but uses three different measures of relatedness, minimum description length (MDL), symmetrical uncertainty, and relief.
Let xi be the set membership indicator function for feature fi; then the above can be rewritten as an optimization problem:
The combinatorial problems above are, in fact, mixed 0–1 linear programming problems that can be solved by using branch-and-bound algorithms.[43]
Regularized trees
[edit]The features from a decision tree or a tree ensemble are shown to be redundant. A recent method called regularized tree[44] can be used for feature subset selection. Regularized trees penalize using a variable similar to the variables selected at previous tree nodes for splitting the current node. Regularized trees only need build one tree model (or one tree ensemble model) and thus are computationally efficient.
Regularized trees naturally handle numerical and categorical features, interactions and nonlinearities. They are invariant to attribute scales (units) and insensitive to outliers, and thus, require little data preprocessing such as normalization. Regularized random forest (RRF)[45] is one type of regularized trees. The guided RRF is an enhanced RRF which is guided by the importance scores from an ordinary random forest.
Overview on metaheuristics methods
[edit]A metaheuristic is a general description of an algorithm dedicated to solve difficult (typically NP-hard problem) optimization problems for which there is no classical solving methods. Generally, a metaheuristic is a stochastic algorithm tending to reach a global optimum. There are many metaheuristics, from a simple local search to a complex global search algorithm.
Main principles
[edit]The feature selection methods are typically presented in three classes based on how they combine the selection algorithm and the model building.
Filter method
[edit]
Filter type methods select variables regardless of the model. They are based only on general features like the correlation with the variable to predict. Filter methods suppress the least interesting variables. The other variables will be part of a classification or a regression model used to classify or to predict data. These methods are particularly effective in computation time and robust to overfitting.[46]
Filter methods tend to select redundant variables when they do not consider the relationships between variables. However, more elaborate features try to minimize this problem by removing variables highly correlated to each other, such as the Fast Correlation Based Filter (FCBF) algorithm.[47]
Wrapper method
[edit]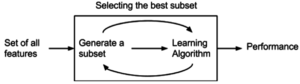
Wrapper methods evaluate subsets of variables which allows, unlike filter approaches, to detect the possible interactions amongst variables.[48] The two main disadvantages of these methods are:
- The increasing overfitting risk when the number of observations is insufficient.
- The significant computation time when the number of variables is large.
Embedded method
[edit]
Embedded methods have been recently proposed that try to combine the advantages of both previous methods. A learning algorithm takes advantage of its own variable selection process and performs feature selection and classification simultaneously, such as the FRMT algorithm.[49]
Application of feature selection metaheuristics
[edit]This is a survey of the application of feature selection metaheuristics lately used in the literature. This survey was realized by J. Hammon in her 2013 thesis.[46]
| Application | Algorithm | Approach | Classifier | Evaluation Function | Reference |
|---|---|---|---|---|---|
| SNPs | Feature Selection using Feature Similarity | Filter | r2 | Phuong 2005[48] | |
| SNPs | Genetic algorithm | Wrapper | Decision Tree | Classification accuracy (10-fold) | Shah 2004[50] |
| SNPs | Hill climbing | Filter + Wrapper | Naive Bayesian | Predicted residual sum of squares | Long 2007[51] |
| SNPs | Simulated annealing | Naive bayesian | Classification accuracy (5-fold) | Ustunkar 2011[52] | |
| Segments parole | Ant colony | Wrapper | Artificial Neural Network | MSE | Al-ani 2005 [citation needed] |
| Marketing | Simulated annealing | Wrapper | Regression | AIC, r2 | Meiri 2006[53] |
| Economics | Simulated annealing, genetic algorithm | Wrapper | Regression | BIC | Kapetanios 2007[54] |
| Spectral Mass | Genetic algorithm | Wrapper | Multiple Linear Regression, Partial Least Squares | root-mean-square error of prediction | Broadhurst et al. 1997[55] |
| Spam | Binary PSO + Mutation | Wrapper | Decision tree | weighted cost | Zhang 2014[24] |
| Microarray | Tabu search + PSO | Wrapper | Support Vector Machine, K Nearest Neighbors | Euclidean Distance | Chuang 2009[56] |
| Microarray | PSO + Genetic algorithm | Wrapper | Support Vector Machine | Classification accuracy (10-fold) | Alba 2007[57] |
| Microarray | Genetic algorithm + Iterated Local Search | Embedded | Support Vector Machine | Classification accuracy (10-fold) | Duval 2009[58] |
| Microarray | Iterated local search | Wrapper | Regression | Posterior Probability | Hans 2007[59] |
| Microarray | Genetic algorithm | Wrapper | K Nearest Neighbors | Classification accuracy (Leave-one-out cross-validation) | Jirapech-Umpai 2005[60] |
| Microarray | Hybrid genetic algorithm | Wrapper | K Nearest Neighbors | Classification accuracy (Leave-one-out cross-validation) | Oh 2004[61] |
| Microarray | Genetic algorithm | Wrapper | Support Vector Machine | Sensitivity and specificity | Xuan 2011[62] |
| Microarray | Genetic algorithm | Wrapper | All paired Support Vector Machine | Classification accuracy (Leave-one-out cross-validation) | Peng 2003[63] |
| Microarray | Genetic algorithm | Embedded | Support Vector Machine | Classification accuracy (10-fold) | Hernandez 2007[64] |
| Microarray | Genetic algorithm | Hybrid | Support Vector Machine | Classification accuracy (Leave-one-out cross-validation) | Huerta 2006[65] |
| Microarray | Genetic algorithm | Support Vector Machine | Classification accuracy (10-fold) | Muni 2006[66] | |
| Microarray | Genetic algorithm | Wrapper | Support Vector Machine | EH-DIALL, CLUMP | Jourdan 2005[67] |
| Alzheimer's disease | Welch's t-test | Filter | Support vector machine | Classification accuracy (10-fold) | Zhang 2015[68] |
| Computer vision | Infinite Feature Selection | Filter | Independent | Average Precision, ROC AUC | Roffo 2015[69] |
| Microarrays | Eigenvector Centrality FS | Filter | Independent | Average Precision, Accuracy, ROC AUC | Roffo & Melzi 2016[70] |
| XML | Symmetrical Tau (ST) | Filter | Structural Associative Classification | Accuracy, Coverage | Shaharanee & Hadzic 2014 |
Feature selection embedded in learning algorithms
[edit]Some learning algorithms perform feature selection as part of their overall operation. These include:
- -regularization techniques, such as sparse regression, LASSO, and -SVM
- Regularized trees,[44] e.g. regularized random forest implemented in the RRF package[45]
- Decision tree[71]
- Memetic algorithm
- Random multinomial logit (RMNL)
- Auto-encoding networks with a bottleneck-layer
- Submodular feature selection[72][73][74]
- Local learning based feature selection.[75] Compared with traditional methods, it does not involve any heuristic search, can easily handle multi-class problems, and works for both linear and nonlinear problems. It is also supported by a strong theoretical foundation. Numeric experiments showed that the method can achieve a close-to-optimal solution even when data contains >1M irrelevant features.
- Recommender system based on feature selection.[76] The feature selection methods are introduced into recommender system research.
See also
[edit]- Cluster analysis
- Data mining
- Dimensionality reduction
- Feature extraction
- Hyperparameter optimization
- Model selection
- Relief (feature selection)
References
[edit]- ^ Gareth James; Daniela Witten; Trevor Hastie; Robert Tibshirani (2013). An Introduction to Statistical Learning. Springer. p. 204.
- ^ Brank, Janez; Mladenić, Dunja; Grobelnik, Marko; Liu, Huan; Mladenić, Dunja; Flach, Peter A.; Garriga, Gemma C.; Toivonen, Hannu; Toivonen, Hannu (2011), "Feature Selection", in Sammut, Claude; Webb, Geoffrey I. (eds.), Encyclopedia of Machine Learning, Boston, MA: Springer US, pp. 402–406, doi:10.1007/978-0-387-30164-8_306, ISBN 978-0-387-30768-8, retrieved 2021-07-13
- ^ Kramer, Mark A. (1991). "Nonlinear principal component analysis using autoassociative neural networks". AIChE Journal. 37 (2): 233–243. Bibcode:1991AIChE..37..233K. doi:10.1002/aic.690370209. ISSN 1547-5905.
- ^ Kratsios, Anastasis; Hyndman, Cody (2021). "NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation". Journal of Machine Learning Research. 22 (92): 1–51. ISSN 1533-7928.
- ^ Persello, Claudio; Bruzzone, Lorenzo (July 2014). "Relevant and invariant feature selection of hyperspectral images for domain generalization". 2014 IEEE Geoscience and Remote Sensing Symposium (PDF). IEEE. pp. 3562–3565. doi:10.1109/igarss.2014.6947252. ISBN 978-1-4799-5775-0. S2CID 8368258.
- ^ Hinkle, Jacob; Muralidharan, Prasanna; Fletcher, P. Thomas; Joshi, Sarang (2012). "Polynomial Regression on Riemannian Manifolds". In Fitzgibbon, Andrew; Lazebnik, Svetlana; Perona, Pietro; Sato, Yoichi; Schmid, Cordelia (eds.). Computer Vision – ECCV 2012. Lecture Notes in Computer Science. Vol. 7574. Berlin, Heidelberg: Springer. pp. 1–14. arXiv:1201.2395. doi:10.1007/978-3-642-33712-3_1. ISBN 978-3-642-33712-3. S2CID 8849753.
- ^ Yarotsky, Dmitry (2021-04-30). "Universal Approximations of Invariant Maps by Neural Networks". Constructive Approximation. 55: 407–474. arXiv:1804.10306. doi:10.1007/s00365-021-09546-1. ISSN 1432-0940. S2CID 13745401.
- ^ Hauberg, Søren; Lauze, François; Pedersen, Kim Steenstrup (2013-05-01). "Unscented Kalman Filtering on Riemannian Manifolds". Journal of Mathematical Imaging and Vision. 46 (1): 103–120. Bibcode:2013JMIV...46..103H. doi:10.1007/s10851-012-0372-9. ISSN 1573-7683. S2CID 8501814.
- ^ Kratsios, Anastasis; Hyndman, Cody (June 8, 2021). "NEU: A Meta-Algorithm for Universal UAP-Invariant Feature Representation". Journal of Machine Learning Research. 22: 10312. Bibcode:2015NatSR...510312B. doi:10.1038/srep10312. PMC 4437376. PMID 25988841.
- ^ a b c Guyon, Isabelle; Elisseeff, André (2003). "An Introduction to Variable and Feature Selection". JMLR. 3.
- ^ a b Yang, Yiming; Pedersen, Jan O. (1997). A comparative study on feature selection in text categorization (PDF). ICML.
- ^ Urbanowicz, Ryan J.; Meeker, Melissa; LaCava, William; Olson, Randal S.; Moore, Jason H. (2018). "Relief-Based Feature Selection: Introduction and Review". Journal of Biomedical Informatics. 85: 189–203. arXiv:1711.08421. doi:10.1016/j.jbi.2018.07.014. PMC 6299836. PMID 30031057.
- ^ Forman, George (2003). "An extensive empirical study of feature selection metrics for text classification" (PDF). Journal of Machine Learning Research. 3: 1289–1305.
- ^ Yishi Zhang; Shujuan Li; Teng Wang; Zigang Zhang (2013). "Divergence-based feature selection for separate classes". Neurocomputing. 101 (4): 32–42. doi:10.1016/j.neucom.2012.06.036.
- ^ Guyon I.; Weston J.; Barnhill S.; Vapnik V. (2002). "Gene selection for cancer classification using support vector machines". Machine Learning. 46 (1–3): 389–422. doi:10.1023/A:1012487302797.
- ^ Bach, Francis R (2008). "Bolasso". Proceedings of the 25th international conference on Machine learning - ICML '08. pp. 33–40. doi:10.1145/1390156.1390161. ISBN 9781605582054. S2CID 609778.
- ^ Zare, Habil (2013). "Scoring relevancy of features based on combinatorial analysis of Lasso with application to lymphoma diagnosis". BMC Genomics. 14 (Suppl 1): S14. doi:10.1186/1471-2164-14-S1-S14. PMC 3549810. PMID 23369194.
- ^ Kai Han; Yunhe Wang; Chao Zhang; Chao Li; Chao Xu (2018). Autoencoder inspired unsupervised feature selection. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).
- ^ Hazimeh, Hussein; Mazumder, Rahul; Saab, Ali (2020). "Sparse Regression at Scale: Branch-and-Bound rooted in First-Order Optimization". arXiv:2004.06152 [stat.CO].
- ^ Soufan, Othman; Kleftogiannis, Dimitrios; Kalnis, Panos; Bajic, Vladimir B. (2015-02-26). "DWFS: A Wrapper Feature Selection Tool Based on a Parallel Genetic Algorithm". PLOS ONE. 10 (2): e0117988. Bibcode:2015PLoSO..1017988S. doi:10.1371/journal.pone.0117988. ISSN 1932-6203. PMC 4342225. PMID 25719748.
- ^ Figueroa, Alejandro (2015). "Exploring effective features for recognizing the user intent behind web queries". Computers in Industry. 68: 162–169. doi:10.1016/j.compind.2015.01.005.
- ^ Figueroa, Alejandro; Guenter Neumann (2013). Learning to Rank Effective Paraphrases from Query Logs for Community Question Answering. AAAI.
- ^ Figueroa, Alejandro; Guenter Neumann (2014). "Category-specific models for ranking effective paraphrases in community Question Answering". Expert Systems with Applications. 41 (10): 4730–4742. doi:10.1016/j.eswa.2014.02.004. hdl:10533/196878.
- ^ a b Zhang, Y.; Wang, S.; Phillips, P. (2014). "Binary PSO with Mutation Operator for Feature Selection using Decision Tree applied to Spam Detection". Knowledge-Based Systems. 64: 22–31. doi:10.1016/j.knosys.2014.03.015.
- ^ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving feature subset selection problem by a Parallel Scatter Search, European Journal of Operational Research, vol. 169, no. 2, pp. 477–489, 2006.
- ^ García-Torres, Miguel; Gómez-Vela, Francisco; Divina, Federico; Pinto-Roa, Diego P.; Noguera, José Luis Vázquez; Román, Julio C. Mello (2021). "Scatter search for high-dimensional feature selection using feature grouping". Proceedings of the Genetic and Evolutionary Computation Conference Companion. pp. 149–150. doi:10.1145/3449726.3459481. ISBN 9781450383516. S2CID 235770316.
- ^ F.C. Garcia-Lopez, M. Garcia-Torres, B. Melian, J.A. Moreno-Perez, J.M. Moreno-Vega. Solving Feature Subset Selection Problem by a Hybrid Metaheuristic. In First International Workshop on Hybrid Metaheuristics, pp. 59–68, 2004.
- ^ M. Garcia-Torres, F. Gomez-Vela, B. Melian, J.M. Moreno-Vega. High-dimensional feature selection via feature grouping: A Variable Neighborhood Search approach, Information Sciences, vol. 326, pp. 102-118, 2016.
- ^ Kraskov, Alexander; Stögbauer, Harald; Andrzejak, Ralph G; Grassberger, Peter (2003). "Hierarchical Clustering Based on Mutual Information". arXiv:q-bio/0311039. Bibcode:2003q.bio....11039K.
{{cite journal}}: Cite journal requires|journal=(help) - ^ Akaike, H. (1985), "Prediction and entropy", in Atkinson, A. C.; Fienberg, S. E. (eds.), A Celebration of Statistics (PDF), Springer, pp. 1–24, archived (PDF) from the original on August 30, 2019.
- ^ Burnham, K. P.; Anderson, D. R. (2002), Model Selection and Multimodel Inference: A practical information-theoretic approach (2nd ed.), Springer-Verlag, ISBN 9780387953649.
- ^ Einicke, G. A. (2018). "Maximum-Entropy Rate Selection of Features for Classifying Changes in Knee and Ankle Dynamics During Running". IEEE Journal of Biomedical and Health Informatics. 28 (4): 1097–1103. doi:10.1109/JBHI.2017.2711487. hdl:10810/68978. PMID 29969403. S2CID 49555941.
- ^ Aliferis, Constantin (2010). "Local causal and markov blanket induction for causal discovery and feature selection for classification part I: Algorithms and empirical evaluation" (PDF). Journal of Machine Learning Research. 11: 171–234.
- ^ a b c d Brown, Gavin; Pocock, Adam; Zhao, Ming-Jie; Luján, Mikel (2012). "Conditional Likelihood Maximisation: A Unifying Framework for Information Theoretic Feature Selection". Journal of Machine Learning Research. 13: 27–66.[1]
- ^ Peng, H. C.; Long, F.; Ding, C. (2005). "Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy". IEEE Transactions on Pattern Analysis and Machine Intelligence. 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765. doi:10.1109/TPAMI.2005.159. PMID 16119262. S2CID 206764015. Program
- ^ Nguyen, H., Franke, K., Petrovic, S. (2010). "Towards a Generic Feature-Selection Measure for Intrusion Detection", In Proc. International Conference on Pattern Recognition (ICPR), Istanbul, Turkey. [2]
- ^ Rodriguez-Lujan, I.; Huerta, R.; Elkan, C.; Santa Cruz, C. (2010). "Quadratic programming feature selection" (PDF). JMLR. 11: 1491–1516.
- ^ a b Nguyen X. Vinh, Jeffrey Chan, Simone Romano and James Bailey, "Effective Global Approaches for Mutual Information based Feature Selection". Proceedings of the 20th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD'14), August 24–27, New York City, 2014. "[3]"
- ^ Yang, Howard Hua; Moody, John (2000). "Data visualization and feature selection: New algorithms for nongaussian data" (PDF). Advances in Neural Information Processing Systems: 687–693.
- ^ Yamada, M.; Jitkrittum, W.; Sigal, L.; Xing, E. P.; Sugiyama, M. (2014). "High-Dimensional Feature Selection by Feature-Wise Non-Linear Lasso". Neural Computation. 26 (1): 185–207. arXiv:1202.0515. doi:10.1162/NECO_a_00537. PMID 24102126. S2CID 2742785.
- ^ Hall, M. (1999). Correlation-based Feature Selection for Machine Learning (PDF) (PhD thesis). University of Waikato.
- ^ Senliol, Baris; et al. (2008). "Fast Correlation Based Filter (FCBF) with a different search strategy". 2008 23rd International Symposium on Computer and Information Sciences. pp. 1–4. doi:10.1109/ISCIS.2008.4717949. ISBN 978-1-4244-2880-9. S2CID 8398495.
- ^ Nguyen, Hai; Franke, Katrin; Petrovic, Slobodan (December 2009). "Optimizing a class of feature selection measures". Proceedings of the NIPS 2009 Workshop on Discrete Optimization in Machine Learning: Submodularity, Sparsity & Polyhedra (DISCML). Vancouver, Canada.
- ^ a b H. Deng, G. Runger, "Feature Selection via Regularized Trees", Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN), IEEE, 2012
- ^ a b RRF: Regularized Random Forest, R package on CRAN
- ^ a b Hamon, Julie (November 2013). Optimisation combinatoire pour la sélection de variables en régression en grande dimension: Application en génétique animale (Thesis) (in French). Lille University of Science and Technology.
- ^ Yu, Lei; Liu, Huan (August 2003). "Feature selection for high-dimensional data: a fast correlation-based filter solution" (PDF). ICML'03: Proceedings of the Twentieth International Conference on International Conference on Machine Learning: 856–863.
- ^ a b T. M. Phuong, Z. Lin et R. B. Altman. Choosing SNPs using feature selection. Archived 2016-09-13 at the Wayback Machine Proceedings / IEEE Computational Systems Bioinformatics Conference, CSB. IEEE Computational Systems Bioinformatics Conference, pages 301-309, 2005. PMID 16447987.
- ^ Saghapour, E.; Kermani, S.; Sehhati, M. (2017). "A novel feature ranking method for prediction of cancer stages using proteomics data". PLOS ONE. 12 (9): e0184203. Bibcode:2017PLoSO..1284203S. doi:10.1371/journal.pone.0184203. PMC 5608217. PMID 28934234.
- ^ Shah, S. C.; Kusiak, A. (2004). "Data mining and genetic algorithm based gene/SNP selection". Artificial Intelligence in Medicine. 31 (3): 183–196. doi:10.1016/j.artmed.2004.04.002. PMID 15302085.
- ^ Long, N.; Gianola, D.; Weigel, K. A (2011). "Dimension reduction and variable selection for genomic selection: application to predicting milk yield in Holsteins". Journal of Animal Breeding and Genetics. 128 (4): 247–257. doi:10.1111/j.1439-0388.2011.00917.x. PMID 21749471.
- ^ Üstünkar, Gürkan; Özöğür-Akyüz, Süreyya; Weber, Gerhard W.; Friedrich, Christoph M.; Aydın Son, Yeşim (2012). "Selection of representative SNP sets for genome-wide association studies: A metaheuristic approach". Optimization Letters. 6 (6): 1207–1218. doi:10.1007/s11590-011-0419-7. S2CID 8075318.
- ^ Meiri, R.; Zahavi, J. (2006). "Using simulated annealing to optimize the feature selection problem in marketing applications". European Journal of Operational Research. 171 (3): 842–858. doi:10.1016/j.ejor.2004.09.010.
- ^ Kapetanios, G. (2007). "Variable Selection in Regression Models using Nonstandard Optimisation of Information Criteria". Computational Statistics & Data Analysis. 52 (1): 4–15. doi:10.1016/j.csda.2007.04.006.
- ^ Broadhurst, D.; Goodacre, R.; Jones, A.; Rowland, J. J.; Kell, D. B. (1997). "Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression, with applications to pyrolysis mass spectrometry". Analytica Chimica Acta. 348 (1–3): 71–86. Bibcode:1997AcAC..348...71B. doi:10.1016/S0003-2670(97)00065-2.
- ^ Chuang, L.-Y.; Yang, C.-H. (2009). "Tabu search and binary particle swarm optimization for feature selection using microarray data". Journal of Computational Biology. 16 (12): 1689–1703. doi:10.1089/cmb.2007.0211. PMID 20047491.
- ^ E. Alba, J. Garia-Nieto, L. Jourdan et E.-G. Talbi. Gene Selection in Cancer Classification using PSO-SVM and GA-SVM Hybrid Algorithms. Archived 2016-08-18 at the Wayback Machine Congress on Evolutionary Computation, Singapore: Singapore (2007), 2007
- ^ B. Duval, J.-K. Hao et J. C. Hernandez Hernandez. A memetic algorithm for gene selection and molecular classification of an cancer. In Proceedings of the 11th Annual conference on Genetic and evolutionary computation, GECCO '09, pages 201-208, New York, NY, USA, 2009. ACM.
- ^ C. Hans, A. Dobra et M. West. Shotgun stochastic search for 'large p' regression. Journal of the American Statistical Association, 2007.
- ^ Aitken, S. (2005). "Feature selection and classification for microarray data analysis: Evolutionary methods for identifying predictive genes". BMC Bioinformatics. 6 (1): 148. doi:10.1186/1471-2105-6-148. PMC 1181625. PMID 15958165.
- ^ Oh, I. S.; Moon, B. R. (2004). "Hybrid genetic algorithms for feature selection". IEEE Transactions on Pattern Analysis and Machine Intelligence. 26 (11): 1424–1437. CiteSeerX 10.1.1.467.4179. doi:10.1109/tpami.2004.105. PMID 15521491.
- ^ Xuan, P.; Guo, M. Z.; Wang, J.; Liu, X. Y.; Liu, Y. (2011). "Genetic algorithm-based efficient feature selection for classification of pre-miRNAs". Genetics and Molecular Research. 10 (2): 588–603. doi:10.4238/vol10-2gmr969. PMID 21491369.
- ^ Peng, S. (2003). "Molecular classification of cancer types from microarray data using the combination of genetic algorithms and support vector machines". FEBS Letters. 555 (2): 358–362. Bibcode:2003FEBSL.555..358P. doi:10.1016/s0014-5793(03)01275-4. PMID 14644442.
- ^ Hernandez, J. C. H.; Duval, B.; Hao, J.-K. (2007). "A Genetic Embedded Approach for Gene Selection and Classification of Microarray Data". Evolutionary Computation, Machine Learning and Data Mining in Bioinformatics. EvoBIO 2007. Lecture Notes in Computer Science. Vol. 4447. Berlin: Springer Verlag. pp. 90–101. doi:10.1007/978-3-540-71783-6_9. ISBN 978-3-540-71782-9.
- ^ Huerta, E. B.; Duval, B.; Hao, J.-K. (2006). "A Hybrid GA/SVM Approach for Gene Selection and Classification of Microarray Data". Applications of Evolutionary Computing. EvoWorkshops 2006. Lecture Notes in Computer Science. Vol. 3907. pp. 34–44. doi:10.1007/11732242_4. ISBN 978-3-540-33237-4.
- ^ Muni, D. P.; Pal, N. R.; Das, J. (2006). "Genetic programming for simultaneous feature selection and classifier design". IEEE Transactions on Systems, Man, and Cybernetics - Part B: Cybernetics. 36 (1): 106–117. doi:10.1109/TSMCB.2005.854499. PMID 16468570. S2CID 2073035.
- ^ Jourdan, L.; Dhaenens, C.; Talbi, E.-G. (2005). "Linkage disequilibrium study with a parallel adaptive GA". International Journal of Foundations of Computer Science. 16 (2): 241–260. doi:10.1142/S0129054105002978.
- ^ Zhang, Y.; Dong, Z.; Phillips, P.; Wang, S. (2015). "Detection of subjects and brain regions related to Alzheimer's disease using 3D MRI scans based on eigenbrain and machine learning". Frontiers in Computational Neuroscience. 9: 66. doi:10.3389/fncom.2015.00066. PMC 4451357. PMID 26082713.
- ^ Roffo, G.; Melzi, S.; Cristani, M. (2015-12-01). "Infinite Feature Selection". 2015 IEEE International Conference on Computer Vision (ICCV). pp. 4202–4210. doi:10.1109/ICCV.2015.478. ISBN 978-1-4673-8391-2. S2CID 3223980.
- ^ Roffo, Giorgio; Melzi, Simone (September 2016). "Features Selection via Eigenvector Centrality" (PDF). NFmcp2016. Retrieved 12 November 2016.
- ^ R. Kohavi and G. John, "Wrappers for feature subset selection", Artificial intelligence 97.1-2 (1997): 273-324
- ^ Das, Abhimanyu; Kempe, David (2011). "Submodular meets Spectral: Greedy Algorithms for Subset Selection, Sparse Approximation and Dictionary Selection". arXiv:1102.3975 [stat.ML].
- ^ Liu et al., Submodular feature selection for high-dimensional acoustic score spaces Archived 2015-10-17 at the Wayback Machine
- ^ Zheng et al., Submodular Attribute Selection for Action Recognition in Video Archived 2015-11-18 at the Wayback Machine
- ^ Sun, Y.; Todorovic, S.; Goodison, S. (2010). "Local-Learning-Based Feature Selection for High-Dimensional Data Analysis". IEEE Transactions on Pattern Analysis and Machine Intelligence. 32 (9): 1610–1626. doi:10.1109/tpami.2009.190. PMC 3445441. PMID 20634556.
- ^ D.H. Wang, Y.C. Liang, D.Xu, X.Y. Feng, R.C. Guan(2018), "A content-based recommender system for computer science publications", Knowledge-Based Systems, 157: 1-9
Further reading
[edit]- Guyon, Isabelle; Elisseeff, Andre (2003). "An Introduction to Variable and Feature Selection". Journal of Machine Learning Research. 3: 1157–1182.
- Harrell, F. (2001). Regression Modeling Strategies. Springer. ISBN 0-387-95232-2.
- Liu, Huan; Motoda, Hiroshi (1998). Feature Selection for Knowledge Discovery and Data Mining. Springer. ISBN 0-7923-8198-X.
- Liu, Huan; Yu, Lei (2005). "Toward Integrating Feature Selection Algorithms for Classification and Clustering". IEEE Transactions on Knowledge and Data Engineering. 17 (4): 491–502. doi:10.1109/TKDE.2005.66. S2CID 1607600.
External links
[edit]- Feature Selection Package, Arizona State University (Matlab Code)
- NIPS challenge 2003 (see also NIPS)
- Naive Bayes implementation with feature selection in Visual Basic Archived 2009-02-14 at the Wayback Machine (includes executable and source code)
- Minimum-redundancy-maximum-relevance (mRMR) feature selection program
- FEAST (Open source Feature Selection algorithms in C and MATLAB)










![{\displaystyle \mathrm {mRMR} =\max _{S}\left[{\frac {1}{|S|}}\sum _{f_{i}\in S}I(f_{i};c)-{\frac {1}{|S|^{2}}}\sum _{f_{i},f_{j}\in S}I(f_{i};f_{j})\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eec7b98cd9e6fc9b3b61c0ac4712a16379c8859)


![{\displaystyle \mathrm {mRMR} =\max _{x\in \{0,1\}^{n}}\left[{\frac {\sum _{i=1}^{n}c_{i}x_{i}}{\sum _{i=1}^{n}x_{i}}}-{\frac {\sum _{i,j=1}^{n}a_{ij}x_{i}x_{j}}{(\sum _{i=1}^{n}x_{i})^{2}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0baef01e8c550ba917099a82e0ac43e826f59d37)

![{\displaystyle F_{n\times 1}=[I(f_{1};c),\ldots ,I(f_{n};c)]^{T}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e655a9d669fdf3ca7c6572563f8b5d1c1d7af44e)
![{\displaystyle H_{n\times n}=[I(f_{i};f_{j})]_{i,j=1\ldots n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5d1966a8fa8bd4894b5d768dcfc4da9b1caa9de)





![{\displaystyle {\begin{aligned}JMI(f_{i})&=\sum _{f_{j}\in S}(I(f_{i};c)+I(f_{i};c|f_{j}))\\&=\sum _{f_{j}\in S}{\bigl [}I(f_{j};c)+I(f_{i};c)-{\bigl (}I(f_{i};f_{j})-I(f_{i};f_{j}|c){\bigr )}{\bigr ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c44f7ace0374e11b551d8a9f254513a1cb431d1)






















![{\displaystyle \mathrm {CFS} =\max _{S_{k}}\left[{\frac {r_{cf_{1}}+r_{cf_{2}}+\cdots +r_{cf_{k}}}{\sqrt {k+2(r_{f_{1}f_{2}}+\cdots +r_{f_{i}f_{j}}+\cdots +r_{f_{k}f_{k-1}})}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83568ac8d01463888fbfb13c56c9dd32a790699e)


![{\displaystyle \mathrm {CFS} =\max _{x\in \{0,1\}^{n}}\left[{\frac {(\sum _{i=1}^{n}a_{i}x_{i})^{2}}{\sum _{i=1}^{n}x_{i}+\sum _{i\neq j}2b_{ij}x_{i}x_{j}}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9491bc46548bd4416952e59704e78388e8726480)
