Franklin graph
| Franklin Graph | |
|---|---|
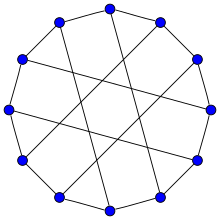 The Franklin Graph | |
| Named after | Philip Franklin |
| Vertices | 12 |
| Edges | 18 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 4 |
| Automorphisms | 48 (Z/2Z×S4) |
| Chromatic number | 2 |
| Chromatic index | 3 |
| Genus | 1 |
| Properties | Cubic Hamiltonian Bipartite Triangle-free Perfect Vertex-transitive |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Franklin graph is a 3-regular graph with 12 vertices and 18 edges.
The Franklin graph is named after Philip Franklin, who disproved the Heawood conjecture on the number of colors needed when a two-dimensional surface is partitioned into cells by a graph embedding.[1] The Heawood conjecture implied that the maximum chromatic number of a map on the Klein bottle should be seven, but Franklin proved that in this case six colors always suffice. (The Klein bottle is the only surface for which the Heawood conjecture fails.) The Franklin graph can be embedded in the Klein bottle so that it forms a map requiring six colors, showing that six colors are sometimes necessary in this case. This embedding is the Petrie dual of its embedding in the projective plane shown below.
It is Hamiltonian and has chromatic number 2, chromatic index 3, radius 3, diameter 3 and girth 4. It is also a 3-vertex-connected and 3-edge-connected perfect graph.
Algebraic properties
[edit]The automorphism group of the Franklin graph is of order 48 and is isomorphic to Z/2Z×S4, the direct product of the cyclic group Z/2Z and the symmetric group S4. It acts transitively on the vertices of the graph, making it vertex-transitive.
The characteristic polynomial of the Franklin graph is
Gallery
[edit]-
The chromatic number of the Franklin graph is 2.
-
The chromatic index of the Franklin graph is 3.
-
Alternative drawing of the Franklin graph.
-
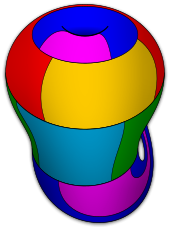
The Franklin graph embedded in the projective plane as the truncated hemi-octahedron.
References
[edit]- ^ Franklin, P. "A Six Color Problem." J. Math. Phys. 13, 363-379, 1934. doi:10.1002/sapm1934131363