Glossary of algebraic geometry
This is a glossary of algebraic geometry.
See also glossary of commutative algebra, glossary of classical algebraic geometry, and glossary of ring theory. For the number-theoretic applications, see glossary of arithmetic and Diophantine geometry.
For simplicity, a reference to the base scheme is often omitted; i.e., a scheme will be a scheme over some fixed base scheme S and a morphism an S-morphism.
!$@
[edit]- A generic point. For example, the point associated to the zero ideal for any integral affine scheme.
- F(n), F(D)
- 1. If X is a projective scheme with Serre's twisting sheaf and if F is an -module, then
- 2. If D is a Cartier divisor and F is an -module (X arbitrary), then If D is a Weil divisor and F is reflexive, then one replaces F(D) by its reflexive hull (and call the result still F(D).)
- |D|
- The complete linear system of a Weil divisor D on a normal complete variety X over an algebraically closed field k; that is, . There is a bijection between the set of k-rational points of |D| and the set of effective Weil divisors on X that are linearly equivalent to D.[1] The same definition is used if D is a Cartier divisor on a complete variety over k.
- [X/G]
- The quotient stack of, say, an algebraic space X by an action of a group scheme G.
- The GIT quotient of a scheme X by an action of a group scheme G.
- Ln
- An ambiguous notation. It usually means an n-th tensor power of L but can also mean the self-intersection number of L. If , the structure sheaf on X, then it means the direct sum of n copies of .
- The tautological line bundle. It is the dual of Serre's twisting sheaf .
- Serre's twisting sheaf. It is the dual of the tautological line bundle . It is also called the hyperplane bundle.
- 1. If D is an effective Cartier divisor on X, then it is the inverse of the ideal sheaf of D.
- 2. Most of the times, is the image of D under the natural group homomorphism from the group of Cartier divisors to the Picard group of X, the group of isomorphism classes of line bundles on X.
- 3. In general, is the sheaf corresponding to a Weil divisor D (on a normal scheme). It need not be locally free, only reflexive.
- 4. If D is a -divisor, then is of the integral part of D.
- 1. is the sheaf of Kähler differentials on X.
- 2. is the p-th exterior power of .
- 1. If p is 1, this is the sheaf of logarithmic Kähler differentials on X along D (roughly differential forms with simple poles along a divisor D.)
- 2. is the p-th exterior power of .
- P(V)
- The notation is ambiguous. Its traditional meaning is the projectivization of a finite-dimensional k-vector space V; i.e., (the Proj of the ring of polynomial functions k[V]) and its k-points correspond to lines in V. In contrast, Hartshorne and EGA write P(V) for the Proj of the symmetric algebra of V.
- Q-factorial
- A normal variety is -factorial if every -Weil divisor is -Cartier.
- Spec(R)
- The set of all prime ideals in a ring R with Zariski topology; it is called the prime spectrum of R.
- SpecX(F)
- The relative Spec of the OX-algebra F. It is also denoted by Spec(F) or simply Spec(F).
- Specan(R)
- The set of all valuations for a ring R with a certain weak topology; it is called the Berkovich spectrum of R.
A
[edit]- abelian
- 1. An abelian variety is a complete group variety. For example, consider the complex variety or an elliptic curve over a finite field .
- 2. An abelian scheme is a (flat) family of abelian varieties.
- adjunction formula
- 1. If D is an effective Cartier divisor on an algebraic variety X, both admitting dualizing sheaves , then the adjunction formula says: .
- 2. If, in addition, X and D are smooth, then the formula is equivalent to saying: where are canonical divisors on D and X.
- affine
- 1. Affine space is roughly a vector space where one has forgotten which point is the origin
- 2. An affine variety is a variety in affine space
- 3. An affine scheme is a scheme that is the prime spectrum of some commutative ring.
- 4. A morphism is called affine if the preimage of any open affine subset is again affine. In more fancy terms, affine morphisms are defined by the global Spec construction for sheaves of OX-Algebras, defined by analogy with the spectrum of a ring. Important affine morphisms are vector bundles, and finite morphisms.
- 5. The affine cone over a closed subvariety X of a projective space is the Spec of the homogeneous coordinate ring of X.
- algebraic geometry
- Algebraic geometry is a branch of mathematics that studies solutions to algebraic equations.
- algebraic geometry over the field with one element
- One goal is to prove the Riemann hypothesis.[2] See also the field with one element and Peña, Javier López; Lorscheid, Oliver (2009-08-31). "Mapping F_1-land:An overview of geometries over the field with one element". arXiv:0909.0069 [math.AG]. as well as [3][4] .
- algebraic group
- An algebraic group is an algebraic variety that is also a group in such a way the group operations are morphisms of varieties.
- algebraic scheme
- A separated scheme of finite type over a field. For example, an algebraic variety is a reduced irreducible algebraic scheme.
- algebraic set
- An algebraic set over a field k is a reduced separated scheme of finite type over . An irreducible algebraic set is called an algebraic variety.
- algebraic space
- An algebraic space is a quotient of a scheme by the étale equivalence relation.
- algebraic variety
- An algebraic variety over a field k is an integral separated scheme of finite type over . Note, not assuming k is algebraically closed causes some pathology; for example, is not a variety since the coordinate ring is not an integral domain.
- algebraic vector bundle
- A locally free sheaf of a finite rank.
- ample
- A line bundle on a projective variety is ample if some tensor power of it is very ample.
- Arakelov geometry
- Algebraic geometry over the compactification of Spec of the ring of rational integers . See Arakelov geometry.[5]
- arithmetic genus
- The arithmetic genus of a projective variety X of dimension r is .
- Artin stack
- Another term for an algebraic stack.
- artinian
- 0-dimensional and Noetherian. The definition applies both to a scheme and a ring.
Algebraic geometry occupied a central place in the mathematics of the last century. The deepest results of Abel, Riemann, Weierstrass, many of the most important papers of Klein and Poincare belong to this domain. At the end of the last and the beginning of the present century the attitude towards algebraic geometry changed abruptly. ... The style of thinking that was fully developed in algebraic geometry at that time was too far removed from the set-theoretical and axiomatic spirit, which then determined the development of mathematics. ... Around the middle of the present century algebraic geometry had undergone to a large extent such a reshaping process. As a result, it can again lay claim to the position it once occupied in mathematics.
From the preface to I.R. Shafarevich, Basic Algebraic Geometry.
B
[edit]- Behrend function
- The weighted Euler characteristic of a (nice) stack X with respect to the Behrend function is the degree of the virtual fundamental class of X.
- Behrend's trace formula
- Behrend's trace formula generalizes Grothendieck's trace formula; both formulas compute the trace of the Frobenius on l-adic cohomology.
- big
- A big line bundle L on X of dimension n is a line bundle such that .
- birational morphism
- A birational morphism between schemes is a morphism that becomes an isomorphism after restricted to some open dense subset. One of the most common examples of a birational map is the map induced by a blowup.
- blow-up
- A blow-up is a birational transformation that replaces a closed subscheme with an effective Cartier divisor. Precisely, given a noetherian scheme X and a closed subscheme , the blow-up of X along Z is a proper morphism such that (1) is an effective Cartier divisor, called the exceptional divisor and (2) is universal with respect to (1). Concretely, it is constructed as the relative Proj of the Rees algebra of with respect to the ideal sheaf determining Z.
C
[edit]- Calabi–Yau
- The Calabi–Yau metric is a Kähler metric whose Ricci curvature is zero.
- canonical
- 1. The canonical sheaf on a normal variety X of dimension n is where i is the inclusion of the smooth locus U and is the sheaf of differential forms on U of degree n. If the base field has characteristic zero instead of normality, then one may replace i by a resolution of singularities.
- 2. The canonical class on a normal variety X is the divisor class such that .
- 3. The canonical divisor is a representative of the canonical class denoted by the same symbol (and not well-defined.)
- 4. The canonical ring of a normal variety X is the section ring of the canonical sheaf.
- canonical model
- The canonical model is the Proj of a canonical ring (assuming the ring is finitely generated.)
- Cartier
- An effective Cartier divisor D on a scheme X over S is a closed subscheme of X that is flat over S and whose ideal sheaf is invertible (locally free of rank one).
- Castelnuovo–Mumford regularity
- The Castelnuovo–Mumford regularity of a coherent sheaf F on a projective space over a scheme S is the smallest integer r such that
- catenary
- A scheme is catenary, if all chains between two irreducible closed subschemes have the same length. Examples include virtually everything, e.g. varieties over a field, and it is hard to construct examples that are not catenary.
- central fiber
- A special fiber.
- Chow group
- The k-th Chow group of a smooth variety X is the free abelian group generated by closed subvarieties of dimension k (group of k-cycles) modulo rational equivalences.
- classification
- 1. Classification is a guiding principle in all of mathematics where one tries to describe all objects satisfying certain properties up to given equivalences by more accessible data such as invariants or even some constructive process. In algebraic geometry one distinguishes between discrete and continuous invariants. For continuous classifying invariants one additionally attempts to provide some geometric structure which leads to moduli spaces.
- 2. Complete smooth curves over an algebraically closed field are classified up to rational equivalence by their genus . (a) . rational curves, i.e. the curve is birational to the projective line . (b) . Elliptic curves, i.e. the curve is a complete 1-dimensional group scheme after choosing any point on the curve as identity. (c) . Hyperbolic curves, also called curves of general type. See algebraic curves for examples. The classification of smooth curves can be refined by the degree for projectively embedded curves, in particular when restricted to plane curves. Note that all complete smooth curves are projective in the sense that they admit embeddings into projective space, but for the degree to be well-defined a choice of such an embedding has to be explicitly specified. The arithmetic of a complete smooth curve over a number field (in particular number and structure of its rational points) is governed by the classification of the associated curve base changed to an algebraic closure. See Faltings's theorem for details on the arithmetic implications.
- 3. Classification of complete smooth surfaces over an algebraically closed field up to rational equivalence. See an overview of the classification or Enriques–Kodaira classification for details.
- 4. Classification of singularities resp. associated Zariski neighboorhoods over algebraically closed fields up to isomorphism. (a) In characteristic 0 Hironaka's resolution result attaches invariants to a singularity which classify them. (b) For curves and surfaces resolution is known in any characteristic which also yields a classification. See here for curves or here for curves and surfaces.
- 5. Classification of Fano varieties in small dimension.
- 6. The minimal model program is an approach to birational classification of complete smooth varieties in higher dimension (at least 2). While the original goal is about smooth varieties, terminal singularites naturally appear and are part of a wider classification.
- 7. Classification of split reductive groups up to isomorphism over algebraically closed fields.
- classifying stack
- An analog of a classifying space for torsors in algebraic geometry; see classifying stack.
- closed
- Closed subschemes of a scheme X are defined to be those occurring in the following construction. Let J be a quasi-coherent sheaf of -ideals. The support of the quotient sheaf is a closed subset Z of X and is a scheme called the closed subscheme defined by the quasi-coherent sheaf of ideals J.[6] The reason the definition of closed subschemes relies on such a construction is that, unlike open subsets, a closed subset of a scheme does not have a unique structure as a subscheme.
- Cohen–Macaulay
- A scheme is called Cohen-Macaulay
if all local rings are Cohen-Macaulay.
For example, regular schemes, and Spec k[x,y]/(xy) are Cohen–Macaulay, but
 is not.
is not. - coherent sheaf
- A coherent sheaf on a Noetherian scheme X is a quasi-coherent sheaf that is finitely generated as OX-module.
- conic
- An algebraic curve of degree two.
- connected
- The scheme is connected as a topological space. Since the connected components refine the irreducible components any irreducible scheme is connected but not vice versa. An affine scheme Spec(R) is connected iff the ring R possesses no idempotents other than 0 and 1; such a ring is also called a connected ring. Examples of connected schemes include affine space, projective space, and an example of a scheme that is not connected is Spec(k[x]×k[x])
- compactification
- See for example Nagata's compactification theorem.
- Cox ring
- A generalization of a homogeneous coordinate ring. See Cox ring.
- crepant
- A crepant morphism between normal varieties is a morphism such that .
- curve
- An algebraic variety of dimension one.
D
[edit]- deformation
- Let be a morphism of schemes and X an S-scheme. Then a deformation X' of X is an S'-scheme together with a pullback square in which X is the pullback of X' (typically X' is assumed to be flat).
- degeneracy locus
- Given a vector-bundle map over a variety X (that is, a scheme X-morphism between the total spaces of the bundles), the degeneracy locus is the (scheme-theoretic) locus .
- degeneration
- 1. A scheme X is said to degenerate to a scheme (called the limit of X) if there is a scheme with generic fiber X and special fiber .
- 2. A flat degeneration is a degeneration such that is flat.
- dimension
- The dimension, by definition the maximal length of a chain of irreducible closed subschemes, is a global property. It can be seen locally if a scheme is irreducible. It depends only on the topology, not on the structure sheaf. See also Global dimension. Examples: equidimensional schemes in dimension 0: Artinian schemes, 1: algebraic curves, 2: algebraic surfaces.
- degree
- 1. The degree of a line bundle L on a complete variety is an integer d such that .
- 2. If x is a cycle on a complete variety over a field k, then its degree is .
- 3. For the degree of a finite morphism, see morphism of varieties#Degree of a finite morphism.
- derived algebraic geometry
- An approach to algebraic geometry using (commutative) ring spectra instead of commutative rings; see derived algebraic geometry.
- divisorial
- 1. A divisorial sheaf on a normal variety is a reflexive sheaf of the form OX(D) for some Weil divisor D.
- 2. A divisorial scheme is a scheme admitting an ample family of invertible sheaves. A scheme admitting an ample invertible sheaf is a basic example.
- dominant
- A morphism f : X → Y is called dominant, if the image f(X) is dense. A morphism of affine schemes Spec A → Spec B is dense if and only if the kernel of the corresponding map B → A is contained in the nilradical of B.
- dualizing complex
- See Coherent duality.
- dualizing sheaf
- On a projective Cohen–Macaulay scheme of pure dimension n, the dualizing sheaf is a coherent sheaf on X such that holds for any locally free sheaf F on X; for example, if X is a smooth projective variety, then it is a canonical sheaf.
E
[edit]- Éléments de géométrie algébrique
- The EGA was an incomplete attempt to lay a foundation of algebraic geometry based on the notion of scheme, a generalization of an algebraic variety. Séminaire de géométrie algébrique picks up where the EGA left off. Today it is one of the standard references in algebraic geometry.
- elliptic curve
- An elliptic curve is a smooth projective curve of genus one.
- essentially of finite type
- Localization of a finite type scheme.
- étale
- A morphism f : Y → X is étale if it is flat and unramified. There are several other equivalent definitions. In the case of smooth varieties and over an algebraically closed field, étale morphisms are precisely those inducing an isomorphism of tangent spaces , which coincides with the usual notion of étale map in differential geometry. Étale morphisms form a very important class of morphisms; they are used to build the so-called étale topology and consequently the étale cohomology, which is nowadays one of the cornerstones of algebraic geometry.
- Euler sequence
- The exact sequence of sheaves:
- equivariant intersection theory
- See Chapter II of http://www.math.ubc.ca/~behrend/cet.pdf
F
[edit]- F-regular
- Related to Frobenius morphism.[7]
- Fano
- A Fano variety is a smooth projective variety X whose anticanonical sheaf is ample.
- fiber
- Given between schemes, the fiber of f over y is, as a set, the pre-image ; it has the natural structure of a scheme over the residue field of y as the fiber product , where has the natural structure of a scheme over Y as Spec of the residue field of y.
- fiber product
- 1. Another term for the "pullback" in the category theory.
- 2. A stack given for : an object over B is a triple (x, y, ψ), x in F(B), y in H(B), ψ an isomorphism in G(B); an arrow from (x, y, ψ) to (x', y', ψ') is a pair of morphisms such that . The resulting square with obvious projections does not commute; rather, it commutes up to natural isomorphism; i.e., it 2-commutes.
- final
- One of Grothendieck's fundamental ideas is to emphasize relative notions, i.e. conditions on morphisms rather than conditions on schemes themselves. The category of schemes has a final object, the spectrum of the ring of integers; so that any scheme is over , and in a unique way.
- finite
- The morphism f : Y → X is finite if may be covered by affine open sets such that each is affine — say of the form — and furthermore is finitely generated as a -module. See finite morphism. Finite morphisms are quasi-finite, but not all morphisms having finite fibers are quasi-finite, and morphisms of finite type are usually not quasi-finite.
- finite type (locally)
- The morphism f : Y → X is locally of finite type if may be covered by affine open sets such that each inverse image is covered by affine open sets where each is finitely generated as a -algebra. The morphism f : Y → X is of finite type if may be covered by affine open sets such that each inverse image is covered by finitely many affine open sets where each is finitely generated as a -algebra.
- finite fibers
- The morphism f : Y → X has finite fibers if the fiber over each point is a finite set. A morphism is quasi-finite if it is of finite type and has finite fibers.
- finite presentation
- If y is a point of Y, then the morphism f is of finite presentation at y (or finitely presented at y) if there is an open affine neighborhood U of f(y) and an open affine neighbourhood V of y such that f(V) ⊆ U and is a finitely presented algebra over . The morphism f is locally of finite presentation if it is finitely presented at all points of Y. If X is locally Noetherian, then f is locally of finite presentation if, and only if, it is locally of finite type.[8] The morphism f : Y → X is of finite presentation (or Y is finitely presented over X) if it is locally of finite presentation, quasi-compact, and quasi-separated. If X is locally Noetherian, then f is of finite presentation if, and only if, it is of finite type.[9]
- flag variety
- The flag variety parametrizes a flag of vector spaces.
- flat
- A morphism is flat if it gives rise to a flat map on stalks. When viewing a morphism f : Y → X as a family of schemes parametrized by the points of , the geometric meaning of flatness could roughly be described by saying that the fibers do not vary too wildly.
- formal
- See formal scheme.
G
[edit]- grd
- Given a curve C, a divisor D on it and a vector subspace , one says the linear system is a grd if V has dimension r+1 and D has degree d. One says C has a grd if there is such a linear system.
- Gabriel–Rosenberg reconstruction theorem
- The Gabriel–Rosenberg reconstruction theorem states a scheme X can be recovered from the category of quasi-coherent sheaves on X.[10] The theorem is a starting point for noncommutative algebraic geometry since, taking the theorem as an axiom, defining a noncommutative scheme amounts to defining the category of quasi-coherent sheaves on it. See also https://mathoverflow.net/q/16257
- G-bundle
- A principal G-bundle.
- generic point
- A dense point.
- genus
- See #arithmetic genus, #geometric genus.
- genus formula
- The genus formula for a nodal curve in the projective plane says the genus of the curve is given as where d is the degree of the curve and δ is the number of nodes (which is zero if the curve is smooth).
- geometric genus
- The geometric genus of a smooth projective variety X of dimension n is (where the equality is Serre's duality theorem.)
- geometric point
- The prime spectrum of an algebraically closed field.
- geometric property
- A property of a scheme X over a field k is "geometric" if it holds for for any field extension .
- geometric quotient
- The geometric quotient of a scheme X with the action of a group scheme G is a good quotient such that the fibers are orbits.
- gerbe
- A gerbe is (roughly) a stack that is locally nonempty and in which two objects are locally isomorphic.
- GIT quotient
- The GIT quotient is when and when .
- good quotient
- The good quotient of a scheme X with the action of a group scheme G is an invariant morphism such that
- Gorenstein
- 1. A Gorenstein scheme is a locally Noetherian scheme whose local rings are Gorenstein rings.
- 2. A normal variety is said to be -Gorenstein if the canonical divisor on it is -Cartier (and need not be Cohen–Macaulay).
- 3. Some authors call a normal variety Gorenstein if the canonical divisor is Cartier; note this usage is inconsistent with meaning 1.
- Grauert–Riemenschneider vanishing theorem
- The Grauert–Riemenschneider vanishing theorem extends the Kodaira vanishing theorem to higher direct image sheaves; see also https://arxiv.org/abs/1404.1827
- Grothendieck ring of varieties
- The Grothendieck ring of varieties is the free abelian group generated by isomorphism classes of varieties with the relation: where Z is a closed subvariety of a variety X and equipped with the multiplication
- Grothendieck's vanishing theorem
- Grothendieck's vanishing theorem concerns local cohomology.
- group scheme
- A group scheme is a scheme whose sets of points have the structures of a group.
- group variety
- An old term for a "smooth" algebraic group.
H
[edit]- Hilbert polynomial
- The Hilbert polynomial of a projective scheme X over a field is the Euler characteristic .
- Hodge bundle
- The Hodge bundle on the moduli space of curves (of fixed genus) is roughly a vector bundle whose fiber over a curve C is the vector space .
- hyperelliptic
- A curve is hyperelliptic if it has a g12 (i.e., there is a linear system of dimension 1 and degree 2.)
- hyperplane bundle
- Another term for Serre's twisting sheaf . It is the dual of the tautological line bundle (whence the term).
I
[edit]- image
- If f : Y → X is any morphism of schemes, the scheme-theoretic image of f is the unique closed subscheme i : Z → X which satisfies the following universal property: This notion is distinct from that of the usual set-theoretic image of f, f(Y). For example, the underlying space of Z always contains (but is not necessarily equal to) the Zariski closure of f(Y) in X, so if Y is any open (and not closed) subscheme of X and f is the inclusion map, then Z is different from f(Y). When Y is reduced, then Z is the Zariski closure of f(Y) endowed with the structure of reduced closed subscheme. But in general, unless f is quasi-compact, the construction of Z is not local on X.
- immersion
- Immersions f : Y → X are maps that factor through isomorphisms with subschemes. Specifically, an open immersion factors through an isomorphism with an open subscheme and a closed immersion factors through an isomorphism with a closed subscheme.[13] Equivalently, f is a closed immersion if, and only if, it induces a homeomorphism from the underlying topological space of Y to a closed subset of the underlying topological space of X, and if the morphism is surjective.[14] A composition of immersions is again an immersion.[15] Some authors, such as Hartshorne in his book Algebraic Geometry and Q. Liu in his book Algebraic Geometry and Arithmetic Curves, define immersions as the composite of an open immersion followed by a closed immersion. These immersions are immersions in the sense above, but the converse is false. Furthermore, under this definition, the composite of two immersions is not necessarily an immersion. However, the two definitions are equivalent when f is quasi-compact.[16] Note that an open immersion is completely described by its image in the sense of topological spaces, while a closed immersion is not: and may be homeomorphic but not isomorphic. This happens, for example, if I is the radical of J but J is not a radical ideal. When specifying a closed subset of a scheme without mentioning the scheme structure, usually the so-called reduced scheme structure is meant, that is, the scheme structure corresponding to the unique radical ideal consisting of all functions vanishing on that closed subset.
- ind-scheme
- An ind-scheme is an inductive limit of closed immersions of schemes.
- invertible sheaf
- A locally free sheaf of a rank one. Equivalently, it is a torsor for the multiplicative group (i.e., line bundle).
- integral
- A scheme that is both reduced and irreducible is called integral. For locally Noetherian schemes, to be integral is equivalent to being a connected scheme that is covered by the spectra of integral domains. (Strictly speaking, this is not a local property, because the disjoint union of two integral schemes is not integral. However, for irreducible schemes, it is a local property.) For example, the scheme Spec k[t]/f, f irreducible polynomial is integral, while Spec A×B (A, B ≠ 0) is not.
- irreducible
- A scheme X is said to be irreducible when (as a topological space) it is not the union of two closed subsets except if one is equal to X. Using the correspondence of prime ideals and points in an affine scheme, this means X is irreducible iff X is connected and the rings Ai all have exactly one minimal prime ideal. (Rings possessing exactly one minimal prime ideal are therefore also called irreducible.) Any noetherian scheme can be written uniquely as the union of finitely many maximal irreducible non-empty closed subsets, called its irreducible components. Affine space and projective space are irreducible, while
Spec k[x,y]/(xy) =
 is not.
is not.
J
[edit]- Jacobian variety
- The Jacobian variety of a projective curve X is the degree zero part of the Picard variety .
K
[edit]- Kempf vanishing theorem
- The Kempf vanishing theorem concerns the vanishing of higher cohomology of a flag variety.
- klt
- Abbreviation for "kawamata log terminal"
- Kodaira dimension
- 1. The Kodaira dimension (also called the Iitaka dimension) of a semi-ample line bundle L is the dimension of Proj of the section ring of L.
- 2. The Kodaira dimension of a normal variety X is the Kodaira dimension of its canonical sheaf.
- Kodaira vanishing theorem
- See the Kodaira vanishing theorem.
- Kuranishi map
- See Kuranishi structure.
L
[edit]- Lelong number
- See Lelong number.
- level structure
- see http://math.stanford.edu/~conrad/248BPage/handouts/level.pdf
- linearization
- Another term for the structure of an equivariant sheaf/vector bundle.
- local
- Most important properties of schemes are local in nature, i.e. a scheme X has a certain property P if and only if for any cover of X by open subschemes Xi, i.e. X= Xi, every Xi has the property P. It is usually the case that it is enough to check one cover, not all possible ones. One also says that a certain property is Zariski-local, if one needs to distinguish between the Zariski topology and other possible topologies, like the étale topology. Consider a scheme X and a cover by affine open subschemes Spec Ai. Using the dictionary between (commutative) rings and affine schemes local properties are thus properties of the rings Ai. A property P is local in the above sense, iff the corresponding property of rings is stable under localization. For example, we can speak of locally Noetherian schemes, namely those which are covered by the spectra of Noetherian rings. The fact that localizations of a Noetherian ring are still noetherian then means that the property of a scheme of being locally Noetherian is local in the above sense (whence the name). Another example: if a ring is reduced (i.e., has no non-zero nilpotent elements), then so are its localizations. An example for a non-local property is separatedness (see below for the definition). Any affine scheme is separated, therefore any scheme is locally separated. However, the affine pieces may glue together pathologically to yield a non-separated scheme. The following is a (non-exhaustive) list of local properties of rings, which are applied to schemes. Let X = Spec Ai be a covering of a scheme by open affine subschemes. For definiteness, let k denote a field in the following. Most of the examples also work with the integers Z as a base, though, or even more general bases. Connected, irreducible, reduced, integral, normal, regular, Cohen-Macaulay, locally noetherian, dimension, catenary, Gorenstein.
- local complete intersection
- The local rings are complete intersection rings. See also: regular embedding.
- local uniformization
- The local uniformization is a method of constructing a weaker form of resolution of singularities by means of valuation rings.
- locally factorial
- The local rings are unique factorization domains.
- locally of finite presentation
- Cf. finite presentation above.
- locally of finite type
- The morphism f : Y → X is locally of finite type if may be covered by affine open sets such that each inverse image is covered by affine open sets where each is finitely generated as a -algebra.
- locally Noetherian
- The Ai are Noetherian rings. If in addition a finite number of such affine spectra covers X, the scheme is called noetherian. While it is true that the spectrum of a noetherian ring is a noetherian topological space, the converse is false. For example, most schemes in finite-dimensional algebraic geometry are locally Noetherian, but is not.
- logarithmic geometry
- log structure
- See log structure. The notion is due to Fontaine-Illusie and Kato.
- loop group
- See loop group (the linked article does not discuss a loop group in algebraic geometry; for now see also ind-scheme).
M
[edit]- moduli
- See for example moduli space.
While much of the early work on moduli, especially since [Mum65], put the emphasis on the construction of fine or coarse moduli spaces, recently the emphasis shifted towards the study of the families of varieties, that is towards moduli functors and moduli stacks. The main task is to understand what kind of objects form "nice" families. Once a good concept of "nice families" is established, the existence of a coarse moduli space should be nearly automatic. The coarse moduli space is not the fundamental object any longer, rather it is only a convenient way to keep track of certain information that is only latent in the moduli functor or moduli stack.
Kollár, János, Chapter 1, "Book on Moduli of Surfaces".
- Mori's minimal model program
- The minimal model program is a research program aiming to do birational classification of algebraic varieties of dimension greater than 2.
- morphism
- 1. A morphism of algebraic varieties is given locally by polynomials.
- 2. A morphism of schemes is a morphism of locally ringed spaces.
- 3. A morphism of stacks (over, say, the category of S-schemes) is a functor such that where are structure maps to the base category.
N
[edit]- nef
- See nef line bundle.
- nonsingular
- An archaic term for "smooth" as in a smooth variety.
- normal
- 1. An integral scheme is called normal, if the local rings are integrally closed domains. For example, all regular schemes are normal, while singular curves are not.
- 2. A smooth curve is said to be k-normal if the hypersurfaces of degree k cut out the complete linear series . It is projectively normal if it is k-normal for all k > 0. One thus says that "a curve is projectively normal if the linear system that embeds it is complete." The term "linearly normal" is synonymous with 1-normal.
- 3. A closed subvariety is said to be projectively normal if the affine cover over X is a normal scheme; i.e., the homogeneous coordinate ring of X is an integrally closed domain. This meaning is consistent with that of 2.
- normal
- 1. If X is a closed subscheme of a scheme Y with ideal sheaf I, then the normal sheaf to X is . If the embedded of X into Y is regular, it is locally free and is called the normal bundle.
- 2. The normal cone to X is . if X is regularly embedded into Y, then the normal cone is isomorphic to , the total space of the normal bundle to X.
- normal crossings
- Abbreviations nc for normal crossing and snc for simple normal crossing. Refers to several closely related notions such as nc divisor, nc singularity, snc divisor, and snc singularity. See normal crossings.
- normally generated
- A line bundle L on a variety X is said to be normally generated if, for each integer n > 0, the natural map is surjective.
O
[edit]- open
- 1. A morphism f : Y → X of schemes is called open (closed), if the underlying map of topological spaces is open (closed, respectively), i.e. if open subschemes of Y are mapped to open subschemes of X (and similarly for closed). For example, finitely presented flat morphisms are open and proper maps are closed.
- 2. An open subscheme of a scheme X is an open subset U with structure sheaf .[14]
- orbifold
- Nowadays an orbifold is often defined as a Deligne–Mumford stack over the category of differentiable manifolds.[17]
P
[edit]- p-divisible group
- See p-divisible group (roughly an analog of torsion points of an abelian variety).
- pencil
- A linear system of dimension one.
- Picard group
- The Picard group of X is the group of the isomorphism classes of line bundles on X, the multiplication being the tensor product.
- Plücker embedding
- The Plücker embedding is the closed embedding of the Grassmannian variety into a projective space.
- plurigenus
- The n-th plurigenus of a smooth projective variety is . See also Hodge number.
- Poincaré residue map
- See Poincaré residue.
- point
- A scheme is a locally ringed space, so a fortiori a topological space, but the meanings of point of are threefold:
- a point of the underlying topological space;
- a -valued point of is a morphism from to , for any scheme ;
- a geometric point, where is defined over (is equipped with a morphism to) , where is a field, is a morphism from to where is an algebraic closure of .
- polarization
- an embedding into a projective space
- Proj
- See Proj construction.
- projection formula
- The projection formula says that, for a morphism of schemes, an -module and a locally free -module of finite rank, there is a natural isomorphism (in short, is linear with respect to the action of locally free sheaves.)
- projective
- 1. A projective variety is a closed subvariety of a projective space.
- 2. A projective scheme over a scheme S is an S-scheme that factors through some projective space as a closed subscheme.
- 3. Projective morphisms are defined similarly to affine morphisms: f : Y → X is called projective if it factors as a closed immersion followed by the projection of a projective space to .[18] Note that this definition is more restrictive than that of EGA, II.5.5.2. The latter defines to be projective if it is given by the global Proj of a quasi-coherent graded OX-Algebra such that is finitely generated and generates the algebra . Both definitions coincide when is affine or more generally if it is quasi-compact, separated and admits an ample sheaf,[19] e.g. if is an open subscheme of a projective space over a ring .
- projective bundle
- If E is a locally free sheaf on a scheme X, the projective bundle P(E) of E is the global Proj of the symmetric algebra of the dual of E: Note this definition is standard nowadays (e.g., Fulton's Intersection theory) but differs from EGA and Hartshorne (they don't take a dual).
- projectively normal
- See #normal.
- proper
- A morphism is proper if it is separated, universally closed (i.e. such that fiber products with it are closed maps), and of finite type. Projective morphisms are proper; but the converse is not in general true. See also complete variety. A deep property of proper morphisms is the existence of a Stein factorization, namely the existence of an intermediate scheme such that a morphism can be expressed as one with connected fibres, followed by a finite morphism.
- property P
- Let P be a property of a scheme that is stable under base change (finite-type, proper, smooth, étale, etc.). Then a representable morphism is said to have property P if, for any with B a scheme, the base change has property P.
- pseudo-reductive
- Pseudoreductive generalizes reductive in the context of connected smooth linear algebraic group.
- pure dimension
- A scheme has pure dimension d if each irreducible component has dimension d.
Q
[edit]- quasi-coherent
- A quasi-coherent sheaf on a Noetherian scheme X is a sheaf of OX-modules that is locally given by modules.
- quasi-compact
- A morphism f : Y → X is called quasi-compact, if for some (equivalently: every) open affine cover of X by some Ui = Spec Bi, the preimages f−1(Ui) are quasi-compact.
- quasi-finite
- The morphism f : Y → X has finite fibers if the fiber over each point is a finite set. A morphism is quasi-finite if it is of finite type and has finite fibers.
- quasi-projective
- A quasi-projective variety is a locally closed subvariety of a projective space.
- quasi-separated
- A morphism f : Y → X is called quasi-separated or (Y is quasi-separated over X) if the diagonal morphism Y → Y ×XY is quasi-compact. A scheme Y is called quasi-separated if Y is quasi-separated over Spec(Z).[20]
- quasi-split
- A reductive group defined over a field is quasi-split if and only if it admits a Borel subgroup defined over . Any quasi-split reductive group is a split-reductive reductive group, but there are quasi-split reductive groups that are not split-reductive.
- Quot scheme
- A Quot scheme parametrizes quotients of locally free sheaves on a projective scheme.
- quotient stack
- Usually denoted by [X/G], a quotient stack generalizes a quotient of a scheme or variety.
R
[edit]- rational
- 1. Over an algebraically closed field, a variety is rational if it is birational to a projective space. For example, rational curves and rational surfaces are those birational to .
- 2. Given a field k and a relative scheme X → S, a k-rational point of X is an S-morphism .
- rational function
- An element in the function field where the limit runs over all coordinates rings of open subsets U of an (irreducible) algebraic variety X. See also function field (scheme theory).
- rational normal curve
- A rational normal curve is the image of . If d = 3, it is also called the twisted cubic.
- rational singularities
- A variety X over a field of characteristic zero has rational singularities if there is a resolution of singularities such that and .
- reduced
- 1. A commutative ring is reduced if it has no nonzero nilpotent elements, i.e., its nilradical is the zero ideal, . Equivalently, is reduced if is a reduced scheme.
- 2. A scheme X is reduced if its stalks are reduced rings. Equivalently X is reduced if, for each open subset , is a reduced ring, i.e., has no nonzero nilpotent sections.
- reductive
- A connected linear algebraic group over a field is a reductive group if and only if the unipotent radical of the base change of to an algebraic closure is trivial.
- reflexive sheaf
- A coherent sheaf is reflexive if the canonical map to the second dual is an isomorphism.
- regular
- A regular scheme is a scheme where the local rings are regular local rings. For example, smooth varieties over a field are regular, while
Spec k[x,y]/(x2+x3-y2)=
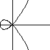 is not.
is not. - regular embedding
- A closed immersion is a regular embedding if each point of X has an affine neighborhood in Y so that the ideal of X there is generated by a regular sequence. If i is a regular embedding, then the conormal sheaf of i, that is, when is the ideal sheaf of X, is locally free.
- regular function
- A morphism from an algebraic variety to the affine line.
- representable morphism
- A morphism of stacks such that, for any morphism from a scheme B, the base change is an algebraic space. If "algebraic space" is replaced by "scheme", then it is said to be strongly representable.
- resolution of singularities
- A resolution of singularities of a scheme X is a proper birational morphism such that Z is smooth.
- Riemann–Hurwitz formula
- Given a finite separable morphism between smooth projective curves, if is tamely ramified (no wild ramification), for example, over a field of characteristic zero, then the Riemann–Hurwitz formula relates the degree of π, the genera of X, Y and the ramification indices: . Nowadays, the formula is viewed as a consequence of the more general formula (which is valid even if π is not tame): where means a linear equivalence and is the divisor of the relative cotangent sheaf (called the different).
- Riemann–Roch formula
- 1. If L is a line bundle of degree d on a smooth projective curve of genus g, then the Riemann–Roch formula computes the Euler characteristic of L: . For example, the formula implies the degree of the canonical divisor K is 2g - 2.
- 2. The general version is due to Grothendieck and called the Grothendieck–Riemann–Roch formula. It says: if is a proper morphism with smooth X, S and if E is a vector bundle on X, then as equality in the rational Chow group where , means a Chern character and a Todd class of the tangent bundle of a space, and, over the complex numbers, is an integration along fibers. For example, if the base S is a point, X is a smooth curve of genus g and E is a line bundle L, then the left-hand side reduces to the Euler characteristic while the right-hand side is
- rigid
- Every infinitesimal deformation is trivial. For example, the projective space is rigid since (and using the Kodaira–Spencer map).
- rigidify
- A heuristic term, roughly equivalent to "killing automorphisms". For example, one might say "we introduce level structures resp. marked points to rigidify the geometric situation."
S
[edit]- scheme
- A scheme is a locally ringed space that is locally a prime spectrum of a commutative ring.
- Schubert
- 1. A Schubert cell is a B-orbit on the Grassmannian where B is the standard Borel; i.e., the group of upper triangular matrices.
- 2. A Schubert variety is the closure of a Schubert cell.
- scroll
- A rational normal scroll is a ruled surface which is of degree in a projective space for some .
- secant variety
- The secant variety to a projective variety is the closure of the union of all secant lines to V in .
- section ring
- The section ring or the ring of sections of a line bundle L on a scheme X is the graded ring .
- Serre's conditions Sn
- See Serre's conditions on normality. See also https://mathoverflow.net/q/22228
- Serre duality
- See #dualizing sheaf
- separated
- A separated morphism is a morphism such that the fiber product of with itself along has its diagonal as a closed subscheme — in other words, the diagonal morphism is a closed immersion.
- sheaf generated by global sections
- A sheaf with a set of global sections that span the stalk of the sheaf at every point. See Sheaf generated by global sections.
- simple
- 1. The term "simple point" is an old term for a "smooth point".
- 2. A simple normal crossing (snc) divisor is another name for a smooth normal crossing divisor, i.e. a divisor that has only smooth normal crossing singularities. They appear in strong desingularization as well as in stabilization for compactifying moduli problems.
- 3. In the context of linear algebraic groups there are semisimple groups and simple groups which are themselves semisimple groups with additional properties. Since all simple groups are reductive, a split simple group is a simple group that is split-reductive.
- smooth
- 1.
The higher-dimensional analog of étale morphisms are smooth morphisms. There are many different characterisations of smoothness. The following are equivalent definitions of smoothness of the morphism f : Y → X:
- for any y ∈ Y, there are open affine neighborhoods V and U of y, x=f(y), respectively, such that the restriction of f to V factors as an étale morphism followed by the projection of affine n-space over U.
- f is flat, locally of finite presentation, and for every geometric point of Y (a morphism from the spectrum of an algebraically closed field to Y), the geometric fiber is a smooth n-dimensional variety over in the sense of classical algebraic geometry.
- 2. A smooth scheme over a perfect field k is a scheme X that is locally of finite type and regular over k.
- 3. A smooth scheme over a field k is a scheme X that is geometrically smooth: is smooth.
- special
- A divisor D on a smooth curve C is special if , which is called the index of speciality, is positive.
- spherical variety
- A spherical variety is a normal G-variety (G connected reductive) with an open dense orbit by a Borel subgroup of G.
- split
- 1. In the context of an algebraic group for certain properties there is the derived property split-. Usually is a property that is automatic or more common over algebraically closed fields . If this property holds already for defined over a not necessarily algebraically closed field then is said to satisfy split-.
- 2. A linear algebraic group defined over a field is a torus if only if its base change to an algebraic closure is isomorphic to a product of multiplicative groups . is a split torus if and only if it is isomorphic to without any base change. is said to split over an intermediate field if and only if its base change to is isomorphic to .
- 3. A reductive group defined over a field is split-reductive if and only if a maximal torus defined over is a split torus. Since any simple group is reductive a split simple group means a simple group that is split-reductive.
- 4. A connected solvable linear algebraic group defined over a field is split if and only if it has composition series defined over such that each successive quotient is isomorphic to either the multiplicative group or the additive group over .
- 5. A linear algebraic group defined over a field is split if and only if it has a Borel subgroup defined over that is split in the sense of connected solvable linear algebraic groups.
- 6. In the classification of real Lie algebras split Lie algebras play an important role. There is a close connection between linear Lie groups, their associated Lie algebras and linear algebraic groups over resp. . The term split has similar meanings for Lie theory and linear algebraic groups.
- stable
- 1. A stable curve is a curve with some "mild" singularity, used to construct a good-behaving moduli space of curves.
- 2. A stable vector bundle is used to construct the moduli space of vector bundles.
- stack
- A stack parametrizes sets of points together with automorphisms.
- strict transform
- Given a blow-up along a closed subscheme Z and a morphism , the strict transform of Y (also called proper transform) is the blow-up of Y along the closed subscheme . If f is a closed immersion, then the induced map is also a closed immersion.
- subscheme
- A subscheme, without qualifier, of X is a closed subscheme of an open subscheme of X.
- surface
- An algebraic variety of dimension two.
- symmetric variety
- An analog of a symmetric space. See symmetric variety.
On Grothendieck's own view there should be almost no history of schemes, but only a history of the resistance to them: ... There is no serious historical question of how Grothendieck found his definition of schemes. It was in the air. Serre has well said that no one invented schemes (conversation 1995). The question is, what made Grothendieck believe he should use this definition to simplify an 80 page paper by Serre into some 1000 pages of Éléments de géométrie algébrique?
T
[edit]- tangent space
- See Zariski tangent space.
- tautological line bundle
- The tautological line bundle of a projective scheme X is the dual of Serre's twisting sheaf ; that is, .
- theorem
- See Zariski's main theorem, theorem on formal functions, cohomology base change theorem, Category:Theorems in algebraic geometry.
- torus embedding
- An old term for a toric variety
- toric variety
- A toric variety is a normal variety with the action of a torus such that the torus has an open dense orbit.
- tropical geometry
- A kind of a piecewise-linear algebraic geometry. See tropical geometry.
- torus
- A split torus is a product of finitely many multiplicative groups .
U
[edit]- universal
- 1. If a moduli functor F is represented by some scheme or algebraic space M, then a universal object is an element of F(M) that corresponds to the identity morphism M → M (which is an M-point of M). If the values of F are isomorphism classes of curves with extra structure, say, then a universal object is called a universal curve. A tautological bundle would be another example of a universal object.
- 2. Let be the moduli of smooth projective curves of genus g and that of smooth projective curves of genus g with single marked points. In literature, the forgetful map is often called a universal curve.
- universally
- A morphism has some property universally if all base changes of the morphism have this property. Examples include universally catenary, universally injective.
- unramified
- For a point in , consider the corresponding morphism of local rings . Let be the maximal ideal of , and let be the ideal generated by the image of in . The morphism is unramified (resp. G-unramified) if it is locally of finite type (resp. locally of finite presentation) and if for all in , is the maximal ideal of and the induced map is a finite separable field extension.[21] This is the geometric version (and generalization) of an unramified field extension in algebraic number theory.
V
[edit]- variety
- a synonym with "algebraic variety".
- very ample
- A line bundle L on a variety X is very ample if X can be embedded into a projective space so that L is the restriction of Serre's twisting sheaf O(1) on the projective space.
W
[edit]- weakly normal
- a scheme is weakly normal if any finite birational morphism to it is an isomorphism.
- Weil divisor
- Another but more standard term for a "codimension-one cycle"; see divisor.
- Weil reciprocity
- See Weil reciprocity.
Z
[edit]- Zariski–Riemann space
- A Zariski–Riemann space is a locally ringed space whose points are valuation rings.
Notes
[edit]- ^ Proof: Let D be a Weil divisor on X. If D' ~ D, then there is a nonzero rational function f on X such that D + (f) = D' and then f is a section of OX(D) if D' is effective. The opposite direction is similar. □
- ^ Alain, Connes (2015-09-18). "An essay on the Riemann Hypothesis". arXiv:1509.05576 [math.NT].
- ^ Deitmar, Anton (2006-05-16). "Remarks on zeta functions and K-theory over F1". arXiv:math/0605429.
- ^ Flores, Jaret (2015-03-08). "Homological Algebra for Commutative Monoids". arXiv:1503.02309 [math.KT].
- ^ Durov, Nikolai (2007-04-16). "New Approach to Arakelov Geometry". arXiv:0704.2030 [math.AG].
- ^ Grothendieck & Dieudonné 1960, 4.1.2 and 4.1.3
- ^ Smith, Karen E.; Zhang, Wenliang (2014-09-03). "Frobenius Splitting in Commutative Algebra". arXiv:1409.1169 [math.AC].
- ^ Grothendieck & Dieudonné 1964, §1.4
- ^ Grothendieck & Dieudonné 1964, §1.6
- ^ Brandenburg, Martin (2014-10-07). "Tensor categorical foundations of algebraic geometry". arXiv:1410.1716 [math.AG].
- ^ Hartshorne 1977, Exercise II.3.11(d)
- ^ The Stacks Project, Chapter 21, §4.
- ^ Grothendieck & Dieudonné 1960, 4.2.1
- ^ a b Hartshorne 1977, §II.3
- ^ Grothendieck & Dieudonné 1960, 4.2.5
- ^ Q. Liu, Algebraic Geometry and Arithmetic Curves, exercise 2.3
- ^ Harada, Megumi; Krepski, Derek (2013-02-02). "Global quotients among toric Deligne-Mumford stacks". arXiv:1302.0385 [math.DG].
- ^ Hartshorne 1977, II.4
- ^ EGA, II.5.5.4(ii).
- ^ Grothendieck & Dieudonné 1964, 1.2.1
- ^ The notion G-unramified is what is called "unramified" in EGA, but we follow Raynaud's definition of "unramified", so that closed immersions are unramified. See Tag 02G4 in the Stacks Project for more details.
References
[edit]- Fulton, William (1998), Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], vol. 2, Berlin, New York: Springer-Verlag, doi:10.1007/978-1-4612-1700-8, ISBN 978-3-540-62046-4, MR 1644323
- Grothendieck, Alexandre; Dieudonné, Jean (1960). "Éléments de géométrie algébrique: I. Le langage des schémas". Publications Mathématiques de l'IHÉS. 4. doi:10.1007/bf02684778. MR 0217083.
- Grothendieck, Alexandre; Dieudonné, Jean (1961). "Éléments de géométrie algébrique: II. Étude globale élémentaire de quelques classes de morphismes". Publications Mathématiques de l'IHÉS. 8. doi:10.1007/bf02699291. MR 0217084.
- Grothendieck, Alexandre; Dieudonné, Jean (1961). "Eléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Première partie". Publications Mathématiques de l'IHÉS. 11. doi:10.1007/bf02684274. MR 0217085.
- Grothendieck, Alexandre; Dieudonné, Jean (1963). "Éléments de géométrie algébrique: III. Étude cohomologique des faisceaux cohérents, Seconde partie". Publications Mathématiques de l'IHÉS. 17. doi:10.1007/bf02684890. MR 0163911.
- Grothendieck, Alexandre; Dieudonné, Jean (1964). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Première partie". Publications Mathématiques de l'IHÉS. 20. doi:10.1007/bf02684747. MR 0173675.
- Grothendieck, Alexandre; Dieudonné, Jean (1965). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Seconde partie". Publications Mathématiques de l'IHÉS. 24. doi:10.1007/bf02684322. MR 0199181.
- Grothendieck, Alexandre; Dieudonné, Jean (1966). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Troisième partie". Publications Mathématiques de l'IHÉS. 28. doi:10.1007/bf02684343. MR 0217086.
- Grothendieck, Alexandre; Dieudonné, Jean (1967). "Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas, Quatrième partie". Publications Mathématiques de l'IHÉS. 32. doi:10.1007/bf02732123. MR 0238860.
- Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics, vol. 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157
- Kollár, János, "Book on Moduli of Surfaces" available at his website [2]
- Martin's Olsson's course notes written by Anton, https://web.archive.org/web/20121108104319/http://math.berkeley.edu/~anton/written/Stacks/Stacks.pdf
- A book worked out by many authors.

















![{\displaystyle \mathbf {P} (V)=\operatorname {Proj} (k[V])=\operatorname {Proj} (\operatorname {Sym} (V^{*}))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/761b2cd8fb1f3b6c3635fd24a97b6a17df7478ec)

















































































![{\displaystyle [X]=[Z]+[X-Z]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94ceffda5addfce38b335e080c7105629d78d5f1)
![{\displaystyle [X]\cdot [Y]=[X\times Y].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed9e5afec472fee8ab4c2700c0f4be0b1fa3fb38)















































![{\displaystyle k(X)=\varinjlim k[U]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/602ba53bdaff43c703fecdb34e4a8bbda33ece1d)









































































