Hydraulic pump

A hydraulic pump is a mechanical source of power that converts mechanical power into hydraulic energy (hydrostatic energy i.e. flow, pressure). Hydraulic pumps are used in hydraulic drive systems and can be hydrostatic or hydrodynamic. They generate flow with enough power to overcome pressure induced by a load at the pump outlet. When a hydraulic pump operates, it creates a vacuum at the pump inlet, which forces liquid from the reservoir into the inlet line to the pump and by mechanical action delivers this liquid to the pump outlet and forces it into the hydraulic system. Hydrostatic pumps are positive displacement pumps while hydrodynamic pumps can be fixed displacement pumps, in which the displacement (flow through the pump per rotation of the pump) cannot be adjusted, or variable displacement pumps, which have a more complicated construction that allows the displacement to be adjusted. Hydrodynamic pumps are more frequent in day-to-day life. Hydrostatic pumps of various types all work on the principle of Pascal's law.
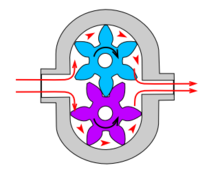
Types of hydraulic pump
[edit]Gear pumps
[edit]
Gear pumps (with external teeth) (fixed displacement) are simple and economical pumps. The swept volume or displacement of gear pumps for hydraulics will be between about 1 to 200 milliliters. They have the lowest volumetric efficiency ( ) of all three basic pump types (gear, vane and piston pumps)[1] These pumps create pressure through the meshing of the gear teeth, which forces fluid around the gears to pressurize the outlet side. Some gear pumps can be quite noisy, compared to other types, but modern gear pumps are highly reliable and much quieter than older models. This is in part due to designs incorporating split gears, helical gear teeth and higher precision/quality tooth profiles that mesh and unmesh more smoothly, reducing pressure ripple and related detrimental problems. Another positive attribute of the gear pump, is that catastrophic breakdown is a lot less common than in most other types of hydraulic pumps. This is because the gears gradually wear down the housing and/or main bushings, reducing the volumetric efficiency of the pump gradually until it is all but useless. This often happens long before wear and causes the unit to seize or break down. Hydraulic gear pumps are used in various applications where there are different requirements such as lifting, lowering, opening, closing, or rotating, and they are expected to be safe and long-lasting.[2]

Rotary vane pumps
[edit]
A rotary vane pump is a positive-displacement pump that consists of vanes mounted to a rotor that rotates inside a cavity. In some cases these vanes can have variable length and/or be tensioned to maintain contact with the walls as the pump rotates. A critical element in vane pump design is how the vanes are pushed into contact with the pump housing, and how the vane tips are machined at this very point. Several type of "lip" designs are used, and the main objective is to provide a tight seal between the inside of the housing and the vane, and at the same time to minimize wear and metal-to-metal contact. Forcing the vane out of the rotating centre and towards the pump housing is accomplished using spring-loaded vanes, or more traditionally, vanes loaded hydrodynamically (via the pressurized system fluid).[3]
Screw pumps
[edit]
Screw pumps (fixed displacement) consist of two Archimedes' screws that intermesh and are enclosed within the same chamber. These pumps are used for high flows at relatively low pressure (max 100 bars (10,000 kPa)).[clarification needed] They were used on board ships where a constant pressure hydraulic system extended through the whole ship, especially to control ball valves[clarification needed] but also to help drive the steering gear and other systems. The advantage of the screw pumps is the low sound level of these pumps; however, the efficiency is not high.
The major problem of screw pumps is that the hydraulic reaction force is transmitted in a direction that's axially opposed to the direction of the flow.
There are two ways to overcome this problem:
- put a thrust bearing beneath each rotor;
- create a hydraulic balance by directing a hydraulic force to a piston under the rotor.
Types of screw pumps:
- single end
- double end
- single rotor
- multi rotor timed
- multi rotor untimed.
Bent axis pumps
[edit]Bent axis pumps, axial piston pumps and motors using the bent axis principle, fixed or adjustable displacement, exists in two different basic designs. The Thoma-principle (engineer Hans Thoma, Germany, patent 1935) with max 25 degrees angle and the Wahlmark-principle (Gunnar Axel Wahlmark, patent 1960) with spherical-shaped pistons in one piece with the piston rod, piston rings, and maximum 40 degrees between the driveshaft centerline and pistons (Volvo Hydraulics Co.). These have the best efficiency of all pumps. Although in general, the largest displacements are approximately one litre per revolution, if necessary a two-liter swept volume pump can be built. Often variable-displacement pumps are used so that the oil flow can be adjusted carefully. These pumps can in general work with a working pressure of up to 350–420 bars in continuous work.
Inline axial piston pumps
[edit]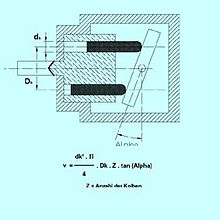
By using different compensation techniques, the variable displacement type of these pumps can continuously alter fluid discharge per revolution and system pressure based on load requirements, maximum pressure cut-off settings, horsepower/ratio control, and even fully electro proportional systems, requiring no other input than electrical signals. This makes them potentially hugely power saving compared to other constant flow pumps in systems where prime mover/diesel/electric motor rotational speed is constant and required fluid flow is non-constant.[4]
Radial piston pumps
[edit]
A radial piston pump is a form of hydraulic pump. The working pistons extend in a radial direction symmetrically around the drive shaft, in contrast to the axial piston pump.
Hydraulic pumps, calculation formulas
[edit]Flow
[edit]
where
- , flow (m3/s)
- , stroke frequency (Hz)
- , stroked volume (m3)
- , volumetric efficiency
Power
[edit]
where
- , power (W)
- , stroke frequency (Hz)
- , stroked volume (m3)
- , pressure difference over pump (Pa)
- , mechanical/hydraulic efficiency
Mechanical efficiency
[edit]
where
- , mechanical pump efficiency percent
- , theoretical torque to drive
- , actual torque to drive
Hydraulic efficiency
[edit]
where
- , hydraulic pump efficiency
- , theoretical flow rate output
- , actual flow rate output
References
[edit]- ^ Parr, Andrew (2011). "Hydraulics and Pneumatics a technician's and engineer's guide", p. 38. Elsevier.
- ^ "4 Design Features That Determine Hydraulic Gear Pump Selection". www.blueascend.com. Retrieved 2023-07-21.
- ^ "Hydraulic Pumps | Hydraulic Parts USA". hydraulicpartsusa.com. Retrieved 2024-05-31.
- ^ "AMPHIMAX HYDRAULICS PUMPS WHEEL MOTORS CONTROLS VALVES". www.bluebird-electric.net. Retrieved 2024-05-31.


















