Koch snowflake

The first four iterations of the Koch snowflake

The first seven iterations in animation

The Koch curve

The Koch snowflake (also known as the Koch star and Koch island) is a mathematical curve and one of the earliest fractal curves to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire) by the Swedish mathematician Helge von Koch.

Construction

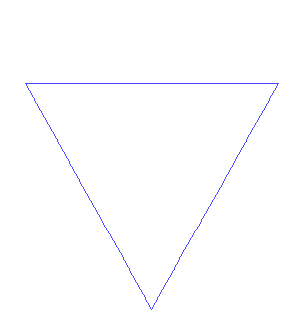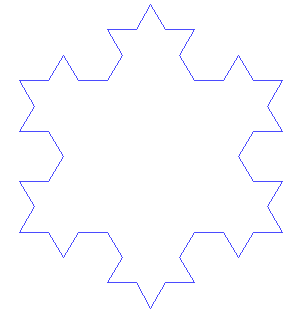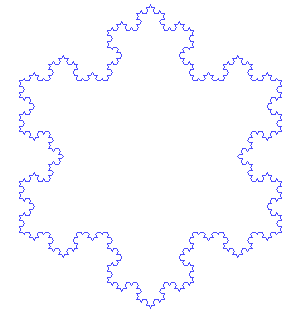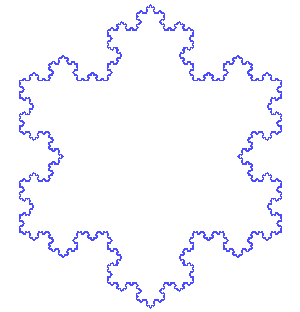
The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows:

1. divide the line segment into three segments of equal length.
2. draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.
3. remove the line segment that is the base of the triangle from step 2.

After one iteration of this process, the resulting shape is the outline of a hexagram.

The Koch snowflake is the limit approached as the above steps are followed over and over again. The Koch curve originally described by Koch is constructed with only one of the three sides of the original triangle. In other words, three Koch curves make a Koch snowflake.

Properties

The Koch curve has an infinite length because each time the steps above are performed on each line segment of the figure there are four times as many line segments, the length of each being one-third the length of the segments in the previous stage. Hence, the total length increases by one third and thus the length at step n will be (4/3)ⁿ of the original triangle perimeter: the fractal dimension is log 4/log 3 ≈ 1.26, greater than the dimension of a line (1) but less than Peano's space-filling curve (2).

The Koch curve is continuous everywhere but differentiable nowhere.

Taking s as the side length, the original triangle area is ${\frac {s^{2}{\sqrt {3}}}{4}}$ . The side length of each successive small triangle is 1/3 of those in the previous iteration; because the area of the added triangles is proportional to the square of its side length, the area of each triangle added in the nth step is 1/9 of that in the (n-1)th step. In each iteration after the first, 4 times as many triangles are added as in the previous iteration; because the first iteration adds 3 triangles then the nth iteration will add $3\cdot 4^{n-1}$ triangles. Combining these two formulae gives the iteration formula:

$A_{n+1}=A_{n}+{\frac {3\cdot 4^{n-1}}{9^{n}}}A_{0}\quad n\geq 1\,,$

where $A_{0}$ is area of the original triangle. Substituting in

$A_{1}={\frac {4}{3}}A_{0}\,,$

and expanding yields:

${\begin{aligned}A_{n+1}&={\frac {4}{3}}A_{0}+\sum _{k=2}^{n}{\frac {3\cdot 4^{k-1}}{9^{k}}}A_{0}=\left({\frac {4}{3}}+{\frac {1}{3}}\sum _{k=2}^{n}3{\frac {3\cdot 4^{k-1}}{9^{k}}}\right)A_{0}\\&=\left({\frac {4}{3}}+{\frac {1}{3}}\sum _{k=2}^{n}{\frac {9\cdot 4^{k-1}}{9^{k}}}\right)A_{0}=\left({\frac {4}{3}}+{\frac {1}{3}}\sum _{k=1}^{n}{\frac {4^{k}}{9^{k}}}\right)A_{0}\,.\end{aligned}}$

In the limit, as n goes to infinity, the limit of the sum of the powers of 4/9 is 4/5, so

$\lim _{n\rightarrow \infty }A_{n}=\left({\frac {4}{3}}+{\frac {1}{3}}\cdot {\frac {4}{5}}\right)A_{0}={\frac {8}{5}}A_{0}\,.$

So the area of a Koch snowflake is 8/5 of the area of the original triangle, or ${\frac {2s^{2}{\sqrt {3}}}{5}}$. Therefore the infinite perimeter of the Koch triangle encloses a finite area.

Tesselation by two sizes of Koch snowflake

It is possible to tessellate the plane by copies of Koch snowflakes in two different sizes. However, such a tessellation is not possible using only snowflakes of the same size as each other. Since each Koch snowflake in the tesselation can be subdivided into seven smaller snowflakes of two different sizes, it is also possible to find tessellations that use more than two sizes at once.

Thue-Morse Sequence and Turtle graphics

A Turtle Graphic is the curve that is generated if an automaton is programmed with a sequence. If the Thue–Morse sequence members are used in order to select program states:

• If t(n) = 0, move ahead by one unit,
• If t(n) = 1, rotate counterclockwise by an angle of π/3,

the resulting curve converges to the Koch snowflake.

Representation as Lindenmayer system

The Koch Curve can be expressed by a rewrite system (Lindenmayer system).

Alphabet : F

Constants : +, −

Axiom : F++F++F

Production rules:

F → F−F++F−F

Here, F means "draw forward", + means "turn right 60°", and − means "turn left 60°".

Variants of the Koch curve

Following von Koch's concept, several variants of the Koch curve were designed, considering right angles (quadratic), other angles (Césaro) or circles and their extensions to higher dimensions (Sphereflake):

Variant	Illustration	Construction
1D, 85° angle	Cesaro fractal	The Cesaro fractal is a variant of the Koch curve with an angle between 60° and 90° (here 85°).
1D, 90° angle	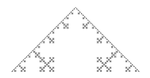Quadratic type 1 curve	The first 2 iterations
1D, 90° angle	Quadratic type 2 curve	The first 2 iterations. Its fractal dimension equals 1.5 and is exactly half-way between dimension 1 and 2. It is therefore often chosen when studying the physical properties of non-integer fractal objects.
1D, ln 3/ln (√5)	Quadratic flake	The first 2 iterations. Its fractal dimension equals ln 3/ln (√5)=1.37.
1D, ln 3.33/ln (√5)	Quadratic Cross	Another variation. Its fractal dimension equals ln 3.33/ln (√5)=1.49.
2D, triangles	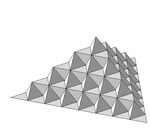von Koch surface	The first 3 iterations of a natural extension of the Koch curve in 2 dimensions
2D, 90° angle	Quadratic type 1 surface	Extension of the quadratic type 1 curve. The illustration at left shows the fractal after the second iteration Animation quadratic surface .
2D, 90° angle	Quadratic type 2 surface	Extension of the quadratic type 2 curve. The illustration at left shows the fractal after the first iteration.
2D, spheres	Closeup of Haines sphereflake	Eric Haines has developed the sphereflake fractal, which is a three-dimensional version of the Koch snowflake, using spheres.

See also

• List of fractals by Hausdorff dimension
• Gabriel's Horn (infinite surface area but encloses a finite volume)
• Flowsnake

References

• Edward Kasner & James Newman, Mathematics and the Imagination Dover Press reprint of Simon & Schuster (1940) ISBN 0-486-41703-4, pp 344–51.

External links

• von Koch Curve
• The Koch snowflake in Mathworld
• Application of the Koch curve to an antenna
• "A mathematical analysis of the Koch curve and quadratic Koch curve" (pdf). Retrieved 22 November 2011.