Left recursion
This article may be too technical for most readers to understand. (November 2015) |
In the formal language theory of computer science, left recursion is a special case of recursion where a string is recognized as part of a language by the fact that it decomposes into a string from that same language (on the left) and a suffix (on the right). For instance, can be recognized as a sum because it can be broken into , also a sum, and , a suitable suffix.
In terms of context-free grammar, a nonterminal is left-recursive if the leftmost symbol in one of its productions is itself (in the case of direct left recursion) or can be made itself by some sequence of substitutions (in the case of indirect left recursion).
Definition[edit]
A grammar is left-recursive if and only if there exists a nonterminal symbol that can derive to a sentential form with itself as the leftmost symbol.[1] Symbolically,
- ,
where indicates the operation of making one or more substitutions, and is any sequence of terminal and nonterminal symbols.
Direct left recursion[edit]
Direct left recursion occurs when the definition can be satisfied with only one substitution. It requires a rule of the form
where is a sequence of nonterminals and terminals . For example, the rule
is directly left-recursive. A left-to-right recursive descent parser for this rule might look like
void Expression() {
Expression();
match('+');
Term();
}
and such code would fall into infinite recursion when executed.
Indirect left recursion[edit]
Indirect left recursion occurs when the definition of left recursion is satisfied via several substitutions. It entails a set of rules following the pattern
where are sequences that can each yield the empty string, while may be any sequences of terminal and nonterminal symbols at all. Note that these sequences may be empty. The derivation
then gives as leftmost in its final sentential form.
Uses[edit]
Left recursion is commonly used as an idiom for making operations left-associative: that an expression a+b-c-d+e is evaluated as (((a+b)-c)-d)+e. In this case, that evaluation order could be achieved as a matter of syntax via the three grammatical rules
These only allow parsing the a+b-c-d+e as consisting of the a+b-c-d and e, where a+b-c-d in turn consists of the a+b-c and d, while a+b-c consists of the a+b and c, etc.
Removing left recursion[edit]
Left recursion often poses problems for parsers, either because it leads them into infinite recursion (as in the case of most top-down parsers) or because they expect rules in a normal form that forbids it (as in the case of many bottom-up parsers[clarification needed]). Therefore, a grammar is often preprocessed to eliminate the left recursion.
Removing direct left recursion[edit]
The general algorithm to remove direct left recursion follows. Several improvements to this method have been made.[2] For a left-recursive nonterminal , discard any rules of the form and consider those that remain:
where:
- each is a nonempty sequence of nonterminals and terminals, and
- each is a sequence of nonterminals and terminals that does not start with .
Replace these with two sets of productions, one set for :
and another set for the fresh nonterminal (often called the "tail" or the "rest"):
Repeat this process until no direct left recursion remains.
As an example, consider the rule set
This could be rewritten to avoid left recursion as
Removing all left recursion[edit]
The above process can be extended to eliminate all left recursion, by first converting indirect left recursion to direct left recursion on the highest numbered nonterminal in a cycle.
- Inputs A grammar: a set of nonterminals and their productions
- Output A modified grammar generating the same language but without left recursion
- For each nonterminal :
- Repeat until an iteration leaves the grammar unchanged:
- For each rule , being a sequence of terminals and nonterminals:
- If begins with a nonterminal and :
- Let be without its leading .
- Remove the rule .
- For each rule :
- Add the rule .
- If begins with a nonterminal and :
- For each rule , being a sequence of terminals and nonterminals:
- Remove direct left recursion for as described above.
- Repeat until an iteration leaves the grammar unchanged:
- For each nonterminal :
Step 1.1.1 amounts to expanding the initial nonterminal in the right hand side of some rule , but only if . If was one step in a cycle of productions giving rise to a left recursion, then this has shortened that cycle by one step, but often at the price of increasing the number of rules.
The algorithm may be viewed as establishing a topological ordering on nonterminals: afterwards there can only be a rule if . Note that this algorithm is highly sensitive to the nonterminal ordering; optimizations often focus on choosing this ordering well.
Pitfalls[edit]
Although the above transformations preserve the language generated by a grammar, they may change the parse trees that witness strings' recognition. With suitable bookkeeping, tree rewriting can recover the originals, but if this step is omitted, the differences may change the semantics of a parse.
Associativity is particularly vulnerable; left-associative operators typically appear in right-associative-like arrangements under the new grammar. For example, starting with this grammar:
the standard transformations to remove left recursion yield the following:
Parsing the string "1 - 2 - 3" with the first grammar in an LALR parser (which can handle left-recursive grammars) would have resulted in the parse tree:
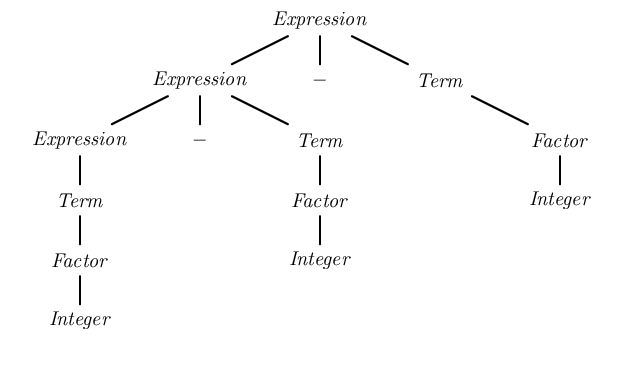
This parse tree groups the terms on the left, giving the correct semantics (1 - 2) - 3.
Parsing with the second grammar gives

which, properly interpreted, signifies 1 + (-2 + (-3)), also correct, but less faithful to the input and much harder to implement for some operators. Notice how terms to the right appear deeper in the tree, much as a right-recursive grammar would arrange them for 1 - (2 - 3).
Accommodating left recursion in top-down parsing[edit]
A formal grammar that contains left recursion cannot be parsed by a LL(k)-parser or other naive recursive descent parser unless it is converted to a weakly equivalent right-recursive form. In contrast, left recursion is preferred for LALR parsers because it results in lower stack usage than right recursion. However, more sophisticated top-down parsers can implement general context-free grammars by use of curtailment. In 2006, Frost and Hafiz described an algorithm which accommodates ambiguous grammars with direct left-recursive production rules.[3] That algorithm was extended to a complete parsing algorithm to accommodate indirect as well as direct left recursion in polynomial time, and to generate compact polynomial-size representations of the potentially exponential number of parse trees for highly ambiguous grammars by Frost, Hafiz and Callaghan in 2007.[4] The authors then implemented the algorithm as a set of parser combinators written in the Haskell programming language.[5]
See also[edit]
References[edit]
- ^ Notes on Formal Language Theory and Parsing at the Wayback Machine (archived 2007-11-27). James Power, Department of Computer Science National University of Ireland, Maynooth Maynooth, Co. Kildare, Ireland.JPR02
- ^ Moore, Robert C. (May 2000). "Removing Left Recursion from Context-Free Grammars" (PDF). 6th Applied Natural Language Processing Conference: 249–255.
- ^ Frost, R.; R. Hafiz (2006). "A New Top-Down Parsing Algorithm to Accommodate Ambiguity and Left Recursion in Polynomial Time". ACM SIGPLAN Notices. 41 (5): 46–54. doi:10.1145/1149982.1149988. S2CID 8006549., available from the author at http://hafiz.myweb.cs.uwindsor.ca/pub/p46-frost.pdf Archived 2015-01-08 at the Wayback Machine
- ^ Frost, R.; R. Hafiz; P. Callaghan (June 2007). "Modular and Efficient Top-Down Parsing for Ambiguous Left-Recursive Grammars" (PDF). 10th International Workshop on Parsing Technologies (IWPT), ACL-SIGPARSE: 109–120. Archived from the original (PDF) on 2011-05-27.
- ^ Frost, R.; R. Hafiz; P. Callaghan (January 2008). "Parser Combinators for Ambiguous Left-Recursive Grammars". Practical Aspects of Declarative Languages (PDF). Lecture Notes in Computer Science. Vol. 4902. pp. 167–181. doi:10.1007/978-3-540-77442-6_12. ISBN 978-3-540-77441-9.
















































