Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines,[1][2] or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects.
Rewriting can be non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several theorem provers[3] and declarative programming languages are based on term rewriting.[4][5]
Example cases[edit]
Logic[edit]
In logic, the procedure for obtaining the conjunctive normal form (CNF) of a formula can be implemented as a rewriting system.[6] The rules of an example of such a system would be:
where the symbol () indicates that an expression matching the left hand side of the rule can be rewritten to one formed by the right hand side, and the symbols each denote a subexpression. In such a system, each rule is chosen so that the left side is equivalent to the right side, and consequently when the left side matches a subexpression, performing a rewrite of that subexpression from left to right maintains logical consistency and value of the entire expression.
Arithmetic[edit]
Term rewriting systems can be employed to compute arithmetic operations on natural numbers. To this end, each such number has to be encoded as a term. The simplest encoding is the one used in the Peano axioms, based on the constant 0 (zero) and the successor function S. For example, the numbers 0, 1, 2, and 3 are represented by the terms 0, S(0), S(S(0)), and S(S(S(0))), respectively. The following term rewriting system can then be used to compute sum and product of given natural numbers.[7]
For example, the computation of 2+2 to result in 4 can be duplicated by term rewriting as follows:
where the rule numbers are given above the rewrites-to arrow.
As another example, the computation of 2⋅2 looks like:
where the last step comprises the previous example computation.
Linguistics[edit]
In linguistics, phrase structure rules, also called rewrite rules, are used in some systems of generative grammar,[8] as a means of generating the grammatically correct sentences of a language. Such a rule typically takes the form , where A is a syntactic category label, such as noun phrase or sentence, and X is a sequence of such labels or morphemes, expressing the fact that A can be replaced by X in generating the constituent structure of a sentence. For example, the rule means that a sentence can consist of a noun phrase (NP) followed by a verb phrase (VP); further rules will specify what sub-constituents a noun phrase and a verb phrase can consist of, and so on.
Abstract rewriting systems[edit]
From the above examples, it is clear that we can think of rewriting systems in an abstract manner. We need to specify a set of objects and the rules that can be applied to transform them. The most general (unidimensional) setting of this notion is called an abstract reduction system[9] or abstract rewriting system (abbreviated ARS).[10] An ARS is simply a set A of objects, together with a binary relation → on A called the reduction relation, rewrite relation[11] or just reduction.[9]
Many notions and notations can be defined in the general setting of an ARS. is the reflexive transitive closure of . is the symmetric closure of . is the reflexive transitive symmetric closure of . The word problem for an ARS is determining, given x and y, whether . An object x in A is called reducible if there exists some other y in A such that ; otherwise it is called irreducible or a normal form. An object y is called a "normal form of x" if , and y is irreducible. If the normal form of x is unique, then this is usually denoted with . If every object has at least one normal form, the ARS is called normalizing. or x and y are said to be joinable if there exists some z with the property that . An ARS is said to possess the Church–Rosser property if implies . An ARS is confluent if for all w, x, and y in A, implies . An ARS is locally confluent if and only if for all w, x, and y in A, implies . An ARS is said to be terminating or noetherian if there is no infinite chain . A confluent and terminating ARS is called convergent or canonical.
Important theorems for abstract rewriting systems are that an ARS is confluent iff it has the Church–Rosser property, Newman's lemma (a terminating ARS is confluent if and only if it is locally confluent), and that the word problem for an ARS is undecidable in general.
String rewriting systems[edit]
A string rewriting system (SRS), also known as semi-Thue system, exploits the free monoid structure of the strings (words) over an alphabet to extend a rewriting relation, , to all strings in the alphabet that contain left- and respectively right-hand sides of some rules as substrings. Formally a semi-Thue system is a tuple where is a (usually finite) alphabet, and is a binary relation between some (fixed) strings in the alphabet, called the set of rewrite rules. The one-step rewriting relation induced by on is defined as: if are any strings, then if there exist such that , , and . Since is a relation on , the pair fits the definition of an abstract rewriting system. Since the empty string is in , is a subset of . If the relation is symmetric, then the system is called a Thue system.
In a SRS, the reduction relation is compatible with the monoid operation, meaning that implies for all strings . Similarly, the reflexive transitive symmetric closure of , denoted , is a congruence, meaning it is an equivalence relation (by definition) and it is also compatible with string concatenation. The relation is called the Thue congruence generated by . In a Thue system, i.e. if is symmetric, the rewrite relation coincides with the Thue congruence .
The notion of a semi-Thue system essentially coincides with the presentation of a monoid. Since is a congruence, we can define the factor monoid of the free monoid by the Thue congruence. If a monoid is isomorphic with , then the semi-Thue system is called a monoid presentation of .
We immediately get some very useful connections with other areas of algebra. For example, the alphabet with the rules , where is the empty string, is a presentation of the free group on one generator. If instead the rules are just , then we obtain a presentation of the bicyclic monoid. Thus semi-Thue systems constitute a natural framework for solving the word problem for monoids and groups. In fact, every monoid has a presentation of the form , i.e. it may always be presented by a semi-Thue system, possibly over an infinite alphabet.
The word problem for a semi-Thue system is undecidable in general; this result is sometimes known as the Post–Markov theorem.[12]
Term rewriting systems[edit]

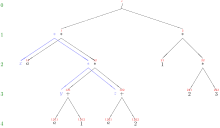
A term rewriting system (TRS) is a rewriting system whose objects are terms, which are expressions with nested sub-expressions. For example, the system shown under § Logic above is a term rewriting system. The terms in this system are composed of binary operators and and the unary operator . Also present in the rules are variables, which represent any possible term (though a single variable always represents the same term throughout a single rule).
In contrast to string rewriting systems, whose objects are sequences of symbols, the objects of a term rewriting system form a term algebra. A term can be visualized as a tree of symbols, the set of admitted symbols being fixed by a given signature. As a formalism, term rewriting systems have the full power of Turing machines, that is, every computable function can be defined by a term rewriting system.[13]
Formal definition [edit]
A rewrite rule is a pair of terms, commonly written as , to indicate that the left-hand side l can be replaced by the right-hand side r. A term rewriting system is a set R of such rules. A rule can be applied to a term s if the left term l matches some subterm of s, that is, if there is some substitution such that the subterm of rooted at some position p is the result of applying the substitution to the term l. The subterm matching the left hand side of the rule is called a redex or reducible expression.[14] The result term t of this rule application is then the result of replacing the subterm at position p in s by the term with the substitution applied, see picture 1. In this case, is said to be rewritten in one step, or rewritten directly, to by the system , formally denoted as , , or as by some authors.
If a term can be rewritten in several steps into a term , that is, if , the term is said to be rewritten to , formally denoted as . In other words, the relation is the transitive closure of the relation ; often, also the notation is used to denote the reflexive-transitive closure of , that is, if or .[15] A term rewriting given by a set of rules can be viewed as an abstract rewriting system as defined above, with terms as its objects and as its rewrite relation.
For example, is a rewrite rule, commonly used to establish a normal form with respect to the associativity of . That rule can be applied at the numerator in the term with the matching substitution , see picture 2.[note 2] Applying that substitution to the rule's right-hand side yields the term , and replacing the numerator by that term yields , which is the result term of applying the rewrite rule. Altogether, applying the rewrite rule has achieved what is called "applying the associativity law for to " in elementary algebra. Alternately, the rule could have been applied to the denominator of the original term, yielding .
Termination[edit]
Termination issues of rewrite systems in general are handled in Abstract rewriting system#Termination and convergence. For term rewriting systems in particular, the following additional subtleties are to be considered.
Termination even of a system consisting of one rule with a linear left-hand side is undecidable.[16][17] Termination is also undecidable for systems using only unary function symbols; however, it is decidable for finite ground systems.[18]
The following term rewrite system is normalizing,[note 3] but not terminating,[note 4] and not confluent:[19]
The following two examples of terminating term rewrite systems are due to Toyama:[20]
and
Their union is a non-terminating system, since
See Rewrite order and Path ordering (term rewriting) for ordering relations used in termination proofs for term rewriting systems.
Higher-order rewriting systems[edit]
Higher-order rewriting systems are a generalization of first-order term rewriting systems to lambda terms, allowing higher order functions and bound variables.[22] Various results about first-order TRSs can be reformulated for HRSs as well.[23]
Graph rewriting systems[edit]
Graph rewrite systems are another generalization of term rewrite systems, operating on graphs instead of (ground-) terms / their corresponding tree representation.
Trace rewriting systems[edit]
Trace theory provides a means for discussing multiprocessing in more formal terms, such as via the trace monoid and the history monoid. Rewriting can be performed in trace systems as well.
See also[edit]
- Critical pair (logic)
- Compiler
- Knuth–Bendix completion algorithm
- L-systems specify rewriting that is done in parallel.
- Referential transparency in computer science
- Regulated rewriting
- Rho calculus
- Interaction Nets
Notes[edit]
- ^ This variant of the previous rule is needed since the commutative law A∨B = B∨A cannot be turned into a rewrite rule. A rule like A∨B → B∨A would cause the rewrite system to be nonterminating.
- ^ since applying that substitution to the rule's left hand side yields the numerator
- ^ i.e. for each term, some normal form exists, e.g. h(c,c) has the normal forms b and g(b), since h(c,c) → f(h(c,c),h(c,c)) → f(h(c,c),f(h(c,c),h(c,c))) → f(h(c,c),g(h(c,c))) → b, and h(c,c) → f(h(c,c),h(c,c)) → g(h(c,c)) → ... → g(b); neither b nor g(b) can be rewritten any further, therefore the system is not confluent
- ^ i.e., there are infinite derivations, e.g. h(c,c) → f(h(c,c),h(c,c)) → f(f(h(c,c),h(c,c)) ,h(c,c)) → f(f(f(h(c,c),h(c,c)),h(c,c)) ,h(c,c)) → ...
Further reading[edit]
- Baader, Franz; Nipkow, Tobias (1999). Term rewriting and all that. Cambridge University Press. ISBN 978-0-521-77920-3. 316 pages.
- Marc Bezem, Jan Willem Klop, Roel de Vrijer ("Terese"), Term Rewriting Systems ("TeReSe"), Cambridge University Press, 2003, ISBN 0-521-39115-6. This is the most recent comprehensive monograph. It uses however a fair deal of non-yet-standard notations and definitions. For instance, the Church–Rosser property is defined to be identical with confluence.
- Nachum Dershowitz and Jean-Pierre Jouannaud "Rewrite Systems", Chapter 6 in Jan van Leeuwen (Ed.), Handbook of Theoretical Computer Science, Volume B: Formal Models and Semantics., Elsevier and MIT Press, 1990, ISBN 0-444-88074-7, pp. 243–320. The preprint of this chapter is freely available from the authors, but it is missing the figures.
- Nachum Dershowitz and David Plaisted. "Rewriting", Chapter 9 in John Alan Robinson and Andrei Voronkov (Eds.), Handbook of Automated Reasoning, Volume 1.
- Gérard Huet et Derek Oppen, Equations and Rewrite Rules, A Survey (1980) Stanford Verification Group, Report N° 15 Computer Science Department Report N° STAN-CS-80-785
- Jan Willem Klop. "Term Rewriting Systems", Chapter 1 in Samson Abramsky, Dov M. Gabbay and Tom Maibaum (Eds.), Handbook of Logic in Computer Science, Volume 2: Background: Computational Structures.
- David Plaisted. "Equational reasoning and term rewriting systems", in Dov M. Gabbay, C. J. Hogger and John Alan Robinson (Eds.), Handbook of Logic in Artificial Intelligence and Logic Programming, Volume 1.
- Jürgen Avenhaus and Klaus Madlener. "Term rewriting and equational reasoning". In Ranan B. Banerji (Ed.), Formal Techniques in Artificial Intelligence: A Sourcebook, Elsevier (1990).
- String rewriting
- Ronald V. Book and Friedrich Otto, String-Rewriting Systems, Springer (1993).
- Benjamin Benninghofen, Susanne Kemmerich and Michael M. Richter, Systems of Reductions. LNCS 277, Springer-Verlag (1987).
- Other
- Martin Davis, Ron Sigal, Elaine J. Weyuker, (1994) Computability, Complexity, and Languages: Fundamentals of Theoretical Computer Science – 2nd edition, Academic Press, ISBN 0-12-206382-1.
External links[edit]
- The Rewriting Home Page
- IFIP Working Group 1.6
- Researchers in rewriting by Aart Middeldorp, University of Innsbruck
- Termination Portal
- Maude System — a software implementation of a generic term rewriting system.[5]
References[edit]
- ^ Joseph Goguen "Proving and Rewriting" International Conference on Algebraic and Logic Programming, 1990 Nancy, France pp 1-24
- ^ Sculthorpe, Neil; Frisby, Nicolas; Gill, Andy (2014). "The Kansas University rewrite engine" (PDF). Journal of Functional Programming. 24 (4): 434–473. doi:10.1017/S0956796814000185. ISSN 0956-7968. S2CID 16807490. Archived (PDF) from the original on 2017-09-22. Retrieved 2019-02-12.
- ^ Hsiang, Jieh; Kirchner, Hélène; Lescanne, Pierre; Rusinowitch, Michaël (1992). "The term rewriting approach to automated theorem proving". The Journal of Logic Programming. 14 (1–2): 71–99. doi:10.1016/0743-1066(92)90047-7.
- ^ Frühwirth, Thom (1998). "Theory and practice of constraint handling rules". The Journal of Logic Programming. 37 (1–3): 95–138. doi:10.1016/S0743-1066(98)10005-5.
- ^ a b Clavel, M.; Durán, F.; Eker, S.; Lincoln, P.; Martí-Oliet, N.; Meseguer, J.; Quesada, J.F. (2002). "Maude: Specification and programming in rewriting logic". Theoretical Computer Science. 285 (2): 187–243. doi:10.1016/S0304-3975(01)00359-0.
- ^ Kim Marriott; Peter J. Stuckey (1998). Programming with Constraints: An Introduction. MIT Press. pp. 436–. ISBN 978-0-262-13341-8.
- ^ Jürgen Avenhaus; Klaus Madlener (1990). "Term Rewriting and Equational Reasoning". In R.B. Banerji (ed.). Formal Techniques in Artificial Intelligence. Sourcebook. Elsevier. pp. 1–43. Here: Example in sect.4.1, p.24.
- ^ Robert Freidin (1992). Foundations of Generative Syntax. MIT Press. ISBN 978-0-262-06144-5.
- ^ a b Book and Otto, p. 10
- ^ Bezem et al., p. 7,
- ^ Bezem et al., p. 7
- ^ Martin Davis et al. 1994, p. 178
- ^ Dershowitz, Jouannaud (1990), sect.1, p.245
- ^ Klop, J. W. "Term Rewriting Systems" (PDF). Papers by Nachum Dershowitz and students. Tel Aviv University. p. 12. Archived (PDF) from the original on 15 August 2021. Retrieved 14 August 2021.
- ^ N. Dershowitz, J.-P. Jouannaud (1990). Jan van Leeuwen (ed.). Rewrite Systems. Handbook of Theoretical Computer Science. Vol. B. Elsevier. pp. 243–320.; here: Sect. 2.3
- ^ Max Dauchet (1989). "Simulation of Turing Machines by a Left-Linear Rewrite Rule". Proc. 3rd Int. Conf. on Rewriting Techniques and Applications. LNCS. Vol. 355. Springer. pp. 109–120.
- ^ Max Dauchet (Sep 1992). "Simulation of Turing machines by a regular rewrite rule". Theoretical Computer Science. 103 (2): 409–420. doi:10.1016/0304-3975(92)90022-8.
- ^ Gerard Huet, D.S. Lankford (Mar 1978). On the Uniform Halting Problem for Term Rewriting Systems (PDF) (Technical report). IRIA. p. 8. 283. Retrieved 16 June 2013.
- ^ Bernhard Gramlich (Jun 1993). "Relating Innermost, Weak, Uniform, and Modular Termination of Term Rewriting Systems". In Voronkov, Andrei (ed.). Proc. International Conference on Logic Programming and Automated Reasoning (LPAR). LNAI. Vol. 624. Springer. pp. 285–296. Archived from the original on 2016-03-04. Retrieved 2014-06-19. Here: Example 3.3
- ^ Yoshihito Toyama (1987). "Counterexamples to Termination for the Direct Sum of Term Rewriting Systems" (PDF). Inf. Process. Lett. 25 (3): 141–143. doi:10.1016/0020-0190(87)90122-0. hdl:2433/99946. Archived (PDF) from the original on 2019-11-13. Retrieved 2019-11-13.
- ^ N. Dershowitz (1985). "Termination" (PDF). In Jean-Pierre Jouannaud (ed.). Proc. RTA. LNCS. Vol. 220. Springer. pp. 180–224. Archived (PDF) from the original on 2013-11-12. Retrieved 2013-06-16.; here: p.210
- ^ Wolfram, D. A. (1993). The Clausal Theory of Types. Cambridge University Press. pp. 47–50. doi:10.1017/CBO9780511569906. ISBN 9780521395380. S2CID 42331173.
- ^ Nipkow, Tobias; Prehofer, Christian (1998). "Higher-Order Rewriting and Equational Reasoning". In Bibel, W.; Schmitt, P. (eds.). Automated Deduction - A Basis for Applications. Volume I: Foundations. Kluwer. pp. 399–430. Archived from the original on 2021-08-16. Retrieved 2021-08-16.































































































