Lorentz factor

The Lorentz factor or Lorentz term is an expression which appears in several equations in special relativity. It arises from deriving the Lorentz transformations. The name originates from its earlier appearance in Lorentzian electrodynamics - named after the Dutch physicist Hendrik Lorentz.

Due to its ubiquity, physicists generally represent it with the symbol γ (Greek lowercase gamma). Sometimes (especially in discussion of superluminal motion) the factor is written as Γ (Greek uppercase-gamma) rather than γ (lowercase-gamma).

Definition

The Lorentz factor is defined as:

$\gamma = \frac{1}{\sqrt{1 - v^2/c^2}} = \frac{1}{\sqrt{1 - \beta^2}} = \frac{\mathrm{d}t}{\mathrm{d}\tau}$

where:

• v is the relative velocity between inertial reference frames,
• β is the ratio of v to the speed of light c.
• τ is the proper time for an observer (measuring time intervals in the observer's own frame),
• c is the speed of light.

This is the most frequently used form in practice, though not the only one (see below for alternative forms).

Occurrence

Following is a list of formulae from Special relativity which use γ as a shorthand:

• The Lorentz transformation: The simplest case is a boost in the x-direction (more general forms including arbitrary directions and rotations not listed here), which describes how spacetime coordinates change from one inertial frame using coordinates (x, y, z, t) to another (x ', y ', z ', t ') with relative velocity v:

$t' = \gamma \left( t - \frac{vx}{c^2} \right )$

$x' = \gamma \left( x - vt \right )$

Corollaries of the above transformations are the results:

• Time dilation: The time (∆t') between two ticks as measured in the frame in which the clock is moving, is longer than the time (∆t) between these ticks as measured in the rest frame of the clock:

$\Delta t' = \gamma \Delta t. \,$

• Length contraction: The length (∆x') of an object as measured in the frame in which it is moving, is shorter than its length (∆x) in its own rest frame:

$\Delta x' = \Delta x/\gamma. \,\!$

Applying conservation of momentum and energy leads to these results:

• Relativistic mass:' The mass of an object m in motion is dependent on γ and the rest mass m₀:

$m = \gamma m_0. \,$

• Relativistic momentum: The relativistic momentum relation takes the same form as for classical momentum, but using the above relativistic mass:

$\vec p = m \vec v = \gamma m_0 \vec v. \,$

Numerical values

Lorentz factor γ as a function of velocity. Its initial value is 1 (when v = 0); and as velocity approaches the speed of light (v → c) γ increases without bound (γ → ∞).

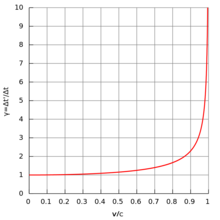
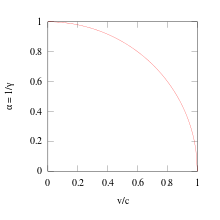
In the chart below, the left-hand column shows speeds as different fractions of the speed of light (i.e. in units of c). The middle column shows the corresponding Lorentz factor, the final is the reciprocal.

Speed (units of c)	Lorentz factor	Reciprocal
$\beta = v/c \,\!$	$\gamma \,\!$	$1/\gamma \,\!$
0.000	1.000	1.000
0.100	1.005	0.995
0.200	1.021	0.980
0.300	1.048	0.954
0.400	1.091	0.917
0.500	1.155	0.866
0.600	1.250	0.800
0.700	1.400	0.714
0.800	1.667	0.600
0.866	2.000	0.500
0.900	2.294	0.436
0.990	7.089	0.141
0.999	22.366	0.045

Alternative representations

Main articles: Momentum and Rapidity

Naturally there are other ways to write the factor. Above, velocity v was used, but related variables such as momentum and rapidity may also be convenient.

Momentum

Solving the previous relativistic momentum equation for γ leads to:

$\gamma = \sqrt{1+\left ( \frac{p}{m_0 c} \right )^2 }$

This form is rarely used, it does however appear in the Maxwell–Juttner distribution.

Rapidity

Applying the definition of rapidity as the following hyperbolic angle φ:

$\tanh \varphi = \beta \,\!$

also leads to γ (by use of hyperbolic identities):

$\gamma = \cosh \varphi = \frac{1}{\sqrt{1 - \tanh^2 \varphi}} = \frac{1}{\sqrt{1 - \beta^2}} \,\!$

Using the property of Lorentz transformation, it can be shown that rapidity is additive, a useful property that velocity does not have. Thus the rapidity parameter forms a one-parameter group, a foundation for physical models.

Series expansion (velocity)

The Lorentz factor has a Maclaurin series of:

$\gamma ( \beta ) = 1 + \frac{1}{2} \beta^2 + \frac{3}{8} \beta^4 + \frac{5}{16} \beta^6 + \frac{35}{128} \beta^8 + ...$

The approximation γ ≈ 1 + ¹/₂ β² may be used to calculate relativistic effects at low speeds. It holds to within 1% error for v < 0.4 c (v < 120,000 km/s), and to within 0.1% error for v < 0.22 c (v < 66,000 km/s).

The truncated versions of this series also allow physicists to prove that special relativity reduces to Newtonian mechanics at low speeds. For example, in special relativity, the following two equations hold:

$\vec p = \gamma m \vec v$

$E = \gamma m c^2 \,$

For γ ≈ 1 and γ ≈ 1 + ¹/₂ β², respectively, these reduce to their Newtonian equivalents:

$\vec p = m \vec v$

$E = m c^2 + \frac{1}{2} m v^2$

The Lorentz factor equation can also be inverted to yield:

$\beta = \sqrt{1 - \frac{1}{\gamma^2}}$

This has an asymptotic form of:

$\beta = 1 - \frac{1}{2} \gamma^{-2} - \frac{1}{8} \gamma^{-4} - \frac{1}{16} \gamma^{-6} - \frac{5}{128} \gamma^{-8} + ...$

The first two terms are occasionally used to quickly calculate velocities from large γ values. The approximation β ≈ 1 - ¹/₂ γ⁻² holds to within 1% tolerance for γ > 2, and to within 0.1% tolerance for γ > 3.5.

See also

• Special relativity
• Inertial frame of reference
• Lorentz transformation
• Pseudorapidity
• Proper velocity