Oversampled binary image sensor
An oversampled binary image sensor is an image sensor with non-linear response capabilities reminiscent of traditional photographic film.[1][2] Each pixel in the sensor has a binary response, giving only a one-bit quantized measurement of the local light intensity. The response function of the image sensor is non-linear and similar to a logarithmic function, which makes the sensor suitable for high dynamic range imaging.[1]
Working principle[edit]
Before the advent of digital image sensors, photography, for the most part of its history, used film to record light information. At the heart of every photographic film are a large number of light-sensitive grains of silver-halide crystals.[3] During exposure, each micron-sized grain has a binary fate: Either it is struck by some incident photons and becomes "exposed", or it is missed by the photon bombardment and remains "unexposed". In the subsequent film development process, exposed grains, due to their altered chemical properties, are converted to silver metal, contributing to opaque spots on the film; unexposed grains are washed away in a chemical bath, leaving behind the transparent regions on the film. Thus, in essence, photographic film is a binary imaging medium, using local densities of opaque silver grains to encode the original light intensity information. Thanks to the small size and large number of these grains, one hardly notices this quantized nature of film when viewing it at a distance, observing only a continuous gray tone.
The oversampled binary image sensor is reminiscent of photographic film. Each pixel in the sensor has a binary response, giving only a one-bit quantized measurement of the local light intensity. At the start of the exposure period, all pixels are set to 0. A pixel is then set to 1 if the number of photons reaching it during the exposure is at least equal to a given threshold q. One way to build such binary sensors is to modify standard memory chip technology, where each memory bit cell is designed to be sensitive to visible light.[4] With current CMOS technology, the level of integration of such systems can exceed 109~1010 (i.e., 1 giga to 10 giga) pixels per chip. In this case, the corresponding pixel sizes (around 50~nm [5]) are far below the diffraction limit of light, and thus the image sensor is oversampling the optical resolution of the light field. Intuitively, one can exploit this spatial redundancy to compensate for the information loss due to one-bit quantizations, as is classic in oversampling delta-sigma converters.[6]
Building a binary sensor that emulates the photographic film process was first envisioned by Fossum,[7] who coined the name digital film sensor (now referred to as a quanta image sensor[8]). The original motivation was mainly out of technical necessity. The miniaturization of camera systems calls for the continuous shrinking of pixel sizes. At a certain point, however, the limited full-well capacity (i.e., the maximum photon-electrons a pixel can hold) of small pixels becomes a bottleneck, yielding very low signal-to-noise ratios (SNRs) and poor dynamic ranges. In contrast, a binary sensor whose pixels need to detect only a few photon-electrons around a small threshold q has much less requirement for full-well capacities, allowing pixel sizes to shrink further.
Imaging model[edit]
Lens[edit]

Consider a simplified camera model shown in Fig.1. The is the incoming light intensity field. By assuming that light intensities remain constant within a short exposure period, the field can be modeled as only a function of the spatial variable . After passing through the optical system, the original light field gets filtered by the lens, which acts like a linear system with a given impulse response. Due to imperfections (e.g., aberrations) in the lens, the impulse response, a.k.a. the point spread function (PSF) of the optical system, cannot be a Dirac delta, thus, imposing a limit on the resolution of the observable light field. However, a more fundamental physical limit is due to light diffraction.[9] As a result, even if the lens is ideal, the PSF is still unavoidably a small blurry spot. In optics, such diffraction-limited spot is often called the Airy disk,[9] whose radius can be computed as
where is the wavelength of the light and is the F-number of the optical system. Due to the lowpass (smoothing) nature of the PSF, the resulting has a finite spatial-resolution, i.e., it has a finite number of degrees of freedom per unit space.
Sensor[edit]
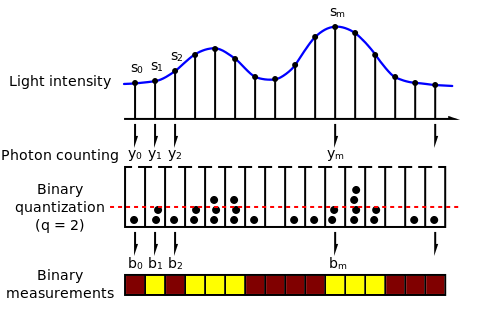
Fig.2 illustrates the binary sensor model. The denote the exposure values accumulated by the sensor pixels. Depending on the local values of , each pixel (depicted as "buckets" in the figure) collects a different number of photons hitting on its surface. is the number of photons impinging on the surface of the th pixel during an exposure period. The relation between and the photon count is stochastic. More specifically, can be modeled as realizations of a Poisson random variable, whose intensity parameter is equal to ,
As a photosensitive device, each pixel in the image sensor converts photons to electrical signals, whose amplitude is proportional to the number of photons impinging on that pixel. In a conventional sensor design, the analog electrical signals are then quantized by an A/D converter into 8 to 14 bits (usually the more bits the better). But in the binary sensor, the quantizer is 1 bit. In Fig.2, is the quantized output of the th pixel. Since the photon counts are drawn from random variables, so are the binary sensor output .
Spatial and temporal oversampling[edit]
If it is allowed to have temporal oversampling, i.e., taking multiple consecutive and independent frames without changing the total exposure time , the performance of the binary sensor is equivalent to the sensor with same number of spatial oversampling under certain condition.[2] It means that people can make trade off between spatial oversampling and temporal oversampling. This is quite important, since technology usually gives limitation on the size of the pixels and the exposure time.
Advantages over traditional sensors[edit]
Due to the limited full-well capacity of conventional image pixel, the pixel will saturate when the light intensity is too strong. This is the reason that the dynamic range of the pixel is low. For the oversampled binary image sensor, the dynamic range is not defined for a single pixel, but a group of pixels, which makes the dynamic range high.[2]
Reconstruction[edit]

One of the most important challenges with the use of an oversampled binary image sensor is the reconstruction of the light intensity from the binary measurement . Maximum likelihood estimation can be used for solving this problem.[2] Fig. 4 shows the results of reconstructing the light intensity from 4096 binary images taken by single photon avalanche diodes (SPADs) camera.[10] A better reconstruction quality with fewer temporal measurements and faster, hardware friendly implementation, can be achieved by more sophisticated algorithms.[11]
References[edit]
- ^ a b L. Sbaiz, F. Yang, E. Charbon, S. Süsstrunk and M. Vetterli, The Gigavision Camera, Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1093 - 1096, 2009.
- ^ a b c d F. Yang, Y.M. Lu, L. Saibz and M. Vetterli, Bits from Photons: Oversampled Image Acquisition Using Binary Poisson Statistics, IEEE Transactions on Image Processing, vol. 21, issue 4, pp.1421-1436, 2012.
- ^ T. H. James, The Theory of The Photographic Process, 4th ed., New York: Macmillan Publishing Co., Inc., 1977.
- ^ S. A. Ciarcia, A 64K-bit dynamic RAM chip is the visual sensor in this digital image camera, Byte Magazine, pp.21-31, Sep. 1983.
- ^ Y. K. Park, S. H. Lee, J. W. Lee et al., Fully integrated 56nm DRAM technology for 1Gb DRAM, in IEEE Symposium on VLSI Technology, Kyoto, Japan, Jun. 2007.
- ^ J. C. Candy and G. C. Temes, Oversamling Delta-Sigma Data Converters-Theory, Design and Simulation. New York, NY: IEEE Press, 1992.
- ^ E. R. Fossum, What to do with sub-diffraction-limit (SDL) pixels? - A proposal for a gigapixel digital film sensor (DFS), in IEEE Workshop on Charge-Coupled Devices and Advanced Image Sensors, Nagano, Japan, Jun. 2005, pp.214-217.
- ^ E.R. Fossum, J. Ma, S. Masoodian, L. Anzagira, and R. Zizza, The quanta image sensor: every photon counts, MDPI Sensors, vol. 16, no. 8, 1260; August 2016. doi:10.3390/s16081260 (Special Issue on Photon-Counting Image Sensors)
- ^ a b M. Born and E. Wolf, Principles of Optics, 7th ed. Cambridge: Cambridge University Press, 1999
- ^ a b L. Carrara, C. Niclass, N. Scheidegger, H. Shea, and E. Charbon, A gamma, X-ray and high energy proton radiation-tolerant CMOS image sensor for space applications, in IEEE International Solid-State Circuits Conference, Feb. 2009, pp.40-41.
- ^ Litany, Or; Remez, Tal; Bronstein, Alex (2015-12-06). "Image reconstruction from dense binary pixels". Signal Processing with Adaptive Sparse Structured Representations (SPARS 2015). arXiv:1512.01774. Bibcode:2015arXiv151201774L.














