Rydberg atom

A Rydberg atom is an excited atom with one or more electrons that have a very high principal quantum number, n.[1][2] The higher the value of n, the farther the electron is from the nucleus, on average. Rydberg atoms have a number of peculiar properties including an exaggerated response to electric and magnetic fields,[3] long decay periods and electron wavefunctions that approximate, under some conditions, classical orbits of electrons about the nuclei.[4] The core electrons shield the outer electron from the electric field of the nucleus such that, from a distance, the electric potential looks identical to that experienced by the electron in a hydrogen atom.[5]
In spite of its shortcomings, the Bohr model of the atom is useful in explaining these properties. Classically, an electron in a circular orbit of radius r, about a hydrogen nucleus of charge +e, obeys Newton's second law:
where k = 1/(4πε0).
Orbital momentum is quantized in units of ħ:
- .
Combining these two equations leads to Bohr's expression for the orbital radius in terms of the principal quantum number, n:
It is now apparent why Rydberg atoms have such peculiar properties: the radius of the orbit scales as n2 (the n = 137 state of hydrogen has an atomic radius ~1 µm) and the geometric cross-section as n4. Thus, Rydberg atoms are extremely large, with loosely bound valence electrons, easily perturbed or ionized by collisions or external fields.
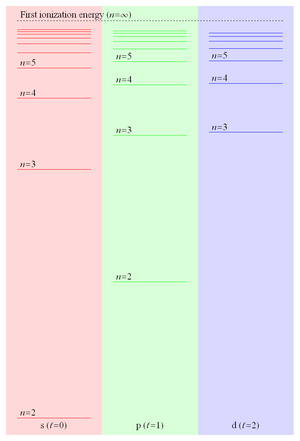
Because the binding energy of a Rydberg electron is proportional to 1/r and hence falls off like 1/n2, the energy level spacing falls off like 1/n3 leading to ever more closely spaced levels converging on the first ionization energy. These closely spaced Rydberg states form what is commonly referred to as the Rydberg series. Figure 2 shows some of the energy levels of the lowest three values of orbital angular momentum in lithium.
History[edit]
The existence of the Rydberg series was first demonstrated in 1885 when Johann Balmer discovered a simple empirical formula for the wavelengths of light associated with transitions in atomic hydrogen. Three years later, the Swedish physicist Johannes Rydberg presented a generalized and more intuitive version of Balmer's formula that came to be known as the Rydberg formula. This formula indicated the existence of an infinite series of ever more closely spaced discrete energy levels converging on a finite limit.[6]
This series was qualitatively explained in 1913 by Niels Bohr with his semiclassical model of the hydrogen atom in which quantized values of angular momentum lead to the observed discrete energy levels.[7][8] A full quantitative derivation of the observed spectrum was derived by Wolfgang Pauli in 1926 following development of quantum mechanics by Werner Heisenberg and others.
Methods of production[edit]
The only truly stable state of a hydrogen-like atom is the ground state with n = 1. The study of Rydberg states requires a reliable technique for exciting ground state atoms to states with a large value of n.
Electron impact excitation[edit]
Much early experimental work on Rydberg atoms relied on the use of collimated beams of fast electrons incident on ground-state atoms.[9] Inelastic scattering processes can use the electron kinetic energy to increase the atoms' internal energy exciting to a broad range of different states including many high-lying Rydberg states,
- .
Because the electron can retain any arbitrary amount of its initial kinetic energy, this process results in a population with a broad spread of different energies.
Charge exchange excitation[edit]
Another mainstay of early Rydberg atom experiments relied on charge exchange between a beam of ions and a population of neutral atoms of another species, resulting in the formation of a beam of highly excited atoms,[10]
- .
Again, because the kinetic energy of the interaction can contribute to the final internal energies of the constituents, this technique populates a broad range of energy levels.
Optical excitation[edit]
The arrival of tunable dye lasers in the 1970s allowed a much greater level of control over populations of excited atoms. In optical excitation, the incident photon is absorbed by the target atom, resulting in a precise final state energy. The problem of producing single state, mono-energetic populations of Rydberg atoms thus becomes the somewhat simpler problem of precisely controlling the frequency of the laser output,
- .
This form of direct optical excitation is generally limited to experiments with the alkali metals, because the ground state binding energy in other species is generally too high to be accessible with most laser systems.
For atoms with a large valence electron binding energy (equivalent to a large first ionization energy), the excited states of the Rydberg series are inaccessible with conventional laser systems. Initial collisional excitation can make up the energy shortfall allowing optical excitation to be used to select the final state. Although the initial step excites to a broad range of intermediate states, the precision inherent in the optical excitation process means that the laser light only interacts with a specific subset of atoms in a particular state, exciting to the chosen final state.
Hydrogenic potential[edit]

An atom in a Rydberg state has a valence electron in a large orbit far from the ion core; in such an orbit, the outermost electron feels an almost hydrogenic Coulomb potential, UC, from a compact ion core consisting of a nucleus with Z protons and the lower electron shells filled with Z-1 electrons. An electron in the spherically symmetric Coulomb potential has potential energy:
- .
The similarity of the effective potential "seen" by the outer electron to the hydrogen potential is a defining characteristic of Rydberg states and explains why the electron wavefunctions approximate to classical orbits in the limit of the correspondence principle.[11] In other words, the electron's orbit resembles the orbit of planets inside a solar system, similar to what was seen in the obsolete but visually useful Bohr and Rutherford models of the atom.
There are three notable exceptions that can be characterized by the additional term added to the potential energy:
- An atom may have two (or more) electrons in highly excited states with comparable orbital radii. In this case, the electron-electron interaction gives rise to a significant deviation from the hydrogen potential.[12] For an atom in a multiple Rydberg state, the additional term, Uee, includes a summation of each pair of highly excited electrons:
- .
- If the valence electron has very low angular momentum (interpreted classically as an extremely eccentric elliptical orbit), then it may pass close enough to polarise the ion core, giving rise to a 1/r4 core polarization term in the potential.[13] The interaction between an induced dipole and the charge that produces it is always attractive so this contribution is always negative,
- ,
- where αd is the dipole polarizability. Figure 3 shows how the polarization term modifies the potential close to the nucleus.
- If the outer electron penetrates the inner electron shells, it will “see” more of the charge of the nucleus and hence experience a greater force. In general, the modification to the potential energy is not simple to calculate and must be based on knowledge of the geometry of the ion core.[14]
Quantum-mechanical details[edit]
Quantum-mechanically, a state with abnormally high n refers to an atom in which the valence electron(s) have been excited into a formerly unpopulated electron orbital with higher energy and lower binding energy. In hydrogen the binding energy is given by:
- ,
where Ry = 13.6 eV is the Rydberg constant. The low binding energy at high values of n explains why Rydberg states are susceptible to ionization.
Additional terms in the potential energy expression for a Rydberg state, on top of the hydrogenic Coulomb potential energy require the introduction of a quantum defect,[5] δl, into the expression for the binding energy:
- .
Electron wavefunctions[edit]
The long lifetimes of Rydberg states with high orbital angular momentum can be explained in terms of the overlapping of wavefunctions. The wavefunction of an electron in a high l state (high angular momentum, “circular orbit”) has very little overlap with the wavefunctions of the inner electrons and hence remains relatively unperturbed.
The three exceptions to the definition of a Rydberg atom as an atom with a hydrogenic potential, have an alternative, quantum mechanical description that can be characterized by the additional term(s) in the atomic Hamiltonian:
- If a second electron is excited into a state ni, energetically close to the state of the outer electron no, then its wavefunction becomes almost as large as the first (a double Rydberg state). This occurs as ni approaches no and leads to a condition where the size of the two electron’s orbits are related;[12] a condition sometimes referred to as radial correlation.[1] An electron-electron repulsion term must be included in the atomic Hamiltonian.
- Polarization of the ion core produces an anisotropic potential that causes an angular correlation between the motions of the two outermost electrons.[1][15] This can be thought of as a tidal locking effect due to a non-spherically symmetric potential. A core polarization term must be included in the atomic Hamiltonian.
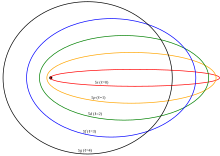
- The wavefunction of the outer electron in states with low orbital angular momentum l, is periodically localised within the shells of inner electrons and interacts with the full charge of the nucleus.[14] Figure 4 shows a semi-classical interpretation of angular momentum states in an electron orbital, illustrating that low-l states pass closer to the nucleus potentially penetrating the ion core. A core penetration term must be added to the atomic Hamiltonian.
In external fields[edit]
The large separation between the electron and ion-core in a Rydberg atom makes possible an extremely large electric dipole moment, d. There is an energy associated with the presence of an electric dipole in an electric field, F, known in atomic physics as a Stark shift,
Depending on the sign of the projection of the dipole moment onto the local electric field vector, a state may have energy that increases or decreases with field strength (low-field and high-field seeking states respectively). The narrow spacing between adjacent n-levels in the Rydberg series means that states can approach degeneracy even for relatively modest field strengths. The theoretical field strength at which a crossing would occur assuming no coupling between the states is given by the Inglis–Teller limit,[17]
In the hydrogen atom, the pure 1/r Coulomb potential does not couple Stark states from adjacent n-manifolds resulting in real crossings as shown in figure 5. The presence of additional terms in the potential energy can lead to coupling resulting in avoided crossings as shown for lithium in figure 6.
Applications and further research[edit]
Precision measurements of trapped Rydberg atoms[edit]
The radiative decay lifetimes of atoms in metastable states to the ground state are important to understanding astrophysics observations and tests of the standard model.[18]
Investigating diamagnetic effects[edit]
The large sizes and low binding energies of Rydberg atoms lead to a high magnetic susceptibility, . As diamagnetic effects scale with the area of the orbit and the area is proportional to the radius squared (A ∝ n4), effects impossible to detect in ground state atoms become obvious in Rydberg atoms, which demonstrate very large diamagnetic shifts.[19]
Rydberg atoms exhibit strong electric-dipole coupling of the atoms to electromagnetic fields and has been used to detect radio communications.[20][21]
In plasmas[edit]
Rydberg atoms form commonly in plasmas due to the recombination of electrons and positive ions; low energy recombination results in fairly stable Rydberg atoms, while recombination of electrons and positive ions with high kinetic energy often form autoionising Rydberg states. Rydberg atoms’ large sizes and susceptibility to perturbation and ionisation by electric and magnetic fields, are an important factor determining the properties of plasmas.[22]
Condensation of Rydberg atoms forms Rydberg matter, most often observed in form of long-lived clusters. The de-excitation is significantly impeded in Rydberg matter by exchange-correlation effects in the non-uniform electron liquid formed on condensation by the collective valence electrons, which causes extended lifetime of clusters.[23]
In astrophysics (Radio recombination lines)[edit]
Rydberg atoms occur in space due to the dynamic equilibrium between photoionization by hot stars and recombination with electrons, which at these very low densities usually proceeds via the electron re-joining the atom in a very high n state, and then gradually dropping through the energy levels to the ground state, giving rise to a sequence of recombination spectral lines spread across the electromagnetic spectrum. The very small differences in energy between Rydberg states differing in n by one or a few means that photons emitted in transitions between such states have low frequencies and long wavelengths, even up to radio waves. The first detection of such a radio recombination line (RRL) was by Soviet radio astronomers in 1964; the line, designated H90α, was emitted by hydrogen atoms in the n = 90 state. [24] Today, Rydberg atoms of hydrogen, helium and carbon in space are routinely observed via RRLs, the brightest of which are the Hnα lines corresponding to transitions from n+1 to n. Weaker lines, Hnβ and Hnγ, with Δn = 2 and 3 are also observed. Corresponding lines for helium and carbon are Henα, Cnα, and so on.[25] The discovery of lines with n > 100 was surprising, as even in the very low densities of interstellar space, many orders of magnitude lower than the best laboratory vacuums attainable on Earth, it had been expected that such highly-excited atoms would be frequently destroyed by collisions, rendering the lines unobservable. Improved theoretical analysis showed that this effect had been overestimated, although collisional broadening does eventually limit detectability of the lines at very high n..[25] The record wavelength for hydrogen is λ = 73 cm for H253α, implying atomic diameters of a few microns, and for carbon, λ = 18 metres, from C732α,[26] from atoms with a diameter of 57 micron.
RRLs from hydrogen and helium are produced in highly ionized regions (H II regions and the Warm Ionised Medium). Carbon has a lower ionization energy than hydrogen, and so singly-ionized carbon atoms, and the corresponding recombining Rydberg states, exist further from the ionizing stars, in so-called C II regions which form thick shells around H II regions. The larger volume partially compensates for the low abundance of C compared to H, making the carbon RRLs detectable.
In the absence of collisional broadening, the wavelengths of RRLs are modified only by the Doppler effect, so the measured wavelength, , is usually converted to radial velocity, , where is the rest-frame wavelength. H II regions in our Galaxy can have radial velocities up to ±150 km/s, due to their motion relative to Earth as both orbit the centre of the Galaxy.[27] These motions are regular enough that can be used to estimate the position of the H II region on the line of sight and so its 3D position in the Galaxy. Because all astrophysical Rydberg atoms are hydrogenic, the frequencies of transitions for H, He, and C are given by the same formula, except for the slightly different reduced mass of the valence electron for each element. This gives helium and carbon lines apparent Doppler shifts of −100 and −140 km/s, respectively, relative to the corresponding hydrogen line.
RRLs are used to detect ionized gas in distant regions of our Galaxy, and also in external galaxies, because the radio photons are not absorbed by interstellar dust, which blocks photons from the more familiar optical transitions.[28] They are also used to measure the temperature of the ionized gas, via the ratio of line intensity to the continuum bremsstrahlung emission from the plasma.[25] Since the temperature of H II regions is regulated by line emission from heavier elements such as C, N, and O, recombination lines also indirectly measure their abundance (metallicity). [29]
RRLs are spread across the radio spectrum with relatively small intervals in wavelength between them, so they frequently occur in radio spectral observations primarily targeted at other spectral lines. For instance, H166α, H167α, and H168α are very close in wavelength to the 21-cm line from neutral hydrogen. This allows radio astronomers to study both the neutral and the ionized interstellar medium from the same set of observations.[30] Since RRLs are numerous and weak, common practice is to average the velocity spectra of several neighbouring lines, to improve sensitivity.
There are a variety of other potential applications of Rydberg atoms in cosmology and astrophysics.[31]
Strongly interacting systems[edit]
Due to their large size, Rydberg atoms can exhibit very large electric dipole moments. Calculations using perturbation theory show that this results in strong interactions between two close Rydberg atoms. Coherent control of these interactions combined with their relatively long lifetime makes them a suitable candidate to realize a quantum computer.[32] In 2010 two-qubit gates were achieved experimentally.[33][34] Strongly interacting Rydberg atoms also feature quantum critical behavior, which makes them interesting to study on their own.[35]
Current research directions[edit]
Since 2000's Rydberg atoms research encompasses broadly five directions: sensing, quantum optics,[36][37][38][39][40][41] quantum computation,[42][43][44][45] quantum simulation[46][2][47][48] and quantum matters.[49][50] High electric dipole moments between Rydberg atomic states are used for radio frequency and terahertz sensing and imaging,[51][52] including non-demolition measurements of individual microwave photons.[53] Electromagnetically induced transparency was used in combination with strong interactions between two atoms excited in Rydberg state to provide medium that exhibits strongly nonlinear behaviour at the level of individual optical photons.[54][55] The tuneable interaction between Rydberg states, enabled also first quantum simulation experiments.[56][57]
In October 2018, the United States Army Research Laboratory publicly discussed efforts to develop a super wideband radio receiver using Rydberg atoms.[58] In March 2020, the laboratory announced that its scientists analysed the Rydberg sensor's sensitivity to oscillating electric fields over an enormous range of frequencies—from 0 to 1012 Hertz (the spectrum to 0.3mm wavelength). The Rydberg sensor can reliably detect signals over the entire spectrum and compare favourably with other established electric field sensor technologies, such as electro-optic crystals and dipole antenna-coupled passive electronics.[59][60]
Classical simulation[edit]


A simple 1/r potential results in a closed Keplerian elliptical orbit. In the presence of an external electric field Rydberg atoms can obtain very large electric dipole moments making them extremely susceptible to perturbation by the field. Figure 7 shows how application of an external electric field (known in atomic physics as a Stark field) changes the geometry of the potential, dramatically changing the behaviour of the electron. A Coulombic potential does not apply any torque as the force is always antiparallel to the position vector (always pointing along a line running between the electron and the nucleus):
- ,
- .
With the application of a static electric field, the electron feels a continuously changing torque. The resulting trajectory becomes progressively more distorted over time, eventually going through the full range of angular momentum from L = LMAX, to a straight line L=0, to the initial orbit in the opposite sense L = -LMAX.[61]
The time period of the oscillation in angular momentum (the time to complete the trajectory in figure 8), almost exactly matches the quantum mechanically predicted period for the wavefunction to return to its initial state, demonstrating the classical nature of the Rydberg atom.
See also[edit]
References[edit]
- ^ a b c Gallagher, Thomas F. (1994). Rydberg Atoms. Cambridge University Press. ISBN 978-0-521-02166-1.
- ^ a b Šibalić, Nikola; S Adams, Charles (2018). Rydberg Physics. IOP Publishing. Bibcode:2018ryph.book.....S. doi:10.1088/978-0-7503-1635-4. ISBN 9780750316354.
- ^ Metcalf Research Group (2004-11-08). "Rydberg Atom Optics". Stony Brook University. Archived from the original on August 26, 2005. Retrieved 2008-07-30.
- ^ J. Murray-Krezan (2008). "The classical dynamics of Rydberg Stark atoms in momentum space". American Journal of Physics. 76 (11): 1007–1011. Bibcode:2008AmJPh..76.1007M. doi:10.1119/1.2961081.
- ^ a b Nolan, James (2005-05-31). "Rydberg Atoms and the Quantum Defect". Davidson College. Archived from the original on 2015-12-06. Retrieved 2008-07-30.
- ^ I. Martinson; et al. (2005). "Janne Rydberg – his life and work". Nuclear Instruments and Methods in Physics Research Section B. 235 (1–4): 17–22. Bibcode:2005NIMPB.235...17M. doi:10.1016/j.nimb.2005.03.137.
- ^ "The Bohr Model". University of Tennessee, Knoxville. 2000-08-10. Retrieved 2009-11-25.
- ^ Niels Bohr (1922-12-11). "The Structure of the Atom" (PDF). Nobel Lecture. Retrieved 2018-11-16.
- ^ J. Olmsted (1967). "Excitation of nitrogen triplet states by electron impact". Radiation Research. 31 (2): 191–200. Bibcode:1967RadR...31..191O. doi:10.2307/3572319. JSTOR 3572319. PMID 6025857.
- ^ M. Haugh, et al. (1966). "Electronic excitation accompanying charge exchange". Journal of Chemical Physics. 44 (2): 837–839. Bibcode:1966JChPh..44..837H. doi:10.1063/1.1726773.
- ^ T. P. Hezel, et al. (1992). "Classical view of the properties of Rydberg atoms: Application of the correspondence principle". American Journal of Physics. 60 (4): 329–335. Bibcode:1992AmJPh..60..329H. doi:10.1119/1.16876.
- ^ a b I. K. Dmitrieva; et al. (1993). "Energies of Doubly Excited States. The Double Rydberg Formula". Journal of Applied Spectroscopy. 59 (1–2): 466–470. Bibcode:1993JApSp..59..466D. doi:10.1007/BF00663353. S2CID 96628309.
- ^ L. Neale; et al. (1995). "Core Polarization in Kr VIII". Physical Review A. 51 (5): 4272–4275. Bibcode:1995PhRvA..51.4272N. doi:10.1103/PhysRevA.51.4272. PMID 9912104.
- ^ a b C. E. Theodosiou (1983). "Evaluation of penetration effects in high-l Rydberg states". Physical Review A. 28 (5): 3098–3101. Bibcode:1983PhRvA..28.3098T. doi:10.1103/PhysRevA.28.3098.
- ^ T. A. Heim; et al. (1995). "Excitation of high-lying pair-Rydberg states". Journal of Physics B. 28 (24): 5309–5315. Bibcode:1995JPhB...28.5309H. doi:10.1088/0953-4075/28/24/015. S2CID 250862926.
- ^ a b M. Courtney, et al. (1995). "Classical, semiclassical, and quantum dynamics of lithium in an electric field". Physical Review A. 51 (5): 3604–3620. Bibcode:1995PhRvA..51.3604C. doi:10.1103/PhysRevA.51.3604. PMID 9912027.
- ^ D.R. Inglis; et al. (1939). "Ionic Depression of Series Limits in One-Electron Spectra". Astrophysical Journal. 90: 439. Bibcode:1939ApJ....90..439I. doi:10.1086/144118.
- ^ Nicholas D. Guise; et al. (Apr 24, 2014). "Measurement of the Kr xviii 3d 2D5/2 lifetime at low energy in a unitary Penning trap". Physical Review A. 89 (4): 040502. arXiv:1404.6181. Bibcode:2014PhRvA..89d0502G. doi:10.1103/PhysRevA.89.040502. S2CID 54090132.
- ^ J. Neukammer, et al. (1984). "Diamagnetic shift and singlet-triplet mixing of 6snp Yb Rydberg states with large radial extent". Physical Review A. 30 (2): 1142–1144. Bibcode:1984PhRvA..30.1142N. doi:10.1103/PhysRevA.30.1142.
- ^ Anderson, David A.; et al. (2021). "An Atomic Receiver for AM and FM Radio Communication". IEEE Transactions on Antennas and Propagation. 69 (5): 2455–2462. arXiv:1808.08589. Bibcode:2021ITAP...69.2455A. doi:10.1109/TAP.2020.2987112. S2CID 118828101.
- ^ Oullette, Jennifer (19 September 2018). "A new antenna using single atoms could usher in the age of atomic radio". Ars Technica. Retrieved 19 September 2018.
- ^ G. Vitrant, et al. (1982). "Rydberg to plasma evolution in a dense gas of very excited atoms". Journal of Physics B. 15 (2): L49–L55. Bibcode:1982JPhB...15L..49V. doi:10.1088/0022-3700/15/2/004.
- ^ E. A. Manykin, et al. (2006). "Rydberg matter: properties and decay". Proceedings of the SPIE. SPIE Proceedings. 6181 (5): 618105–618105–9. Bibcode:2006SPIE.6181E..05M. doi:10.1117/12.675004. S2CID 96732651.
- ^ Sorochenko, R. L.; Borodzich, É. V. (1965). "Detection of a Radio Line Due to Excited Hydrogen in the Nebula NGC 6618 (Omega)". Soviet Physics Doklady. 10: 588. Bibcode:1966SPhD...10..588S.
- ^ a b c Gordon, M.A.; Sorochenko, R.L. (2009). "Radio Recombination Lines". Astrophysics and Space Science Library. 282. doi:10.1007/978-0-387-09691-9. ISBN 978-0-387-09604-9. ISSN 0067-0057.
- ^ Konovalenko, A. A. (1984). "Observations of carbon recombination lines at decametric wavelengths in the direction of Cassiopeia". Pisma V Astronomicheskii Zhurnal (Soviet Astronomy Letters). 10: 353–356. Bibcode:1984PAZh...10..846K.
- ^ Wenger, Trey V.; Dawson, J. R.; Dickey, John M.; Jordan, C. H.; McClure–Griffiths, N. M.; Anderson, L. D.; Armentrout, W. P.; Balser, Dana S.; Bania, T. M. (2021-06-01). "The Southern H II Region Discovery Survey. II. The Full Catalog". The Astrophysical Journal Supplement Series. 254 (2): 36. arXiv:2103.12199. Bibcode:2021ApJS..254...36W. doi:10.3847/1538-4365/abf4d4. hdl:1885/287773. ISSN 0067-0049.
- ^ Anderson, L. D.; Luisi, Matteo; Liu, Bin; Wenger, Trey V.; Balser, Dana. S.; Bania, T. M.; Haffner, L. M.; Linville, Dylan J.; Mascoop, J. L. (2021-06-01). "The GBT Diffuse Ionized Gas Survey (GDIGS): Survey Overview and First Data Release". The Astrophysical Journal Supplement Series. 254 (2): 28. arXiv:2103.10466. Bibcode:2021ApJS..254...28A. doi:10.3847/1538-4365/abef65. ISSN 0067-0049.
- ^ Wenger, Trey V.; Balser, Dana S.; Anderson, L. D.; Bania, T. M. (2019-12-16). "Metallicity Structure in the Milky Way Disk Revealed by Galactic H ii Regions". The Astrophysical Journal. 887 (2): 114. arXiv:1910.14605. Bibcode:2019ApJ...887..114W. doi:10.3847/1538-4357/ab53d3. ISSN 1538-4357.
- ^ Alves, Marta I. R.; Calabretta, Mark; Davies, Rodney D.; Dickinson, Clive; Staveley-Smith, Lister; Davis, Richard J.; Chen, Tianyue; Barr, Adam (2015-06-21). "The HIPASS survey of the Galactic plane in radio recombination lines". Monthly Notices of the Royal Astronomical Society. 450 (2): 2025–2042. arXiv:1411.4497. doi:10.1093/mnras/stv751. ISSN 1365-2966.
- ^ Y. N. Gnedin, et al. (2009). "Rydberg atoms in astrophysics". New Astronomy Reviews. 53 (7–10): 259–265. arXiv:1208.2516. Bibcode:2009NewAR..53..259G. doi:10.1016/j.newar.2009.07.003. S2CID 119276100.
- ^ D. Jaksch, et al. (2000). "Fast Quantum Gates for Neutral Atoms". Physical Review Letters. 85 (10): 2208–11. arXiv:quant-ph/0004038. Bibcode:2000PhRvL..85.2208J. doi:10.1103/PhysRevLett.85.2208. PMID 10970499. S2CID 16713798.
- ^ T. Wilk, et al. (2010). "Entanglement of Two Individual Neutral Atoms Using Rydberg Blockade". Physical Review Letters. 104 (1): 010502. arXiv:0908.0454. Bibcode:2010PhRvL.104a0502W. doi:10.1103/PhysRevLett.104.010502. PMID 20366354. S2CID 16384272.
- ^ L. Isenhower, et al. (2010). "Demonstration of a Neutral Atom Controlled-NOT Quantum Gate". Physical Review Letters. 104 (1): 010503. arXiv:0907.5552. Bibcode:2010PhRvL.104a0503I. doi:10.1103/PhysRevLett.104.010503. PMID 20366355. S2CID 2091127.
- ^ H. Weimer, et al. (2008). "Quantum Critical Behavior in Strongly Interacting Rydberg Gases". Physical Review Letters. 101 (25): 250601. arXiv:0806.3754. Bibcode:2008PhRvL.101y0601W. doi:10.1103/PhysRevLett.101.250601. PMID 19113686. S2CID 28636728.
- ^ Tiarks, Daniel; Schmidt-Eberle, Steffen; Stolz, Thomas; Rempe, Gerhard; Dürr, Stephan (February 2019). "A photon–photon quantum gate based on Rydberg interactions". Nature Physics. 15 (2): 124–126. arXiv:1807.05795. doi:10.1038/s41567-018-0313-7. ISSN 1745-2473. S2CID 54072181.
- ^ Khazali, Mohammadsadegh; Murray, Callum R.; Pohl, Thomas (2019-09-13). "Polariton Exchange Interactions in Multichannel Optical Networks". Physical Review Letters. 123 (11): 113605. arXiv:1903.12442. Bibcode:2019PhRvL.123k3605K. doi:10.1103/PhysRevLett.123.113605. ISSN 0031-9007. PMID 31573258. S2CID 202577976.
- ^ Gorshkov, Alexey V.; Otterbach, Johannes; Fleischhauer, Michael; Pohl, Thomas; Lukin, Mikhail D. (2011-09-22). "Photon-Photon Interactions via Rydberg Blockade". Physical Review Letters. 107 (13): 133602. arXiv:1103.3700. Bibcode:2011PhRvL.107m3602G. doi:10.1103/physrevlett.107.133602. ISSN 0031-9007. PMID 22026852. S2CID 11681713.
- ^ Khazali, Mohammadsadegh; Heshami, Khabat; Simon, Christoph (2015-03-17). "Photon-photon gate via the interaction between two collective Rydberg excitations". Physical Review A. 91 (3): 030301. arXiv:1407.7510. Bibcode:2015PhRvA..91c0301K. doi:10.1103/physreva.91.030301. ISSN 1050-2947. S2CID 118859994.
- ^ Friedler, Inbal; Petrosyan, David; Fleischhauer, Michael; Kurizki, Gershon (2005-10-05). "Long-range interactions and entanglement of slow single-photon pulses". Physical Review A. 72 (4): 043803. arXiv:quant-ph/0503071. Bibcode:2005PhRvA..72d3803F. doi:10.1103/physreva.72.043803. ISSN 1050-2947. S2CID 30993913.
- ^ Paredes-Barato, D.; Adams, C. S. (2014-01-28). "All-Optical Quantum Information Processing Using Rydberg Gates". Physical Review Letters. 112 (4): 040501. arXiv:1309.7933. Bibcode:2014PhRvL.112d0501P. doi:10.1103/physrevlett.112.040501. ISSN 0031-9007. PMID 24580425. S2CID 19020862.
- ^ Lukin, M. D.; Fleischhauer, M.; Cote, R.; Duan, L. M.; Jaksch, D.; Cirac, J. I.; Zoller, P. (2001-06-26). "Dipole Blockade and Quantum Information Processing in Mesoscopic Atomic Ensembles". Physical Review Letters. 87 (3): 037901. arXiv:quant-ph/0011028. Bibcode:2001PhRvL..87c7901L. doi:10.1103/physrevlett.87.037901. ISSN 0031-9007. PMID 11461592. S2CID 13452668.
- ^ Jaksch, D.; Cirac, J. I.; Zoller, P.; Rolston, S. L.; Côté, R.; Lukin, M. D. (2000-09-04). "Fast Quantum Gates for Neutral Atoms". Physical Review Letters. 85 (10): 2208–2211. arXiv:quant-ph/0004038. Bibcode:2000PhRvL..85.2208J. doi:10.1103/physrevlett.85.2208. ISSN 0031-9007. PMID 10970499. S2CID 16713798.
- ^ Saffman, M.; Walker, T. G.; Mølmer, K. (2010-08-18). "Quantum information with Rydberg atoms". Reviews of Modern Physics. 82 (3): 2313–2363. arXiv:0909.4777. Bibcode:2010RvMP...82.2313S. doi:10.1103/revmodphys.82.2313. ISSN 0034-6861. S2CID 14285764.
- ^ Khazali, Mohammadsadegh; Mølmer, Klaus (2020-06-11). "Fast Multiqubit Gates by Adiabatic Evolution in Interacting Excited-State Manifolds of Rydberg Atoms and Superconducting Circuits". Physical Review X. 10 (2): 021054. arXiv:2006.07035. Bibcode:2020PhRvX..10b1054K. doi:10.1103/physrevx.10.021054. ISSN 2160-3308.
- ^ Weimer, Hendrik; Müller, Markus; Lesanovsky, Igor; Zoller, Peter; Büchler, Hans Peter (2010-03-14). "A Rydberg quantum simulator". Nature Physics. 6 (5): 382–388. arXiv:0907.1657. Bibcode:2010NatPh...6..382W. doi:10.1038/nphys1614. ISSN 1745-2473. S2CID 54710282.
- ^ Khazali, Mohammadsadegh (2022-03-03). "Discrete-Time Quantum-Walk & Floquet Topological Insulators via Distance-Selective Rydberg-Interaction". Quantum. 6: 664. arXiv:2101.11412. Bibcode:2022Quant...6..664K. doi:10.22331/q-2022-03-03-664. S2CID 246635019.
- ^ Dauphin, A.; Müller, M.; Martin-Delgado, M. A. (2012-11-20). "Rydberg-atom quantum simulation and Chern-number characterization of a topological Mott insulator". Physical Review A. 86 (5): 053618. arXiv:1207.6373. Bibcode:2012PhRvA..86e3618D. doi:10.1103/physreva.86.053618. ISSN 1050-2947. S2CID 55200016.
- ^ Khazali, Mohammadsadegh (2021-08-05). "Rydberg noisy dressing and applications in making soliton molecules and droplet quasicrystals". Physical Review Research. 3 (3): L032033. arXiv:2007.01039. Bibcode:2021PhRvR...3c2033K. doi:10.1103/PhysRevResearch.3.L032033. ISSN 2643-1564. S2CID 220301701.
- ^ Henkel, N.; Cinti, F.; Jain, P.; Pupillo, G.; Pohl, T. (2012-06-26). "Supersolid Vortex Crystals in Rydberg-Dressed Bose-Einstein Condensates". Physical Review Letters. 108 (26): 265301. arXiv:1111.5761. Bibcode:2012PhRvL.108z5301H. doi:10.1103/physrevlett.108.265301. ISSN 0031-9007. PMID 23004994. S2CID 1782501.
- ^ Sedlacek, Jonathon A.; Schwettmann, Arne; Kübler, Harald; Löw, Robert; Pfau, Tilman; Shaffer, James P. (2012-09-16). "Microwave electrometry with Rydberg atoms in a vapour cell using bright atomic resonances". Nature Physics. 8 (11): 819–824. Bibcode:2012NatPh...8..819S. doi:10.1038/nphys2423. ISSN 1745-2473. S2CID 121120666.
- ^ Wade, C. G.; Šibalić, N.; de Melo, N. R.; Kondo, J. M.; Adams, C. S.; Weatherill, K. J. (2016-11-07). "Real-time near-field terahertz imaging with atomic optical fluorescence". Nature Photonics. 11 (1): 40–43. arXiv:1603.07107. doi:10.1038/nphoton.2016.214. ISSN 1749-4885. S2CID 119212524.
- ^ Nogues, G.; Rauschenbeutel, A.; Osnaghi, S.; Brune, M.; Raimond, J. M.; Haroche, S. (1999). "Seeing a single photon without destroying it". Nature. 400 (6741): 239–242. Bibcode:1999Natur.400..239N. doi:10.1038/22275. ISSN 0028-0836. S2CID 4367650.
- ^ Pritchard, J. D.; Maxwell, D.; Gauguet, A.; Weatherill, K. J.; Jones, M. P. A.; Adams, C. S. (2010-11-05). "Cooperative Atom-Light Interaction in a Blockaded Rydberg Ensemble". Physical Review Letters. 105 (19): 193603. arXiv:0911.3523. Bibcode:2010PhRvL.105s3603P. doi:10.1103/physrevlett.105.193603. ISSN 0031-9007. PMID 21231168. S2CID 12217031.
- ^ Firstenberg, Ofer; Peyronel, Thibault; Liang, Qi-Yu; Gorshkov, Alexey V.; Lukin, Mikhail D.; Vuletić, Vladan (2013-09-25). "Attractive photons in a quantum nonlinear medium" (PDF). Nature. 502 (7469): 71–75. Bibcode:2013Natur.502...71F. doi:10.1038/nature12512. hdl:1721.1/91605. ISSN 0028-0836. PMID 24067613. S2CID 1699899.
- ^ Schauß, P.; Zeiher, J.; Fukuhara, T.; Hild, S.; Cheneau, M.; Macrì, T.; Pohl, T.; Bloch, I.; Gross, C. (2015-03-27). "Crystallization in Ising quantum magnets". Science. 347 (6229): 1455–1458. arXiv:1404.0980. Bibcode:2015Sci...347.1455S. doi:10.1126/science.1258351. ISSN 0036-8075. PMID 25814579. S2CID 28102735.
- ^ Labuhn, Henning; Barredo, Daniel; Ravets, Sylvain; de Léséleuc, Sylvain; Macrì, Tommaso; Lahaye, Thierry; Browaeys, Antoine (2016). "Tunable two-dimensional arrays of single Rydberg atoms for realizing quantum Ising models". Nature. 534 (7609): 667–670. arXiv:1509.04543. Bibcode:2016Natur.534..667L. doi:10.1038/nature18274. ISSN 0028-0836. PMID 27281203. S2CID 4461633.
- ^ Army researchers make giant leap in quantum sensing, United States Army Research Laboratory, 2018-10-25
- ^ Scientists create quantum sensor that covers entire radio frequency spectrum, Phys.org/United States Army Research Laboratory, 2020-03-19
- ^ Meyer, David H.; Kunz, Paul D.; Cox, Kevin C. (2021). "Waveguide-Coupled Rydberg Spectrum Analyzer from 0 to 20 GHz". Physical Review Applied. 15 (1): 014053. arXiv:2009.14383. Bibcode:2021PhRvP..15a4053M. doi:10.1103/PhysRevApplied.15.014053. S2CID 222067191.
- ^ T. P. Hezel, et al. (1992). "Classical view of the Stark effect in hydrogen atoms". American Journal of Physics. 60 (4): 324–328. Bibcode:1992AmJPh..60..324H. doi:10.1119/1.16875.






















