Shearlet
In applied mathematical analysis, shearlets are a multiscale framework which allows efficient encoding of anisotropic features in multivariate problem classes. Originally, shearlets were introduced in 2006[1] for the analysis and sparse approximation of functions . They are a natural extension of wavelets, to accommodate the fact that multivariate functions are typically governed by anisotropic features such as edges in images, since wavelets, as isotropic objects, are not capable of capturing such phenomena.
Shearlets are constructed by parabolic scaling, shearing, and translation applied to a few generating functions. At fine scales, they are essentially supported within skinny and directional ridges following the parabolic scaling law, which reads length² ≈ width. Similar to wavelets, shearlets arise from the affine group and allow a unified treatment of the continuum and digital situation leading to faithful implementations. Although they do not constitute an orthonormal basis for , they still form a frame allowing stable expansions of arbitrary functions .
One of the most important properties of shearlets is their ability to provide optimally sparse approximations (in the sense of optimality in [2]) for cartoon-like functions . In imaging sciences, cartoon-like functions serve as a model for anisotropic features and are compactly supported in while being apart from a closed piecewise singularity curve with bounded curvature. The decay rate of the -error of the -term shearlet approximation obtained by taking the largest coefficients from the shearlet expansion is in fact optimal up to a log-factor:[3][4]
where the constant depends only on the maximum curvature of the singularity curve and the maximum magnitudes of , and . This approximation rate significantly improves the best -term approximation rate of wavelets providing only for such class of functions.
Shearlets are to date the only directional representation system that provides sparse approximation of anisotropic features while providing a unified treatment of the continuum and digital realm that allows faithful implementation. Extensions of shearlet systems to are also available. A comprehensive presentation of the theory and applications of shearlets can be found in.[5]
Definition[edit]
Continuous shearlet systems[edit]
The construction of continuous shearlet systems is based on parabolic scaling matrices
as a mean to change the resolution, on shear matrices
as a means to change the orientation, and finally on translations to change the positioning. In comparison to curvelets, shearlets use shearings instead of rotations, the advantage being that the shear operator leaves the integer lattice invariant in case , i.e., This indeed allows a unified treatment of the continuum and digital realm, thereby guaranteeing a faithful digital implementation.
For the continuous shearlet system generated by is then defined as
and the corresponding continuous shearlet transform is given by the map
Discrete shearlet systems[edit]
A discrete version of shearlet systems can be directly obtained from by discretizing the parameter set There are numerous approaches for this but the most popular one is given by
From this, the discrete shearlet system associated with the shearlet generator is defined by
and the associated discrete shearlet transform is defined by
Examples[edit]
Let be a function satisfying the discrete Calderón condition, i.e.,
with and where denotes the Fourier transform of For instance, one can choose to be a Meyer wavelet. Furthermore, let be such that and
One typically chooses to be a smooth bump function. Then given by
is called a classical shearlet. It can be shown that the corresponding discrete shearlet system constitutes a Parseval frame for consisting of bandlimited functions.[5]
Another example are compactly supported shearlet systems, where a compactly supported function can be chosen so that forms a frame for .[4][6][7][8] In this case, all shearlet elements in are compactly supported providing superior spatial localization compared to the classical shearlets, which are bandlimited. Although a compactly supported shearlet system does not generally form a Parseval frame, any function can be represented by the shearlet expansion due to its frame property.
Cone-adapted shearlets[edit]
One drawback of shearlets defined as above is the directional bias of shearlet elements associated with large shearing parameters. This effect is already recognizable in the frequency tiling of classical shearlets (see Figure in Section #Examples), where the frequency support of a shearlet increasingly aligns along the -axis as the shearing parameter goes to infinity. This causes serious problems when analyzing a function whose Fourier transform is concentrated around the -axis.
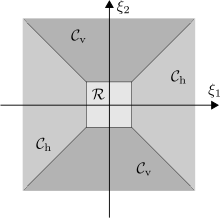
To deal with this problem, the frequency domain is divided into a low-frequency part and two conic regions (see Figure):

The associated cone-adapted discrete shearlet system consists of three parts, each one corresponding to one of these frequency domains. It is generated by three functions and a lattice sampling factor
where
with
The systems and basically differ in the reversed roles of and . Thus, they correspond to the conic regions and , respectively. Finally, the scaling function is associated with the low-frequency part .
Applications[edit]
- Image processing and computer sciences[5]
- PDEs[5]
- Resolution of the wavefront set
- Transport equations
- Coorbit theory, characterization of smoothness spaces[5]
- Differential geometry: manifold learning
Generalizations and extensions[edit]
See also[edit]
- Wavelet transform
- Curvelet transform
- Contourlet transform
- Bandelet transform
- Chirplet transform
- Noiselet transform
References[edit]
- ^ Guo, Kanghui, Gitta Kutyniok, and Demetrio Labate. "Sparse multidimensional representations using anisotropic dilation and shear operators." Wavelets and Splines (Athens, GA, 2005), G. Chen and MJ Lai, eds., Nashboro Press, Nashville, TN (2006): 189–201. "PDF" (PDF).
- ^ Donoho, David Leigh. "Sparse components of images and optimal atomic decompositions." Constructive Approximation 17.3 (2001): 353–382. "PDF". CiteSeerX 10.1.1.379.8993.
- ^ Guo, Kanghui, and Demetrio Labate. "Optimally sparse multidimensional representation using shearlets." SIAM Journal on Mathematical Analysis 39.1 (2007): 298–318. "PDF" (PDF).
- ^ a b Kutyniok, Gitta, and Wang-Q Lim. "Compactly supported shearlets are optimally sparse." Journal of Approximation Theory 163.11 (2011): 1564–1589. "PDF" (PDF).
- ^ a b c d e Kutyniok, Gitta, and Demetrio Labate, eds. Shearlets: Multiscale analysis for multivariate data. Springer, 2012, ISBN 0-8176-8315-1
- ^ Kittipoom, Pisamai, Gitta Kutyniok, and Wang-Q Lim. "Construction of compactly supported shearlet frames." Constructive Approximation 35.1 (2012): 21–72. Kittipoom, P.; Kutyniok, G.; Lim, W. (2010). "PDF". arXiv:1003.5481 [math.FA].
- ^ a b c Kutyniok, Gitta, Jakob Lemvig, and Wang-Q Lim. "Optimally sparse approximations of 3D functions by compactly supported shearlet frames." SIAM Journal on Mathematical Analysis 44.4 (2012): 2962–3017. Kutyniok, Gitta; Lemvig, Jakob; Lim, Wang-Q (2011). "PDF". arXiv:1109.5993 [math.FA].
- ^ Purnendu Banerjee and B. B. Chaudhuri, “Video Text Localization using Wavelet and Shearlet Transforms”, In Proc. SPIE 9021, Document Recognition and Retrieval XXI, 2014 (doi:10.1117/12.2036077).Banerjee, Purnendu; Chaudhuri, B. B. (2013). "Video text localization using wavelet and shearlet transforms". In Coüasnon, Bertrand; Ringger, Eric K (eds.). Document Recognition and Retrieval XXI. Vol. 9021. pp. 90210B. arXiv:1307.4990. doi:10.1117/12.2036077. S2CID 10659099.
- ^ Guo, Kanghui, and Demetrio Labate. "The construction of smooth Parseval frames of shearlets." Mathematical Modelling of Natural Phenomena 8.01 (2013): 82–105. "PDF" (PDF).
- ^ Grohs, Philipp and Kutyniok, Gitta. "Parabolic molecules." Foundations of Computational Mathematics (to appear) Grohs, Philipp; Kutyniok, Gitta (2012). "PDF". arXiv:1206.1958 [math.FA].
- ^ Easley, Glenn R.; Guo, Kanghui; Labate, Demetrio; Pahari, Basanta R. (2020-08-10). "Optimally Sparse Representations of Cartoon-Like Cylindrical Data". The Journal of Geometric Analysis. 39 (9): 8926–8946. doi:10.1007/s12220-020-00493-0. S2CID 221675372. Retrieved 2022-01-22.
- ^ Bernhard, Bernhard G.; Labate, Demetrio; Pahari, Basanta R. (2019-10-29). "Smooth projections and the construction of smooth Parseval frames of shearlets". Advances in Computational Mathematics. 45 (5–6): 3241–3264. doi:10.1007/s10444-019-09736-3. S2CID 210118010. Retrieved 2022-01-22.




![{\displaystyle [0,1]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e2fd6e9b0db782a26c033d7c728aadac9eec363a)






























![{\displaystyle \operatorname {supp} {\hat {\psi }}_{1}\subseteq [-{\tfrac {1}{2}},-{\tfrac {1}{16}}]\cup [{\tfrac {1}{16}},{\tfrac {1}{2}}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fd994a790ae83d9e4432998b8e148da9c2c7ba4)





![{\displaystyle \operatorname {supp} {\hat {\psi }}_{2}\subseteq [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be9d7048ed3022be72a06f098288a848f9feef6)
![{\displaystyle \sum _{k=-1}^{1}|{\hat {\psi }}_{2}(\xi +k)|^{2}=1,{\text{for a.e. }}\xi \in \left[-1,1\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fa08b5c6527adfc7cc1f2651b4b413109730f1e)



















