Thermoelectric effect
This article needs additional citations for verification. (November 2019) |
| Thermoelectric effect |
|---|
 |
The thermoelectric effect is the direct conversion of temperature differences to electric voltage and vice versa via a thermocouple.[1] A thermoelectric device creates a voltage when there is a different temperature on each side. Conversely, when a voltage is applied to it, heat is transferred from one side to the other, creating a temperature difference.
This effect can be used to generate electricity, measure temperature or change the temperature of objects. Because the direction of heating and cooling is affected by the applied voltage, thermoelectric devices can be used as temperature controllers.
The term "thermoelectric effect" encompasses three separately identified effects: the Seebeck effect (temperature differences cause electromotive forces), the Peltier effect (thermocouples create temperature differences), and the Thomson effect (the Seebeck coefficient varies with temperature). The Seebeck and Peltier effects are different manifestations of the same physical process; textbooks may refer to this process as the Peltier–Seebeck effect (the separation derives from the independent discoveries by French physicist Jean Charles Athanase Peltier and Baltic German physicist Thomas Johann Seebeck). The Thomson effect is an extension of the Peltier–Seebeck model and is credited to Lord Kelvin.
Joule heating, the heat that is generated whenever a current is passed through a conductive material, is not generally termed a thermoelectric effect. The Peltier–Seebeck and Thomson effects are thermodynamically reversible,[2] whereas Joule heating is not.
Origin
[edit]At the atomic scale, a temperature gradient causes charge carriers in the material to diffuse from the hot side to the cold side. This is due to charge carrier particles having higher mean velocities (and thus kinetic energy) at higher temperatures, leading them to migrate on average towards the colder side, in the process carrying heat across the material.[3]
Depending on the material properties and nature of the charge carriers (whether they are positive holes in a bulk material or electrons of negative charge), heat can be carried in either direction with respect to voltage. Semiconductors of n-type and p-type are often combined in series as they have opposite directions for heat transport, as specified by the sign of their Seebeck coefficients.[4]
Seebeck effect
[edit]
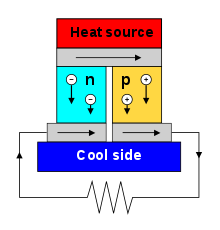
The Seebeck effect is the electromotive force (emf) that develops across two points of an electrically conducting material when there is a temperature difference between them. The emf is called the Seebeck emf (or thermo/thermal/thermoelectric emf). The ratio between the emf and temperature difference is the Seebeck coefficient. A thermocouple measures the difference in potential across a hot and cold end for two dissimilar materials. This potential difference is proportional to the temperature difference between the hot and cold ends. First discovered in 1794 by Italian scientist Alessandro Volta,[5][note 1] it is named after the Russian born, Baltic German physicist Thomas Johann Seebeck who rediscovered it in 1821.
Seebeck observed what he called "thermomagnetic effect" wherein a magnetic compass needle would be deflected by a closed loop formed by two different metals joined in two places, with an applied temperature difference between the joints. Danish physicist Hans Christian Ørsted noted that the temperature difference was in fact driving an electric current, with the generation of magnetic field being an indirect consequence, and so coined the more accurate term "thermoelectricity".[6]
The Seebeck effect is a classic example of an electromotive force (EMF) and leads to measurable currents or voltages in the same way as any other EMF. The local current density is given by
where is the local voltage,[7] and is the local conductivity. In general, the Seebeck effect is described locally by the creation of an electromotive field
where is the Seebeck coefficient (also known as thermopower), a property of the local material, and is the temperature gradient.
The Seebeck coefficients generally vary as function of temperature and depend strongly on the composition of the conductor. For ordinary materials at room temperature, the Seebeck coefficient may range in value from −100 μV/K to +1,000 μV/K (see Seebeck coefficient article for more information).
Applications
[edit]In practice, thermoelectric effects are essentially unobservable for a localized hot or cold spot in a single homogeneous conducting material, since the overall emfs from the increasing and decreasing temperature gradients will perfectly cancel out. Attaching an electrode to the hotspot in an attempt to measure the locally shifted voltage will only partly succeed: it means another temperature gradient will appear inside of the electrode, and so the overall emf will depend on the difference in Seebeck coefficients between the electrode and the conductor it is attached to.
Thermocouples involve two wires, each of a different material, that are electrically joined in a region of unknown temperature. The loose ends are measured in an open-circuit state (without any current, ). Although the materials' Seebeck coefficients are nonlinearly temperature dependent and different for the two materials, the open-circuit condition means that everywhere. Therefore (see the thermocouple article for more details) the voltage measured at the loose ends of the wires is directly dependent on the unknown temperature, and yet totally independent of other details such as the exact geometry of the wires. This direct relationship allows the thermocouple arrangement to be used as a straightforward uncalibrated thermometer, provided knowledge of the difference in -vs- curves of the two materials, and of the reference temperature at the measured loose wire ends.
Thermoelectric sorting functions similarly to a thermocouple but involves an unknown material instead of an unknown temperature: a metallic probe of known composition is kept at a constant known temperature and held in contact with the unknown sample that is locally heated to the probe temperature, thereby providing an approximate measurement of the unknown Seebeck coefficient . This can help distinguish between different metals and alloys.
Thermopiles are formed from many thermocouples in series, zig-zagging back and forth between hot and cold. This multiplies the voltage output.
Thermoelectric generators are like a thermocouple/thermopile but instead draw some current from the generated voltage in order to extract power from heat differentials. They are optimized differently from thermocouples, using high quality thermoelectric materials in a thermopile arrangement, to maximize the extracted power. Though not particularly efficient, these generators have the advantage of not having any moving parts.
Peltier effect
[edit]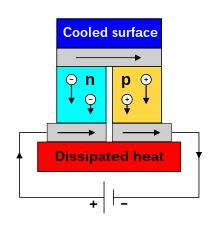
When an electric current is passed through a circuit of a thermocouple, heat is generated at one junction and absorbed at the other junction. This is known as the Peltier effect: the presence of heating or cooling at an electrified junction of two different conductors. The effect is named after French physicist Jean Charles Athanase Peltier, who discovered it in 1834.[8] When a current is made to flow through a junction between two conductors, A and B, heat may be generated or removed at the junction. The Peltier heat generated at the junction per unit time is
where and are the Peltier coefficients of conductors A and B, and is the electric current (from A to B). The total heat generated is not determined by the Peltier effect alone, as it may also be influenced by Joule heating and thermal-gradient effects (see below).
The Peltier coefficients represent how much heat is carried per unit charge. Since charge current must be continuous across a junction, the associated heat flow will develop a discontinuity if and are different. The Peltier effect can be considered as the back-action counterpart to the Seebeck effect (analogous to the back-EMF in magnetic induction): if a simple thermoelectric circuit is closed, then the Seebeck effect will drive a current, which in turn (by the Peltier effect) will always transfer heat from the hot to the cold junction. The close relationship between Peltier and Seebeck effects can be seen in the direct connection between their coefficients: (see below).
A typical Peltier heat pump involves multiple junctions in series, through which a current is driven. Some of the junctions lose heat due to the Peltier effect, while others gain heat. Thermoelectric heat pumps exploit this phenomenon, as do thermoelectric cooling devices found in refrigerators.
Applications
[edit]The Peltier effect can be used to create a heat pump. Notably, the Peltier thermoelectric cooler is a refrigerator that is compact and has no circulating fluid or moving parts. Such refrigerators are useful in applications where their advantages outweigh the disadvantage of their very low efficiency.
Other heat pump applications such as dehumidifiers may also use Peltier heat pumps.
Thermoelectric coolers are trivially reversible, in that they can be used as heaters by simply reversing the current. Unlike ordinary resistive electrical heating (Joule heating) that varies with the square of current, the thermoelectric heating effect is linear in current (at least for small currents) but requires a cold sink to replenish with heat energy. This rapid reversing heating and cooling effect is used by many modern thermal cyclers, laboratory devices used to amplify DNA by the polymerase chain reaction (PCR). PCR requires the cyclic heating and cooling of samples to specified temperatures. The inclusion of many thermocouples in a small space enables many samples to be amplified in parallel.
Thomson effect
[edit]For certain materials, the Seebeck coefficient is not constant in temperature, and so a spatial gradient in temperature can result in a gradient in the Seebeck coefficient. If a current is driven through this gradient, then a continuous version of the Peltier effect will occur. This Thomson effect was predicted and later observed in 1851 by Lord Kelvin (William Thomson).[9] It describes the heating or cooling of a current-carrying conductor with a temperature gradient. If a current density is passed through a homogeneous conductor, the Thomson effect predicts a heat production rate per unit volume.
where is the temperature gradient, and is the Thomson coefficient. The Thomson effect is a manifestation of the direction of flow of electrical carriers with respect to a temperature gradient within a conductor. These absorb energy (heat) flowing in a direction opposite to a thermal gradient, increasing their potential energy, and, when flowing in the same direction as a thermal gradient, they liberate heat, decreasing their potential energy.[10] The Thomson coefficient is related to the Seebeck coefficient as (see below). This equation, however, neglects Joule heating and ordinary thermal conductivity (see full equations below).
Full thermoelectric equations
[edit]Often, more than one of the above effects is involved in the operation of a real thermoelectric device. The Seebeck effect, Peltier effect, and Thomson effect can be gathered together in a consistent and rigorous way, described here; this also includes the effects of Joule heating and ordinary heat conduction. As stated above, the Seebeck effect generates an electromotive force, leading to the current equation[11]
To describe the Peltier and Thomson effects, we must consider the flow of energy. If temperature and charge change with time, the full thermoelectric equation for the energy accumulation, , is[11]
where is the thermal conductivity. The first term is the Fourier's heat conduction law, and the second term shows the energy carried by currents. The third term, , is the heat added from an external source (if applicable).
If the material has reached a steady state, the charge and temperature distributions are stable, so and . Using these facts and the second Thomson relation (see below), the heat equation can be simplified to
The middle term is the Joule heating, and the last term includes both Peltier ( at junction) and Thomson ( in thermal gradient) effects. Combined with the Seebeck equation for , this can be used to solve for the steady-state voltage and temperature profiles in a complicated system.
If the material is not in a steady state, a complete description needs to include dynamic effects such as relating to electrical capacitance, inductance and heat capacity.
The thermoelectric effects lie beyond the scope of equilibrium thermodynamics. They necessarily involve continuing flows of energy. At least, they involve three bodies or thermodynamic subsystems, arranged in a particular way, along with a special arrangement of the surroundings. The three bodies are the two different metals and their junction region. The junction region is an inhomogeneous body, assumed to be stable, not suffering amalgamation by diffusion of matter. The surroundings are arranged to maintain two temperature reservoirs and two electric reservoirs.
For an imagined, but not actually possible, thermodynamic equilibrium, heat transfer from the hot reservoir to the cold reservoir would need to be prevented by a specifically matching voltage difference maintained by the electric reservoirs, and the electric current would need to be zero. For a steady state, there must be at least some heat transfer or some non-zero electric current. The two modes of energy transfer, as heat and by electric current, can be distinguished when there are three distinct bodies and a distinct arrangement of surroundings.
But in the case of continuous variation in the media, heat transfer and thermodynamic work cannot be uniquely distinguished. This is more complicated than the often considered thermodynamic processes, in which just two respectively homogeneous subsystems are connected.
Thomson relations
[edit]In 1854, Lord Kelvin found relationships between the three coefficients, implying that the Thomson, Peltier, and Seebeck effects are different manifestations of one effect (uniquely characterized by the Seebeck coefficient).[12]
The first Thomson relation is[11]
where is the absolute temperature, is the Thomson coefficient, is the Peltier coefficient, and is the Seebeck coefficient. This relationship is easily shown given that the Thomson effect is a continuous version of the Peltier effect.
The second Thomson relation is
This relation expresses a subtle and fundamental connection between the Peltier and Seebeck effects. It was not satisfactorily proven until the advent of the Onsager relations, and it is worth noting that this second Thomson relation is only guaranteed for a time-reversal symmetric material; if the material is placed in a magnetic field or is itself magnetically ordered (ferromagnetic, antiferromagnetic, etc.), then the second Thomson relation does not take the simple form shown here.[13]
Now, using the second relation, the first Thomson relation becomes
The Thomson coefficient is unique among the three main thermoelectric coefficients because it is the only one directly measurable for individual materials. The Peltier and Seebeck coefficients can only be easily determined for pairs of materials; hence, it is difficult to find values of absolute Seebeck or Peltier coefficients for an individual material.
If the Thomson coefficient of a material is measured over a wide temperature range, it can be integrated using the Thomson relations to determine the absolute values for the Peltier and Seebeck coefficients. This needs to be done only for one material, since the other values can be determined by measuring pairwise Seebeck coefficients in thermocouples containing the reference material and then adding back the absolute Seebeck coefficient of the reference material. For more details on absolute Seebeck coefficient determination, see Seebeck coefficient.
See also
[edit]- Barocaloric material
- Nernst effect – a thermoelectric phenomenon when a sample allowing electrical conduction in a magnetic field and a temperature gradient normal (perpendicular) to each other
- Ettingshausen effect – thermoelectric phenomenon affecting current in a conductor in a magnetic field
- Pyroelectricity – the creation of an electric polarization in a crystal after heating/cooling, an effect distinct from thermoelectricity
- Thermionic emission – the liberation of charged particles from a hot electrode
- Thermogalvanic cell – the production of electrical power from a galvanic cell with electrodes at different temperatures
- Thermopile
- Thermophotovoltaic – production of electrical power from thermal energy using the photovoltaic effect
References
[edit]- ^ "The Peltier Effect and Thermoelectric Cooling". ffden-2.phys.uaf.edu.
- ^ As the "figure of merit" approaches infinity, the Peltier–Seebeck effect can drive a heat engine or refrigerator at closer and closer to the Carnot efficiency. Disalvo, F. J. (1999). "Thermoelectric Cooling and Power Generation". Science. 285 (5428): 703–706. doi:10.1126/science.285.5428.703. PMID 10426986. Any device that works at the Carnot efficiency is thermodynamically reversible, a consequence of classical thermodynamics.
- ^ "THERMOELECTRIC PHENOMENA" (PDF). Retrieved 2024-08-13.
- ^ Prunet, G.; Pawula, F.; Fleury, G.; Cloutet, E.; Robinson, A.J.; Hadziioannou, G.; Pakdel, A. (2021). "A review on conductive polymers and their hybrids for flexible and wearable thermoelectric applications" (PDF). Materials Today Physics. 18: 100402. Bibcode:2021MTPhy..1800402P. doi:10.1016/j.mtphys.2021.100402. hdl:2262/98609.
- ^ Goupil, Christophe; Ouerdane, Henni; Zabrocki, Knud; Seifert, Wolfgang; Hinsche, Nicki F.; Müller, Eckhard (2016). "Thermodynamics and thermoelectricity". In Goupil, Christophe (ed.). Continuum Theory and Modeling of Thermoelectric Elements. New York: Wiley-VCH. pp. 2–3. ISBN 9783527413379.
- ^ See:
- Œrsted (1823). "Nouvelles expériences de M. Seebeck sur les actions électro-magnetiques" [New experiments by Mr. Seebeck on electro-magnetic actions]. Annales de chimie. 2nd series (in French). 22: 199–201. From pp. 199–200: "Il faudra sans doute désormais distinguer cette nouvelle classes de circuits électriques par une dénomination significative; et comme telle je propose l'expression de circuits thermo-électriques ou peut-être thermélectriques … " (It's undoubtedly necessary to distinguish henceforth this new class of electrical circuits by an indicative name; and as such I propose the expression "thermo-electric circuits" or perhaps "thermelectric circuits" … )
- Oersted (1823). "Notiz von neuen electrisch-magnetischen Versuchen des Herrn Seebeck in Berlin" [Notice of new electro-magnetic experiments of Mr. Seebeck in Berlin]. Annalen der Physik (in German). 73 (4): 430–432. Bibcode:1823AnP....73..430O. doi:10.1002/andp.18230730410.
- ^ The voltage in this case does not refer to electric potential but rather the "voltmeter" voltage , where is the Fermi level.
- ^ Peltier (1834). "Nouvelles expériences sur la caloricité des courants électrique" [New experiments on the heat effects of electric currents]. Annales de Chimie et de Physique (in French). 56: 371–386.
- ^ Thomson, William (1857). "4. On a Mechanical Theory of Thermo-Electric Currents". Proceedings of the Royal Society of Edinburgh. 3. Cambridge Univ. Press: 91–98. doi:10.1017/S0370164600027310 (inactive 2024-11-11). Retrieved 7 February 2022.
{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link) - ^ Rowe, David Michael (1994). CRC Handbook of Thermoelectrics. Boca Raton New York London [etc.]: CRC press. ISBN 0849301467.
- ^ a b c Leon van Dommelen (2002-02-01). "A.11 Thermoelectric effects". eng.famu.fsu.edu. Retrieved 2022-11-23.
- ^ Thomson, William (1857). "On the dynamical theory of heat. Part V. Thermo-electric currents". Transactions of the Royal Society of Edinburgh. 21: 123–171. doi:10.1017/S0080456800032014. S2CID 120018011.
- ^ There is a generalized second Thomson relation relating anisotropic Peltier and Seebeck coefficients with reversed magnetic field and magnetic order. See, for example, Rowe, D. M., ed. (2010). Thermoelectrics Handbook: Macro to Nano. CRC Press. ISBN 9781420038903.
Notes
[edit]- ^ In 1794, Volta found that if a temperature difference existed between the ends of an iron rod, then it could excite spasms of a frog's leg. His apparatus consisted of two glasses of water. Dipped in each glass was a wire that was connected to one or the other hind leg of a frog. An iron rod was bent into a bow and one end was heated in boiling water. When the ends of the iron bow were dipped into the two glasses, a thermoelectric current passed through the frog's legs and caused them to twitch. See:
- Volta, Alessandro (1794). "Nuova memoria sull'elettricità animale del Sig. Don Alessandro Volta … in alcune lettere al Sig. Ab. Anton Maria Vassalli …" [New memoir on animal electricity from Don Alessandro Volta … in some letters to Abbot Antonio Maria Vassalli …]. Annali di Chimica e Storia Naturale (Annals of Chemistry and Natural History) (in Italian). 5: 132–144.; see p. 139.
- Reprinted in: Volta, Alessandro (1816) Collezione dell'Opere del Cavaliere Conte Alessandro Volta … [Collection of the works of Count Alessandro Volta … ]. (in Italian) Florence (Firenze), (Italy): Guglielmo Piatti. vol. 2, part 1. "Nuova memoria sull'elettricità animale, divisa in tre lettere, dirette al Signor Abate Anton Maria Vassalli … Lettera Prima" (New memoir on animal electricity, divided into three letters, addressed to Abbot Antonio Maria Vassalli … First letter), pp. 197–206; see p. 202.
Further reading
[edit]- Rowe, D.M., ed. (2006). Thermoelectrics Handbook:Macro to Nano. Taylor & Francis. doi:10.1201/9781420038903. ISBN 0-8493-2264-2. OCLC 70217582.
- Jack, P.M. (2003). "Physical Space as a Quaternion Structure I: Maxwell Equations. A Brief Note". arXiv:math-ph/0307038.
- Besançon, Robert M. (1985). Besançon, Robert M. (ed.). The Encyclopedia of Physics (3rd ed.). Van Nostrand Reinhold. doi:10.1007/978-1-4615-6902-2. ISBN 0-442-25778-3.
- Ioffe, A.F. (1957). Semiconductor Thermoelements and Thermoelectric Cooling. Infosearch. ISBN 0-85086-039-3. OCLC 600476276.
- Thomson, William (1851). "On a mechanical theory of thermo-electric currents". Proceedings of the Royal Society of Edinburgh. 3 (published 1857): 91–98. doi:10.1017/S0370164600027310 (inactive 2024-11-11).
{{cite journal}}: CS1 maint: DOI inactive as of November 2024 (link)
External links
[edit]- International Thermoelectric Society
- Föll, Helmut (Oct 2019). "2.3.3 Thermoelectric Effects: General Consideration". Electronic Materials. University of Kiel.
- A news article on the increases in thermal diode efficiency
































