User:Dave3457/Sandbox/Talk space referred

In the physics of wave propagation, a plane wave (also spelled planewave) is a constant-frequency wave whose wavefronts (surfaces of constant phase) are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector.

Animation of a 3D Plane wave.

The wavefronts of a plane wave traveling in 3-space

User:Dave3457 : Nothing above this has been changed.

It is not possible in practice to have a true plane wave; only a plane wave of infinite extent will propagate as a plane wave. However, many waves are approximately plane waves in a localized region of space. For example, a localized source such as an antenna produces a field that is approximately a plane wave far from the antenna in its far-field region. Similarly, if the length scales are much longer than the wavelength of the wave as is often the case for light in the field of optics, one can treat the waves as light rays which correspond locally to plane waves.

Laser beams are also approximately planar.

Mathematical formalisms

At time equals zero a positive phase shift results in the wave being shifted toward the left.

As t increases the wave travels to the right and the value at a given point x oscillates sinusoidally.

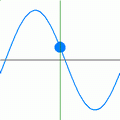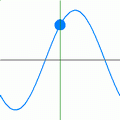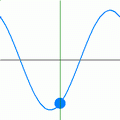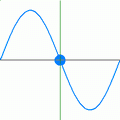
Two functions that meet the above criteria of having a constant frequency and constant amplitude are the sine and cosine functions. One of the simplest ways to use such a sinusoid involves defining it along the direction of the x-axis. The below equation, which is illustrated toward the right, uses the cosine function to represent a plane wave travelling in the positive x direction.

$A(x,t)=A_{o}\cos(kx-\omega t+\varphi )$

In the above equation…

• $A(x,t)\,\!$ is the magnitude or disturbance of the wave at a given point in space and time. An example would be to let $A(x,t)\,\!$ represent the variation of air pressure relative to the norm in the case of a sound wave.
• $A_{o}\,\!$ is the amplitude of the wave which is the peak magnitude of the oscillation.
• $k\,\!$ is the wave’s wave number or more specifically the angular wave number and equals $2\pi /\lambda \,\!$, where $\lambda \,\!$ is the wavelength of the wave. $k\,\!$ has the units of radians per unit distance and is a measure of how rapidly the disturbance changes over a length of distance at a particular point in time.
• $x\,\!$ is a point along the x-axis. $y\,\!$ and $z\,\!$ are not part of the equation because the wave's magnitude and phase are the same at every point on any given y-z plane. This equation defines what that magnitude and phase are.
• $\omega \,\!$ is the wave’s angular frequency which equals $2\pi /T\,\!$, where $T\,\!$ is the period of the wave. $\omega \,\!$ has the units of radians per unit time and is a measure of how rapidly the disturbance changes over a given length of time at a particular point in space.
• $t\,\!$ is a given point in time
• $\varphi \,\!$ is the phase shift of the wave and has the units of radians. Note that a positive phase shift, at a given moment of time, shifts the wave in the negative x-axis direction. A phase shift of $2\pi \,\!$ radians shifts it exactly one wavelength.

Other formalisms which directly use the wave’s wavelength $\lambda \,\!$, period $T\,\!$, frequency $f\,\!$ and velocity $c\,\!$ are below.

$A=A_{o}cos[2\pi (x/\lambda -t/T)+\varphi ]\,\!$

$A=A_{o}cos[2\pi (x/\lambda -ft)+\varphi ]\,\!$

$A=A_{o}cos[(2\pi /\lambda )(x-ct)+\varphi ]\,\!$

To appreciate the equivalence of the above set of equations note that $f=1/T\,\!$ and $c=\lambda /T=\omega /k\,\!$

A more generalized form is used to describe a plane wave traveling in an arbitrary direction. It uses vectors in combination with the vector dot product.

$A(\mathbf {r} ,t)=A_{o}\cos(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )$

here:

• $\mathbf {k}$ is the wave vector which only differs from a wave number in that it has a direction as well as a magnitude. This means that, $|\mathbf {k} |=k=2\pi /\lambda$. The direction of the wave vector is ordinarily the direction that the plane wave is traveling, but it can differ slightly in an anisotropic medium.
• $\cdot$  is the vector dot product.
• $\mathbf {r}$ is the position vector which defines a point in three-dimensional space.

Many choose to use a more mathematically versatile formulation that utilizes the complex number plane. It requires the use of the natural exponent $e\,\!$ and the imaginary number $i\,\!$.

$U(\mathbf {r} ,t)=A_{o}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )}$

(1)

To appreciate this equation’s relationship to the earlier ones, below is this same equation expressed using sines and cosines. Observe that the first term equals the real form of the plane wave just discussed.

$U(\mathbf {r} ,t)=A_{o}\cos(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )+iA_{o}\sin(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )$

$U(\mathbf {r} ,t)=\qquad \ \ A(\mathbf {r} ,t)\qquad \qquad +iA_{o}\sin(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )$

The complex form of the plane wave just introduced can be simplified by using a complex valued amplitude $U_{o}\,\!$ in place of the real valued amplitude $A_{o}\,\!$.
Specifically, since the complex form…

$U(\mathbf {r} ,t)=A_{o}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )}$

equals

$U(\mathbf {r} ,t)=A_{o}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}e^{i\varphi }$

one can absorb the phase factor $e^{i\varphi }$ into a complex amplitude by letting $U_{o}=A_{o}e^{i\varphi }$, resulting in the more compact equation

$U(\mathbf {r} ,t)=U_{o}e^{i(\mathbf {k} \cdot \mathbf {r} -\omega t)}$

While the complex form has an imaginary component, after the necessary calculations are performed in the complex plane, its real value can be extracted giving a real valued equation representing an actual plane wave.

$Re[U(\mathbf {r} ,t)]=A(\mathbf {r} ,t)=A_{o}\cos(\mathbf {k} \cdot \mathbf {r} -\omega t+\varphi )$

The main reason one would choose to work with the complex exponential form of the plane wave is because complex exponentials are often algebraically easier to work with than the trigonometric sines and cosines. Specifically, the angle-addition rules are much simpler for complex exponentials.

Additionally, when using Fourier analysis techniques for waves in a lossy medium, the resulting attenuation is easier to deal with using complex Fourier coefficients. It should be noted however that if a wave is traveling through a lossy medium, the amplitude of the wave is no longer constant and therefore the wave is strictly speaking is no longer a true plane wave.

In quantum mechanics the solutions of the Schrödinger wave equation are by their very nature complex and in the simplest instance take a form identical to the complex plane wave representation above. The imaginary component in that instance however has not been introduced for the purpose of mathematical expediency but is in fact an inherent part of the “wave”.

User:Dave3457 : Nothing below this has been changed.