Osmotic pressure

Osmosis in a U-shaped tube.

Osmosis occurs when two solutions, containing different concentration of solute, are separated by a semipermeable membrane. Solvent molecules pass preferentially through the membrane from the low-concentration solution to the solution with higher solute concentration. The transfer of solvent molecules will continue until equilibrium is attained.

In order to visualize this effect, imagine a U-shaped tube with equal amounts of water on both sides of a membrane which is permeable to water and which is impermeable to sugar molecules. Dialysis tubing is an example of a material which can act as a semi-permeable membrane. When sugar is added to the water in one arm, the height of the liquid column on that side will then rise and that on the other side will drop. This process will continue until the osmotic pressures of the water and sugar solution are equal. Osmotic pressure can then be obtained from a measurementof the difference in height between the liquids in the two arms.

Theory and measurement

A Pfeffer cell used for early measurements of osmotic pressure

Jacobus van 't Hoff found a quantitative relationship between osmotic pressure and solute concentration, expressed in the following equation.

$\Pi =iCRT$

where $\Pi$ is osmotic pressure, i is the dimensionless van 't Hoff index, C is the molar concentration of solute, R is the ideal gas constant, and T is the temperature in kelvins. This formula applies when the solute concentration is sufficiently low that the solution can be treated as an ideal solution. The proportionality to concentration means that osmotic pressure is a colligative property. Note the similarity of this formula to the ideal gas law in the form $p={n \over V}RT=c_{\text{gas}}RT$ where n is the total number of moles of gas molecules in the volume V, and n/V is the molar concentration of gas molecules. Harmon Northrop Morse and Frazer showed that the equation applied to more concentrated solutions if the unit of concentration was molal rather than molar.

For more concentrated solutions the van 't Hoff equation can be extended as a power series in solute concentration, C. To a first approximation,

$\Pi =\Pi _{0}+AC^{2}$

where $\Pi _{0}$ is the ideal pressure and A is an empirical parameter. The value of the parameter A (and of parameters from higher-order approximations) can be used to calculate Pitzer parameters. Empirical parameters are used to quantify the behaviour of solutions of ionic and non-ionic solutes which are not ideal solutions in the thermodynamic sense.

The Pfeffer cell was developed for the measurement of osmotic pressure.

Applications

Osmotic pressure on red blood cells

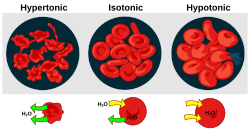
Osmotic pressure measurement may be used for the determination of molecular weights.

Osmotic pressure is an important factor affecting cells. Osmoregulation is the homeostasis mechanism of an organism to reach balance in osmotic pressure.

• Hypertonicity is the presence of a solution that causes cells to shrink.
• Hypotonicity is the presence of a solution that causes cells to swell.
• Isotonicity is the presence of a solution that produces no change in cell volume.

When a biological cell is in a hypotonic environment, the cell interior accumulates water, water flows across the cell membrane into the cell, causing it to expand. In plant cells, the cell wall restricts the expansion, resulting in pressure on the cell wall from within called turgor pressure. Turgor pressure allows herbaceous plants to stand upright. It is also the determining factor for how plants regulate the aperture of their stomata. In animal cells excessive osmotic pressure can result in cytolysis.

Osmotic pressure is the basis of filtering ("reverse osmosis"), a process commonly used in water purification. The water to be purified is placed in a chamber and put under an amount of pressure greater than the osmotic pressure exerted by the water and the solutes dissolved in it. Part of the chamber opens to a differentially permeable membrane that lets water molecules through, but not the solute particles. The osmotic pressure of ocean water is about 27 atm. Reverse osmosis desalinates fresh water from ocean salt water.

Derivation of the van 't Hoff formula

Consider the system at the point when it has reached equilibrium. The condition for this is that the chemical potential of the solvent (since only it is free to flow toward equilibrium) on both sides of the membrane is equal. The compartment containing the pure solvent has a chemical potential of $\mu ^{0}(p)$, where $p$ is the pressure. On the other side, in the compartment containing the solute, the chemical potential of the solvent depends on the mole fraction of the solvent, $0<x_{v}<1$. Besides, this compartment can assume a different pressure, $p'$. We can therefore write the chemical potential of the solvent as $\mu _{v}(x_{v},p')$. If we write $p'=p+\Pi$, the balance of the chemical potential is therefore:

$\mu _{v}^{0}(p)=\mu _{v}(x_{v},p+\Pi )$.

Here, the difference in pressure of the two compartments $\Pi \equiv p'-p$ is defined as the osmotic pressure exerted by the solutes. Holding the pressure, the addition of solute decreases the chemical potential (an entropic effect). Thus, the pressure of the solution has to be increased in an effort to compensate the loss of the chemical potential.

In order to find $\Pi$, the osmotic pressure, we consider equilibrium between a solution containing solute and pure water.

$\mu _{v}(x_{v},p+\Pi )=\mu _{v}^{0}(p)$.

We can write the left hand side as:

$\mu _{v}(x_{v},p+\Pi )=\mu _{v}^{0}(p+\Pi )+RT\ln(\gamma _{v}x_{v})$,

where $\gamma _{v}$ is the activity coefficient of the solvent. The product $\gamma _{v}x_{v}$ is also known as the activity of the solvent, which for water is the water activity $a_{w}$. The addition to the pressure is expressed through the expression for the energy of expansion:

$\mu _{v}^{o}(p+\Pi )=\mu _{v}^{0}(p)+\int _{p}^{p+\Pi }\!V(p')\,\mathrm {d} p'$,

where $V$ is the molar volume (m³/mol). Inserting the expression presented above into the chemical potential equation for the entire system and rearranging will arrive at:

$-RT\ln(\gamma _{v}x_{v})=\int _{p}^{p+\Pi }\!V(p')\,\mathrm {d} p'$.

If the liquid is incompressible the molar volume is constant, $V(p')\equiv V$, and the integral becomes $\Pi V$. Thus, we get

$\Pi =-(RT/V)\ln(\gamma _{v}x_{v})$.

The activity coefficient is a function of concentration and temperature, but in the case of dilute mixtures, it is often very close to 1.0, so

$\Pi =-(RT/V)\ln(x_{v})$.

For aqueous solutions of salts, ionisation must be taken into account. For example, 1 mole of NaCl ionises to 2 moles of ions.

See also

• Gibbs–Donnan effect

External links

• What is Osmosis? Explanation and Understanding of a Physical Phenomenon