Projective space: Difference between revisions

Content deleted Content added

Inline

Revision as of 07:22, 5 August 2019

In graphical perspective, parallel lines in the plane intersect in a vanishing point on the horizon.

In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seems to meet at infinity. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines.

This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, point and lines are primitive entities the are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to at the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from the following definition, which is more often encountered in modern textbooks.

Using linear algebra, a projective space of dimension $n$ is defined as the set of the vector lines (that is, vector subspaces of dimension one) in a vector space $V$ of dimension $n + 1$ . Equivalently, it is the quotient set of $V \ {0}$ by the equivalence relation "being on the same vector line". As a vector line intersects the unit sphere of $V$ in two antipodal points, projective spaces can be equivalently defined as spheres in which antipodal points are identified. A projective space of dimension 1 is a projective line, and a projective space of dimension 2 is a projective plane.

Projective spaces are widely used in geometry, as allowing simpler statements and simpler proofs. For example, in affine geometry, two distinct lines in a plane intersect in at most one point, while, in projective geometry, they intersect in exactly one point. Also, there is only one class of conic sections, which can be distinguished only by their intersections with the line at infinity: two intersection points for hyperbolas; one for the parabola, which is tangent to the line at infinity; and no real intersection point of ellipses.

In topology, and more specifically in manifold theory, projective spaces play a fundamental role, being typical examples of non-orientable manifolds.

Motivation

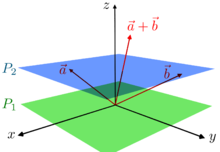
As outlined above, projective spaces were introduced for formalizing statements like "two coplanar lines intersect in exactly one point, and this point is at infinity if the lines are parallel." Such statements are suggested by the study of perspective, which may be considered as a central projection of the three dimensional space onto a plane (see Pinhole camera model). More precisely, the entrance pupil of a camera or of the eye of an observer is the center of projection, and the image is formed on the projection plane.

Mathematically, the center of projection is a point $O$ of the space (the intersection of the axes in the figure); the projection plane ( $P 2$ , in blue on the figure) is a plane not passing through $O$ , which is often chosen to be the plane of equation $z = 1$ , when Cartesian coordinates are considered. Then, the central projection maps a point $P$ to the intersection of the line $OP$ with the projection plane. Such an intersection exists if and only if the point $P$ does not belong to the plane ( $P 1$ , in green on the figure) that passes through $O$ and is parallel to $P 2$ .

It follows that the lines passing through $O$ split in two disjoint subsets: the lines that are not contained in $P 1$ , which are in one to one correspondence with the points of $P 2$ , and those contained in $P 1$ , which are in one to one correspondence with the directions of parallel lines in $P 2$ . This suggests to define the points (called here projective points for clarity) of the projective plane as the lines passing through $O$ . A projective line in this plane consists of all projective points (which are lines) contained in a plane passing through $O$ . As the intersection of two planes passing through $O$ is a line passing through $O$ , the intersection of two distinct projective lines consists of a single projective point. The plane $P 1$ defines a projective line which is called the line at infinity of $P 2$ . By identifying each point of $P 2$ with the corresponding projective point, one can thus say that the projective plane is the disjoint union of $P 2$ and the (projective) line at infinity.

As an affine space with a distinguished point $O$ may be identified with its associated vector space (see Affine space § Vector spaces as affine spaces), the preceding construction is generally done by starting from a vector space and is called projectivization. Also, the construction can be done by starting with a vector space of any positive dimension.

So, a projective space of dimension $n$ can be defined as the set of vector lines (vector subspaces of dimension one) in a vector space of dimension $n + 1$ . A projective space can also be defined as the elements of any set that is in natural correspondence with this set of vector lines.

This set can be the set of equivalence classes under the equivalence relation between vectors defined by "one vector is the product of the other by a nonzero scalar". In other words, this amounts to define a projective space as the set of vector lines in which the zero vector has been removed.

A third equivalent definition is to define a projective space of dimension $n$ as the set of pairs of antipodal points in a sphere of dimension $n$ (in a space of dimension $n + 1$ .

Definition

Given a vector space $V$ over a field $K$ , the projective space $P (V)$ is the set of equivalence classes of $V \ {0}$ under the equivalence relation $~$ defined by $x ~ y$ if there is a nonzero element $λ$ of $K$ such that $x = λy$ . If $V$ is a topological vector space, the quotient space $P (V)$ is a topological space, endowed with the quotient topology. This is the case when $K$ ie the field $\mathbb {R}$ of the real numbers or the field $\mathbb {C}$ of the complex numbers. If $V$ is finite dimensional, the dimension of $P (V)$ is the dimension of $V$ minus one.

In the common case where $V = K n + 1$ , the projective space $P (V)$ is denoted $P n (K)$ (or $P n (K)$ , although this notation may be confused with exponentiation). The space $P n (K)$ is often called the projective space of dimension $n$ over $K$ , or the projective $n$ -space, since all projective spaces of dimension $n$ are isomorphic to it (because every $K$ vector space of dimension $n + 1$ is isomorphic to $K n + 1$ .

The elements of a projective space $P (V)$ are commonly called points. If a basis of $V$ has been chosen, and, in particular if $V = K n + 1$ , the projective coordinates of a point P are the coordinates on the basis of any element of the corresponding equivalence class. These coordinates are commonly denoted $[x 0 : ... : x n]$ , the colons and the brackets being used for distinguishing from usual coordinates, and emphasizing that this is an equivalence class, which is defined up to the multiplication by a non zero constant. That is, if $[x 0 : ... : x n]$ are projective coordinates of a point, then $[λx 0 : ... : λx n]$ are also projective coordinates of the same point, for any nonzero $λ$ in $K$ . Also, the above definition implies that $[x 0 : ... : x n]$ are projective coordinates of a point if and only if at least one of the coordinates is nonzero.

If $K$ is the field of real or complex number, a projective space is called a real projective space or a complex projective space, respectively. If $n$ is one or two, a projective space of dimension $n$ is called a projective line or a projective plane, respectively. The complex projective line is also called the Riemann sphere.

All these definitions extend naturally to the case where $K$ is a division ring; see, for example, Quaternionic projective space. The notation $PG(n, K)$ is sometimes used for $P n (K)$ .^[1] If $K$ is a finite field with $q$ elements, $P n (K)$ is often denoted $PG(n, q)$ (see PG(3, 2)).

Projective space as a manifold

The above definition of projective space gives a set. For purposes of differential geometry, which deals with manifolds, it is useful to endow this set with a (real or complex) manifold structure.

Namely, identifying a point of the projective space with its homogeneous coordinates, consider the following subsets of the projective space:

U_{i}=\{[x_{0}:\cdots :x_{n}],x_{i}\neq 0\},\quad i=0,\dots ,n.

By the definition of projective space, their union is the whole projective space. Furthermore, U_i is in bijection with Rⁿ (or Cⁿ) via the following maps:

[x_{0}:\cdots :x_{n}]\mapsto \left({\frac {x_{0}}{x_{i}}},\dots ,{\widehat {\frac {x_{i}}{x_{i}}}},\dots ,{\frac {x_{n}}{x_{i}}}\right)

[y_{0}:\cdots :y_{i-1}:1:y_{i+1}:\cdots :y_{n}]\leftarrow \left(y_{0},\dots ,{\widehat {y_{i}}},\dots y_{n}\right)

(the hat means that the i-th entry is missing).

The example image shows P¹(R). (Antipodal points are identified in P¹(R), though). It is covered by two copies of the real line R, each of which covers the projective line except one point, which is "the" (or "a") point at infinity.

We first define a topology on projective space by declaring that these maps shall be homeomorphisms, that is, a subset of U_i is open iff its image under the above isomorphism is an open subset (in the usual sense) of Rⁿ. An arbitrary subset A of Pⁿ(R) is open if all intersections A ∩ U_i are open. This defines a topological space.

The manifold structure is given by the above maps, too.

Another way to think about the projective line is the following: take two copies of the affine line with coordinates x and y, respectively, and glue them together along the subsets x ≠ 0 and y ≠ 0 via the maps

x\mapsto {\frac {1}{x}},\,y\mapsto {\frac {1}{y}}.

The resulting manifold is the projective line. The charts given by this construction are the same as the ones above. Similar presentations exist for higher-dimensional projective spaces.

The above decomposition in disjoint subsets reads in this generality:

\cdots

,

this so-called cell-decomposition can be used to calculate the singular cohomology of projective space.

All of the above holds for complex projective space, too. The complex projective line P¹(C) is an example of a Riemann surface.

Projective spaces in algebraic geometry

The covering by the above open subsets also shows that projective space is an algebraic variety (or scheme); it is covered by n + 1 affine n-spaces. The construction of a projective scheme is an instance of the Proj construction.

Projective spaces in algebraic topology

Real projective n-space has a quite straightforward CW complex structure where Pⁿ(R) is obtained from Pⁿ⁻¹(R) by attaching an n-cell with the quotient projection Sⁿ⁻¹ → Pⁿ⁻¹(R) as the attaching map.

Projective space and affine space

There are some advantages of the projective space compared with affine space (e.g., Pⁿ(R) vs. Aⁿ(R)). For these reasons it is important to know when a given manifold or variety is projective, i.e., embeds into (is a closed subset of) projective space. (Very) ample line bundles are designed to tackle this question.

Note that a projective space can be formed by the projectivization of a vector space, as lines through the origin, but cannot be formed from an affine space without a choice of basepoint. That is, affine spaces are open subspaces of projective spaces, which are quotients of vector spaces.

Projective space is a compact topological space, affine space is not. Therefore, Liouville's theorem applies to show that every holomorphic function on Pⁿ(C) is constant. Another consequence is, for example, that integration of functions or differential forms on Pⁿ does not cause convergence issues.
On a projective complex manifold X, cohomology groups of coherent sheaves are finitely generated. (The above example is H⁰(Pⁿ(C), O), the zeroth cohomology of the sheaf of holomorphic functions O). In the parlance of algebraic geometry, projective space is proper. The above results hold in this context, too.
For complex projective space, every complex submanifold X ⊂ Pⁿ(C) (i.e., a manifold cut out by holomorphic equations) is necessarily an algebraic variety (i.e., given by polynomial equations). This is Chow's theorem, it allows the direct use of algebraic–geometric methods for these ad hoc analytically defined objects.
As outlined above, lines in P² or more generally hyperplanes in Pⁿ always do intersect. This extends to non-linear objects, as well: appropriately defining the degree of an algebraic curve, which is roughly the degree of the polynomials needed to define the curve (see Hilbert polynomial), it is true (over an algebraically closed field k) that any two projective curves C₁, C₂ ⊂ Pⁿ(k) of degree e and f intersect in exactly ef points, counting them with multiplicities (see Bézout's theorem). This is applied, for example, in defining a group structure on the points of an elliptic curve, like y² = x³ − x + 1. The degree of an elliptic curve is 3. Consider the line x = 1, which intersects the curve (inside affine space) exactly twice, namely in (1, 1) and (1, −1). However, inside P², the projective closure of the curve is given by the homogeneous equation
$\qquad y^{2}z=x^{3}-xz^{2}+z^{3},$
which intersects the line (given inside P² by x = z) in three points: [1: 1: 1], [1: −1: 1] (corresponding to the two points mentioned above), and [0: 1: 0].
Any projective group variety, i.e., a projective variety, whose points form an abstract group, is necessarily an abelian variety. Elliptic curves are examples for abelian varieties. The commutativity fails for non-projective group varieties, as the example GL_n(k) (the general linear group) shows.

Axioms for projective space

A projective space S can be defined axiomatically as a set P (the set of points), together with a set L of subsets of P (the set of lines), satisfying these axioms:^[2]

Each two distinct points p and q are in exactly one line.
Veblen's axiom:^[3] If a, b, c, d are distinct points and the lines through ab and cd meet, then so do the lines through ac and bd.
Any line has at least 3 points on it.

The last axiom eliminates reducible cases that can be written as a disjoint union of projective spaces together with 2-point lines joining any two points in distinct projective spaces. More abstractly, it can be defined as an incidence structure (P, L, I) consisting of a set P of points, a set L of lines, and an incidence relation I that states which points lie on which lines.

The structures defined by these axioms are more general than those obtained from the vector space construction given above. If the (projective) dimension is at least three then, by the Veblen–Young theorem, there is no difference. However, for dimension two, there are examples that satisfy these axioms that can not be constructed from vector spaces (or even modules over division rings). These examples do not satisfy the Theorem of Desargues and are known as Non-Desarguesian planes. In dimension one, any set with at least three elements satisfies the axioms, so it is usual to assume additional structure for projective lines defined axiomatically.^[4]

It is possible to avoid the troublesome cases in low dimensions by adding or modifying axioms that define a projective space. Coxeter (1969, p. 231) gives such an extension due to Bachmann.^[5] To ensure that the dimension is at least two, replace the three point per line axiom above by;

There exist four points, no three of which are collinear.

To avoid the non-Desarguesian planes, include Pappus's theorem as an axiom;^[6]

If the six vertices of a hexagon lie alternately on two lines, the three points of intersection of pairs of opposite sides are collinear.

And, to ensure that the vector space is defined over a field that does not have even characteristic include Fano's axiom;^[7]

The three diagonal points of a complete quadrangle are never collinear.

A subspace of the projective space is a subset X, such that any line containing two points of X is a subset of X (that is, completely contained in X). The full space and the empty space are always subspaces.

The geometric dimension of the space is said to be n if that is the largest number for which there is a strictly ascending chain of subspaces of this form:

\varnothing =X_{-1}\subset X_{0}\subset \cdots X_{n}=P.

A subspace $X_{i}$ in such a chain is said to have (geometric) dimension $i$ . Subspaces of dimension 0 are called points, those of dimension 1 are called lines and so on. If the full space has dimension $n$ then any subspace of dimension $n-1$ is called a hyperplane.

Classification

Dimension 0 (no lines): The space is a single point.
Dimension 1 (exactly one line): All points lie on the unique line.
Dimension 2: There are at least 2 lines, and any two lines meet. A projective space for n = 2 is equivalent to a projective plane. These are much harder to classify, as not all of them are isomorphic with a PG(d, K). The Desarguesian planes (those that are isomorphic with a PG(2, K)) satisfy Desargues's theorem and are projective planes over division rings, but there are many non-Desarguesian planes.
Dimension at least 3: Two non-intersecting lines exist. Veblen & Young (1965) proved the Veblen–Young theorem that every projective space of dimension n ≥ 3 is isomorphic with a PG(n, K), the n-dimensional projective space over some division ring K.

Finite projective spaces and planes

A finite projective space is a projective space where P is a finite set of points. In any finite projective space, each line contains the same number of points and the order of the space is defined as one less than this common number. For finite projective spaces of dimension at least three, Wedderburn's theorem implies that the division ring over which the projective space is defined must be a finite field, GF(q), whose order (that is, number of elements) is q (a prime power). A finite projective space defined over such a finite field has q + 1 points on a line, so the two concepts of order coincide. Notationally, PG(n, GF(q)) is usually written as PG(n, q).

All finite fields of the same order are isomorphic, so, up to isomorphism, there is only one finite projective space for each dimension greater than or equal to three, over a given finite field. However, in dimension two there are non-Desarguesian planes. Up to isomorphism there are

1, 1, 1, 1, 0, 1, 1, 4, 0, … (sequence A001231 in the OEIS)

finite projective planes of orders 2, 3, 4, ..., 10, respectively. The numbers beyond this are very difficult to calculate and are not determined except for some zero values due to the Bruck–Ryser theorem.

The smallest projective plane is the Fano plane, PG(2, 2) with 7 points and 7 lines. The smallest 3-dimensional projective spaces is PG(3,2), with 15 points, 35 lines and 15 planes.

Morphisms

Injective linear maps T ∈ L(V, W) between two vector spaces V and W over the same field k induce mappings of the corresponding projective spaces P(V) → P(W) via:

[v] → [T(v)],

where v is a non-zero element of V and [...] denotes the equivalence classes of a vector under the defining identification of the respective projective spaces. Since members of the equivalence class differ by a scalar factor, and linear maps preserve scalar factors, this induced map is well-defined. (If T is not injective, it has a null space larger than {0}; in this case the meaning of the class of T(v) is problematic if v is non-zero and in the null space. In this case one obtains a so-called rational map, see also birational geometry).

Two linear maps S and T in L(V, W) induce the same map between P(V) and P(W) if and only if they differ by a scalar multiple, that is if T = λS for some λ ≠ 0. Thus if one identifies the scalar multiples of the identity map with the underlying field K, the set of K-linear morphisms from P(V) to P(W) is simply P(L(V, W)).

The automorphisms P(V) → P(V) can be described more concretely. (We deal only with automorphisms preserving the base field K). Using the notion of sheaves generated by global sections, it can be shown that any algebraic (not necessarily linear) automorphism must be linear, i.e., coming from a (linear) automorphism of the vector space V. The latter form the group GL(V). By identifying maps that differ by a scalar, one concludes that

Aut(P(V)) = Aut(V)/K^× = GL(V)/K^× =: PGL(V),

the quotient group of GL(V) modulo the matrices that are scalar multiples of the identity. (These matrices form the center of Aut(V).) The groups PGL are called projective linear groups. The automorphisms of the complex projective line P¹(C) are called Möbius transformations.

Dual projective space

When the construction above is applied to the dual space V^∗ rather than V, one obtains the dual projective space, which can be canonically identified with the space of hyperplanes through the origin of V. That is, if V is n dimensional, then P(V^∗) is the Grassmannian of n − 1 planes in V.

In algebraic geometry, this construction allows for greater flexibility in the construction of projective bundles. One would like to be able associate a projective space to every quasi-coherent sheaf E over a scheme Y, not just the locally free ones.^{[clarification needed]} See EGA_II, Chap. II, par. 4 for more details.

Generalizations

dimension: The projective space, being the "space" of all one-dimensional linear subspaces of a given vector space V is generalized to Grassmannian manifold, which is parametrizing higher-dimensional subspaces (of some fixed dimension) of V.
sequence of subspaces: More generally flag manifold is the space of flags, i.e., chains of linear subspaces of V.
other subvarieties: Even more generally, moduli spaces parametrize objects such as elliptic curves of a given kind.
other rings: Generalizing to associative rings (rather than only fields) yields, for example, the projective line over a ring.
patching: Patching projective spaces together yields projective space bundles.

Severi–Brauer varieties are algebraic varieties over a field k, which become isomorphic to projective spaces after an extension of the base field k.

Another generalization of projective spaces are weighted projective spaces; these are themselves special cases of toric varieties.^[8]

Notes

^ Mauro Biliotti, Vikram Jha, Norman L. Johnson (2001) Foundations of Translation Planes, p. 506, Marcel Dekker ISBN 0-8247-0609-9
^ Beutelspacher & Rosenbaum 1998, pgs. 6–7
^ also referred to as the Veblen–Young axiom and mistakenly as the axiom of Pasch (Beutelspacher & Rosenbaum 1998, pgs. 6–7). Pasch was concerned with real projective space and was attempting to introduce order, which is not a concern of the Veblen–Young axiom.
^ Baer 2005, p. 71
^ Bachmann, F. (1959), Aufbau der Geometrie aus dem Spiegelsbegriff, Grundlehren der mathematischen Wissenschaftern, 96, Berlin: Springer, pp. 76–77
^ As Pappus's theorem implies Desargues's theorem this eliminates the non-Desarguesian planes and also implies that the space is defined over a field (and not a division ring).
^ This restriction allows the real and complex fields to be used (zero characteristic) but removes the Fano plane and other planes that exhibit atypical behavior.
^ Mukai 2003, example 3.72

References

Afanas'ev, V.V. (2001) [1994], "projective space", Encyclopedia of Mathematics, EMS Press
Baer, Reinhold (2005) [first published 1952], Linear Algebra and Projective Geometry, Dover, ISBN 978-0-486-44565-6
Beutelspacher, Albrecht; Rosenbaum, Ute (1998), Projective geometry: from foundations to applications, Cambridge University Press, ISBN 978-0-521-48277-6, MR 1629468
Coxeter, Harold Scott MacDonald (1974), Introduction to Geometry, New York: John Wiley & Sons, ISBN 0-471-18283-4
Coxeter, Harold Scott MacDonald (1969), Projective geometry, Toronto, Ont.: University of Toronto Press, ISBN 0-8020-2104-2, MR 0346652, OCLC 977732
Dembowski, P. (1968), Finite geometries, Ergebnisse der Mathematik und ihrer Grenzgebiete, Band 44, Berlin, New York: Springer-Verlag, ISBN 3-540-61786-8, MR 0233275
Greenberg, M.J.; Euclidean and non-Euclidean geometries, 2nd ed. Freeman (1980).
Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157, esp. chapters I.2, I.7, II.5, and II.7
Hilbert, D. and Cohn-Vossen, S.; Geometry and the imagination, 2nd ed. Chelsea (1999).
Mukai, Shigeru (2003), An Introduction to Invariants and Moduli, Cambridge Studies in Advanced Mathematics, Cambridge University Press, ISBN 978-0-521-80906-1
Veblen, Oswald; Young, John Wesley (1965), Projective geometry. Vols. 1, 2, Blaisdell Publishing Co. Ginn and Co. New York-Toronto-London, MR 0179666 (Reprint of 1910 edition)

External links

[1] Mauro Biliotti, Vikram Jha, Norman L. Johnson (2001) Foundations of Translation Planes, p. 506, Marcel Dekker ISBN 0-8247-0609-9

[2] Beutelspacher & Rosenbaum 1998, pgs. 6–7

[3] so referred to as the Veblen–Young axiom and mistakenly as the axiom of Pasch (Beutelspacher & Rosenbaum 1998, pgs. 6–7). Pasch was concerned with real projective space and was attempting to introduce order, which is not a concern of the Veblen–Young axiom.

[4] Baer 2005, p. 71

[5] Bachmann, F. (1959), Aufbau der Geometrie aus dem Spiegelsbegriff, Grundlehren der mathematischen Wissenschaftern, 96, Berlin: Springer, pp. 76–77

[6] As Pappus's theorem implies Desargues's theorem this eliminates the non-Desarguesian planes and also implies that the space is defined over a field (and not a division ring).

[7] This restriction allows the real and complex fields to be used (zero characteristic) but removes the Fano plane and other planes that exhibit atypical behavior.

[8] Mukai 2003, example 3.72

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

@@ Line 37: / Line 37: @@
 If {{mvar|K}} is the field of real or complex number, a projective space is called a [[real projective space]] or a [[complex projective space]], respectively. If {{math|''n''}} is one or two, a projective space of dimension {{math|''n''}} is called a [[projective line]] or a [[projective plane]], respectively. The complex projective line is also called the [[Riemann sphere]].
-All these definitions extend naturally to the case where {{mvar|K}} is a [[division ring]]; see, for example, [[Quaternionic projective space]]. The notation {{math|PG(''n'', ''K'')}} is sometimes used for {{math|'''P'''{{sub|''n''}}(''K'')}}.<ref>Mauro Biliotti, Vikram Jha, Norman L. Johnson (2001) ''Foundations of Translation Planes'', p.&nbsp;506, [[Marcel Dekker]] {{isbn|0-8247-0609-9}}</ref> If {{mvar|K}} is a [[finite field]] with {{mvar|q}} elements, {{math|'''P'''{{sub|''n''}}(''K'')}} is often denoted {{math|PG(''n'', ''q'')}} (see [[PG(3,2)]]).
+All these definitions extend naturally to the case where {{mvar|K}} is a [[division ring]]; see, for example, [[Quaternionic projective space]]. The notation {{math|PG(''n'', ''K'')}} is sometimes used for {{math|'''P'''{{sub|''n''}}(''K'')}}.<ref>Mauro Biliotti, Vikram Jha, Norman L. Johnson (2001) ''Foundations of Translation Planes'', p.&nbsp;506, [[Marcel Dekker]] {{isbn|0-8247-0609-9}}</ref> If {{mvar|K}} is a [[finite field]] with {{mvar|q}} elements, {{math|'''P'''{{sub|''n''}}(''K'')}} is often denoted {{math|PG(''n'', ''q'')}} (see [[PG(3, 2)]]).
 ==Projective space as a manifold==

v t e Dimension
Dimensional spaces	Vector space Euclidean space Affine space Projective space Free module Manifold Algebraic variety Spacetime
Other dimensions	Krull Lebesgue covering Inductive Hausdorff Minkowski Fractal Degrees of freedom
Polytopes and shapes	Hyperplane Hypersurface Hypercube Hyperrectangle Demihypercube Hypersphere Cross-polytope Simplex Hyperpyramid
Dimensions by number	Zero One Two Three Four Five Six Seven Eight n-dimensions
See also	Hyperspace Codimension
Category

Revision as of 07:22, 5 August 2019

Motivation

Definition

Projective space as a manifold

Projective spaces in algebraic geometry

Projective spaces in algebraic topology

Projective space and affine space

Axioms for projective space

Classification

Finite projective spaces and planes

Morphisms

Dual projective space

Generalizations

See also

Generalizations

Projective geometry

Related

Notes

References

External links