Penrose tiling

A Penrose tiling

A Penrose tiling is an aperiodic tiling of the plane discovered by Roger Penrose in 1973 . Being aperiodic, it has no translational symmetry - it never repeats itself exactly, but nevertheless it has a fivefold rotational symmetry. The Penrose tiling is also a prime example of a quasicrystal as it produces a sharply outlined diffractogram. There are two popular variants of the Penrose tiling which use different sets of tiles. Robert Ammann independently discovered the tiling. A similarity with some decorative patterns used in the Middle East has been frequently noted and in February 2007 a paper by Steinhardt and Lu offered evidence that a Penrose tiling underlies some examples of medieval Islamic art. Roger Penrose acknowledges inspiration from the work of Johannes Kepler.

In 1982 Dan Shechtman reported that a sample of aluminium-manganese alloy produced a sharp diffractogram with fivefold symmetry. At that time it was assumed that such symmetry is incompatible with the ability to diffract. The combination of these two features is possible only in an aperiodic structure. The full three-dimensional arrangement, which exhibits icosahedral symmetry, had been worked out by Robert Ammann. The atoms in the planes corresponding to the unusual symmetry are arranged in the pattern of a Penrose tiling. De Bruijn has shown that it was possible to obtain the Penrose tiling as a projection from a five-dimensional cubic lattice, which explains its crystal-like ability to diffract. The Penrose Tiling has become the most studied - and most popular - quasicrystal. The physicists' interest led to an other approach which connected the Penrose tiling to extremal problems and proved it to be a model for the state with minimum energy in some systems. This development came after Petra Gummelt's demonstration that it is possible to build an aperiodic tiling with a single decagonal tile if overlapping is allowed and this construction reproduced the Penrose tiling .

Construction principles

Hao Wang proved that it must be possible to tile the plane aperiodically and shortly after Robert Berger proposed the first set of 20426 distinct tile shapes which plane completely only in an aperiodic pattern. The set was rapidly reduced, reaching the number of two. The rules which produce aperiodicity may be embodied in dents, arrows or colors on the edges of the tiles. Using plain geometric forms is also possible but the invisible rules are still observed (to avoid trivial tilings). The Penrose tiling, as it was discovered, uses two triangles glued together to form a pair of rhombuses or a pair of shapes known as a kite and a dart. With these two sets an equivalent tiling is produced. The basic triangles are also known as Robinson triangles which have been used to produce aperiodic tilings by substitutions.

Rhombus tiling

The Penrose rhombuses have equal sides and angles which are multiples of one tenth of a circle (36 degrees).

• The first tile, known as the thick rhombus T, has four corners with the angles {72, 108, 72, 108} degrees.
• The second tile is the thin rhombus t with angles of {36, 144, 36, 144} degrees.

There are 23 sets of angles which would add up to 360 degrees at a vertex and most of them admit different orderings, but the rules of the tiling allow only 7 distinct types of vertexes. The two tiles appear in the tiling with equal constant frequencies in just ten different orientations and the tiling has a statistical tenfold symmetry . There are many local fivefold centers and a unique center point of global fivefold symmetry where five mirror lines cross. As the tiling is aperiodic, there is no translational symmetry: the pattern never repeats exactly. However, given a bounded region, no matter how large, that region will be repeated an infinite number of times within the tiling.

File:Penrhombus.jpg

Matching rules and substitutions for the Penrose Tiling

The tiles are put together with one general rule: no two tiles can be touching so as to form a single parallelogram. Given this rule, there is an uncountably infinite combination of ways to tile the plane without gaps. It is easy to check that some of the compact patches consisting of three tiles admit two different arrangements within the same perimeter and thus variations are possible. Cataloging the patches of finite size allows to sort the different rhombus tilings into classes of local isomorphism. The original Penrose tiling is specified more simply by its rules for substitutions or matching.

A variant of the Penrose Tiling which is not a quasicrystal

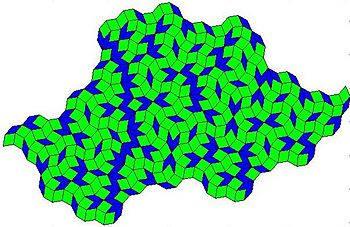
The picture shows a variant rhombus tiling, built with the same Penrose tiles, used in the same proportion. The underlying symmetry is also fivefold but this tiling is not a quasicrystal. It can be obtained either by 'decorating' the rhombuses of the original tiling with smaller ones or directly by the substitutions T->3T+t, t->T+2t, but not by de Bruijn's cut-and-project method .

Drawing the Penrose tiling

L-System approach

The Penrose tiling can be drawn using the following L-system:

variables:	1 6 7 8 9 [ ]
constants:	+ −;
start:	[7]++[7]++[7]++[7]++[7]
rules:	6 → 81++91−−−−71[−81−−−−61]++
	7 → +81−−91[−−−61−−71]+
	8 → −61++71[+++81++91]−
	9 → −−81++++61[+91++++71]−−71
	1 → (eliminated at each iteration)
angle:	36º

Where, 1 means "draw forward", + means "turn left by angle", and − means "turn right by angle" (see turtle graphics). The [ means save the present position and direction to restore them when corresponding ] is executed. The symbols 6, 7, 8 and 9 do not correspond to any action; they are there only to produce the correct curve evolution.

Evolution of L-system for n=1, n=2, n=3

Deflation approach

The penrose tiling can also be generated by a deflation algorithm, which relies on the matching rule.

Matching rule

In order to enforce the parallelogram rule, one can draw a pattern on the two types of tiles that occur in the penrose tiling. In the examples below, the two tiles are the so-called 'Kite' and 'Dart' which are alternatives for the two rhombs in the introduction.

The green and the red arcs in the tiles indicate how the tiles should be connected: When two tiles share an edge in a tiling, the patterns must match at these edges.

Deflation

Based on the matching rule, one can define a recursive substitution (i.e. deflation) that yields the penrose tiling. The algorithm starts with an axiom. This is an initial finite part of the penrose tiling that obeys the matching rules. An axiom can be as simple a single tile. Consequently, the deflation is a process that consists of several generations. During one generation, each tile is systematically substituted by one or more new tiles that exactly cover the area of the original tile. A set of substitution rules is only valid if the pattern on each tile after substitution results in equivalent matching conditions.

An example of such substitution rules is given in the table below. The tiles are half darts and half kites.

	Half a kite	Half a dart
Generation i
Generation i+1

Examples

These are four examples of penrose tilings generated with the deflation approach.

Name	Generation 0 (or axiom)	Generation 1	Generation 2	Generation 3
Kite (half)
Dart (half)
Sun
Star

Decagonal covering

In 1996 German mathematician Petra Gummelt demonstrated that the Penrose tiling can be built with a single decagonal tile if two kinds of overlap are allowed. This novel approach has been called 'covering', as 'tiling' is usually taken to mean 'without overlapping'. The decagonal tile is decorated with colored patches and the covering rule allows only the overlap of these decorations.

File:Gummelts.png

Gummelt's decagon and the two kinds of overlap

Decomposing the decagonal tile into kites and darts transform the aperiodic covering into a Penrose tiling. If a fat 'T' rhombus is inscribed into each decagon, that part of the Penrose tiling corresponding to these shapes is obtained, while places for thin tiles are left unoccupied. The covering method is taken to be a realistic model for the growth of quasicrystals. Different atomic clusters 'share' the fragments from which the aperiodic structure is built. The analogy with crystals constructed from a unit cell is restored when the overlapping decagons are seen as quasi-unit cells.

Fibonacci and Golden Ratio features

The Penrose Tiling, the Fibonacci sequence and the Golden ratio are intricately related and perhaps they should be considered as different aspects of the same phenomenon.

• the ratio of thick $T$ to thin $t$ rhombuses in the infinite tile is the golden ratio $T$/$t$ = φ = 1.618..
• the Conway worms, sequences of neighbouring rhombuses with parallel sides, are Fibonacci ordered appearances of $T$ and $t$ and thus the Ammann bars also form Fibonacci ordered grids
• around each $5T-$ star a segmented Fibonacci spiral is formed by the sides of rhombuses [1]
• the distances between repeated finite motifs in the tiling grow as Fibonacci numbers when the size of the motif increases
• the substitution scheme $T->2T+t,t->T+t$ uses φ as a scaling factor; implemented as a symbol sequence ( e.g. 1->101, 0->10) this substitution produces a series of words with lengths which are the Fibonacci numbers with odd index, F(2n+1) for n=1,2,3.., the limit being the infinite Fibonacci binary sequence
• the eigenvalues of the substitution matrix are φ+1 and 2-φ

Trivia

Pentaplex Ltd., a company in Yorkshire, England controlled by Penrose, owns the licensing rights to Penrose tilings . Penrose and Pentaplex filed a lawsuit against Kimberly-Clark for breach of copyright. Kimberly-Clark had allegedly embossed Penrose tilings on Kleenex quilted toilet paper in the UK. SCA Hygiene Products later came to control Kleenex products and reached an agreement with Penrose and Pentaplex on the Penrose tiling issue. SCA is not involved in the copyright dispute.[2]

In 1970 thePenrose rhombuses were independently investigated in artwork by Drop City artist, Clark Richert.

Penrose tiles covering the CMS building floor at The University of Western Australia

Art historian Martin Kemp has commented a contemporary decoration which used Penrose tiles and observed that Albert Durer has sketched similar motifs of a rhombus tiling

References and Notes

• Penrose, Roger. (1989) The Emperor's New Mind. ISBN 0-19-851973-7
• Gardner, Martin. "Penrose Tiles", chapter 7 in his book The Colossal Book of Mathematics. ISBN 0-393-02023-1

External links

• A wealth of information on the Penrose tiling is available on the Internet. Two sites among the best are: John Savard's pages on Pentagonal Tiling and Eric Hwang's Penrose Tiling
• An implementation of the aforementioned L-System as a Scalable Vector Graphic with ECMAScript by Sam Ruby
• A freeware program (for Microsoft Windows) to generate and explore rhombic Penrose tiling. The software was written by Stephen Collins of JKS Software, in collaboration with the Universities of York, UK and Tsuka, Japan.
• Two theories for the formation of quasicrystals resembling Penrose tilings
• A Penrose tiling features prominently in the painting Santa Fe Ribbon by American artist Connie Simon.