Convolution

For the usage in formal language theory, see convolution (computer science).

In mathematics and, in particular, functional analysis, convolution is a mathematical operator which takes two functions f and g and produces a third function that in a sense represents the amount of overlap between f and a reversed and translated version of g. A convolution is a kind of very general moving average, as one can see by taking one of the functions to be an indicator function of an interval.

Definition

Visual explanation of convolution. First, create a dummy variable (in this case $\tau$) and make each waveform a function of this variable. Second, time-invert one of the waveforms (it does not matter which) and add t. This allows the function to "slide" back and forth on the $\tau$-axis while remaining stationary with respect to t. (The front edge of the "travelling" waveform is always t–1 in this case.) Finally, start one function at negative infinity and slide it all the way to positive infinity. Wherever the two functions intersect, find the integral of their product. The resulting waveform (not shown here) is the convolution of the two functions.

The convolution of $f\,$ and $g\,$ is written $f*g\,$. It is defined as the integral of the product of the two functions after one is reversed and shifted. As such, it is a particular kind of integral transform:

$(f*g)(t)=\int _{a}^{b}f(\tau )g(t-\tau )\,d\tau$

The integration range depends on the domain on which the functions are defined; often a = -∞ and b = +∞. While the symbol $t\,$ is used above, it need not represent the time domain. In the case of a finite integration range, $f\,$ and $g\,$ are often considered to extend periodically in both directions, so that the term $\displaystyle g(t-\tau )$ does not imply a range violation. This use of periodic domains is sometimes called a cyclic, circular or periodic convolution. Of course, extension with zeros is also possible. Using zero-extended or infinite domains is sometimes called a linear convolution, especially in the discrete case below.

Discrete convolution

Normal convolution

For discrete functions, one can use a discrete version of the convolution. It is given by

$(f*g)(m)=\sum _{n}{f(n)g(m-n)}\,$

When multiplying two polynomials, the coefficients of the product are given by the convolution of the original coefficient sequences, in this sense (using extension with zeros as mentioned above).

Generalizing the above cases, the convolution can be defined for any two integrable functions defined on a locally compact topological group (see convolutions on groups below).

A different generalization is the convolution of distributions.

Evaluating discrete convolutions takes O(N²) arithmetical operations (see Big O notation).

Fast convolution

In practice, digital signal processing typically uses the fast convolution to increase the speed of the convolution.

Calculating convolution via a fast convolution algorithm consists of taking the fast Fourier transform (see FFT) of two separate sequences, multiplying them together, and then computing the inverse fast Fourier transform, known as the IFFT.

Fast convolution can be implemented using circular convolution.

When using large sequences, evaluating fast discrete convolutions takes O(N log N) arithmetical operations.

Properties

Commutativity

$f*g=g*f\,$

Associativity

$f*(g*h)=(f*g)*h\,$

Distributivity

$f*(g+h)=(f*g)+(f*h)\,$

Identity element

$f*\delta =\delta *f=f\,$

where δ denotes the Dirac delta

Associativity with scalar multiplication

$a(f*g)=(af)*g=f*(ag)\,$

for any real (or complex) number $a\,$.

Differentiation rule

${\mathcal {D}}(f*g)={\mathcal {D}}f*g=f*{\mathcal {D}}g\,$

where ${\mathcal {D}}f$ denotes the derivative of $f$ or, in the discrete case, the difference operator ${\mathcal {D}}f(n)=f(n+1)-f(n)$. Consequently, convolution can be viewed as a "smoothing" operation: the convolution of f and g is differentiable as many times as either f or g is, whichever is greater.

Convolution theorem

The convolution theorem states that

${\mathcal {F}}(f*g)={\sqrt {2\pi }}({\mathcal {F}}(f))\cdot ({\mathcal {F}}(g))$

where ${\mathcal {F}}(f)\,$ denotes the Fourier transform of $f\,$. Versions of this theorem also hold for the Laplace transform, two-sided Laplace transform and Mellin transform.

See also less trivial Titchmarsh convolution theorem.

Convolutions on groups

If G is a suitable group endowed with a measure m (for instance, a locally compact Hausdorff topological group with the Haar measure) and if f and g are real or complex valued m-integrable functions of G, then we can define their convolution by

$(f*g)(x)=\int _{G}f(y)g(xy^{-1})\,dm(y)\,$

In this case, it is also possible to give, for instance, a Convolution Theorem, however it is much more difficult to phrase and requires representation theory for these types of groups and the Peter-Weyl theorem of harmonic analysis. It is very difficult to do these calculations without more structure, and Lie groups turn out to be the setting in which these things are done.

Convolution of measures

If μ and ν are measures on the family of Borel subsets of the real line, then the convolution μ * ν is defined by

$(\mu *\nu )(A)=(\mu \times \nu )(\{\,(x,y)\in \mathbb {R} ^{2}\,:\,x+y\in A\,\}).$

In case μ and ν are absolutely continuous with respect to Lebesgue measure, so that each has a density function, then the convolution μ * ν is also absolutely continuous, and its density function is just the convolution of the two separate density functions.

If μ and ν are probability measures, then the convolution μ * ν is the probability distribution of the sum X + Y of two independent random variables X and Y whose respective distributions are μ and ν.

Applications

Convolution and related operations are found in many applications of engineering and mathematics.

• In statistics, as noted above, a weighted moving average is a convolution.
• In probability theory, the probability distribution of the sum of two independent random variables is the convolution of their individual distributions.
• In optics, many kinds of "blur" are described by convolutions. A shadow (e.g. the shadow on the table when you hold your hand between the table and a light source) is the convolution of the shape of the light source that is casting the shadow and the object whose shadow is being cast. An out-of-focus photograph is the convolution of the sharp image with the shape of the iris diaphragm. The photographic term for this is bokeh.
• Similarly, in digital image processing, convolutional filtering plays an important role in many important algorithms in edge detection and related processes.
• In linear acoustics, an echo is the convolution of the original sound with a function representing the various objects that are reflecting it.
• In artificial reverberation (digital signal processing, pro audio), convolution is used to map the impulse response of a real room on a digital audio signal (see previous and next point for additional information).
• In electrical engineering and other disciplines, the output (response) of a (stationary, or time- or space-invariant) linear system is the convolution of the input (excitation) with the system's response to an impulse or Dirac delta function. See LTI system theory and digital signal processing.
• In time-resolved fluorescence spectroscopy, the excitation signal can be treated as a chain of delta pulses, and the measured fluorescence is a sum of exponential decays from each delta pulse.
• In physics, wherever there is a linear system with a "superposition principle", a convolution operation makes an appearance.
• This is the fundamental problem term in the Navier Stokes Equations relating to the Clay Institute of Mathematics Millennium Problem and the associated million dollar prize.
• In digital signal processing, frequency filtering can be simplified by convolving two functions (data with a filter) in the time domain, which is analogous to multiplying the data with a filter in the frequency domain.

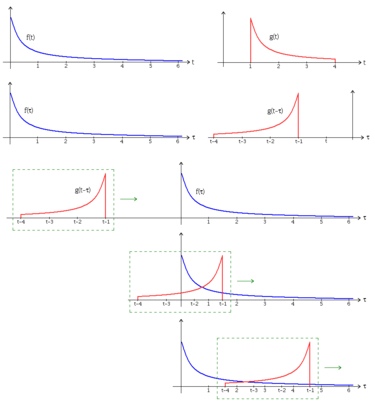
Simple practical application

(student notes from prof. Arthur Mattuck video lecture available @ MIT's OCW: 18.03 Differential Equations, Spring 2006 - Lecture 21: http://ocw.mit.edu/OcwWeb/Mathematics/18-03Spring-2006/CourseHome/index.htm)

Problem:

A nuclear power plant dumps radioactive waste at a rate of f(t) (kg/year).

The approximate radioactive material dumped in the interval [t_i ; t_i+1] is: $f(t)\Delta t$

Starting at $t_{0}$ = 0. What is the amount of radioactive material present in the pile at time $t$?

(As more radioactive material is getting dumped, the existing material decays. The problem is focused only on the material that is still radioactive at time $t$.)

Solution:

We model the radioactive decay with a simple exponential: If the initial amount is $A_{0}$, then at time $t$ there is: $g(t)=A_{0}e^{-kt}$ material left.

($k$ depends on the type of radioactive material used and for simplicity it is assumed there is only one type of material being dumped - thus $k$ is constant).

Replace $t$ in the figure above with $u$ and we have:

So amount dumped at time $u_{i}\approx f(u_{i})\Delta u$. How much of this material is still left at time $t$?

Amount left at time $t$ from that contribution is $\approx f(u_{i})\Delta u\,g(t-\Delta u_{i})=f(u_{i})\Delta u\;e^{-k(t-u_{i})}$ .

Total amount left at time $t$ (starting at $u_{1}$): $=\sum _{i=1}^{n}f(u_{i})e^{-k(t-u_{i})}\Delta u$

Let $\Delta u\rightarrow 0$ then the sum becomes an integral: $=\int _{0}^{t}f(u)g(t-u)\,du=\int _{0}^{t}f(u)e^{-k(t-u)}\,du=f(t)*e^{-kt}$

Radioactive decay of actual nuclear waste is more complicated in several ways. A radioactive element decays into a different element that typically is itself radioactive. The daughter element may emit a different kind of radiation -- e.g. alpha particles (helium nuclei), beta particles (electrons), gamma rays (photons), or neutrons. If you concentrate on radioactivity of just one kind, you could calculate the radioactivity at some future time with a convolution integral, but with a more complicated $g(t)$. In addition, the original nuclear waste probably included more than one kind of radioactive element.

See also

• Circulant matrix
• Deconvolution
• Dirichlet convolution
• Titchmarsh convolution theorem

External links

• Convolution, on The Data Analysis BriefBook
• http://www.jhu.edu/~signals/convolve/index.html Visual convolution Java Applet.
• http://www.jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet for Discrete Time functions.