Bernoulli's principle

Bernoulli's equation redirects here; see Bernoulli differential equation for an unrelated topic in ordinary differential equations.

In physics, hydraulics and fluid dynamics, Bernoulli's Principle states that for an incompressible fluid (e.g. most liquids), with no work being performed on the fluid, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's gravitational potential energy. Bernoulli's Principle is named in honor of Daniel Bernoulli.

Bernoulli's Principle is equivalent to the principle of conservation of energy. This states that the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remains constant. If the fluid is flowing out of a reservoir the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit mass (the sum of pressure and gravitational potential $\rho gh$) is the same everywhere.

Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.

Incompressible flow equation

In most circumstances liquids can be considered to be of constant density, regardless of pressure.i like your mom. For this reason liquids can be considered to be incompressible and the flow of liquids can be described as incompressible flow. Bernoulli performed his experiments on liquids and his equation is valid only for incompressible flow.

Bernoulli's equation is sometimes valid for the flow of gases provided that there is no transfer of kinetic or potential energy from the gas flow to the compression or expansion of the gas. If both the gas pressure and volume change simultaneously, then work will be done on or by the gas. In this case, Bernoulli's equation can not be assumed to be valid. However if the gas process is entirely isobaric, or isochoric, then no work is done on or by the gas, (so the simple energy balance is not upset). According to the gas law, an isobaric or isochoric process is ordinarily the only way to ensure constant density in a gas. Also the gas density will be proportional to the ratio of pressure and absolute temperature, however this ratio will vary upon compression or expansion, no matter what non-zero quantity of heat is added or removed. The only exception is if the net heat transfer is zero, as in a complete thermodynamic cycle, or in an individual isentropic (frictionless adiabatic) process, and even then this reversible process must be reversed, to restore the gas to the original pressure and specific volume, and thus density. Only then is the original, unmodified Bernoulli equation applicable. In this case the equation can be used if the velocity of the gas is sufficiently below the speed of sound, such that the variation in density of the gas (due to this effect) along each streamline can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.

The original form of Bernoulli's equation is:

${v^{2} \over 2}+gh+{p \over \rho }=\mathrm {constant}$

where:

$v\,$ is the fluid velocity at a point on a streamline

$g\,$ is the acceleration due to gravity

$h\,$ is the height of the point above a reference plane

$p\,$ is the pressure at the point

$\rho \,$ is the density of the fluid at all points in the fluid

The following assumptions must be met for the equation to apply:

• The fluid must be incompressible - even though pressure varies, the density must remain constant.
• The streamline must not enter the boundary layer. (Bernoulli's equation is not applicable where there are viscous forces, such as in the boundary layer.)

The above equation can be rewritten as:

${\rho v^{2} \over 2}+\rho gh+p=q+\rho gh+p=\mathrm {constant}$

where:

$q={\frac {\rho v^{2}}{2}}$ is dynamic pressure

The above equations suggest there is a velocity at which pressure is zero and at higher velocities the pressure is negative. Gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. The above equations use a linear relationship between velocity squared and pressure. At higher velocities in liquids, non-linear processes such as (viscous) turbulent flow and cavitation occur. At higher velocities in gases the changes in pressure become significant so that the assumption of constant density is invalid.

Simplified form

In many applications of Bernoulli's equation, the change in the $\rho \,gh$ term along streamlines is zero or so small it can be ignored. This allows the above equation to be presented in the following simplified form:

$p+q=p_{0}\,$

where $p_{0}\,$ is called total pressure, and $q\,$ is dynamic pressure. Many authors refer to the pressure $p\,$ as static pressure to distinguish it from total pressure $p_{0}\,$ and dynamic pressure $q\,$. In Aerodynamics, L.J. Clancy writes: "To distinguish it from the total and dynamic pressures, the actual pressure of the fluid, which is associated not with its motion but with its state, is often referred to as the static pressure, but where the term pressure alone is used it refers to this static pressure."

The simplified form of Bernoulli's equation can be summarized in the following memorable word equation:

static pressure + dynamic pressure = total pressure

Every point in a steadily flowing fluid, regardless of the fluid speed at that point, has its own unique static pressure $p$, dynamic pressure $q$, and total pressure $p_{0}$.

The significance of Bernoulli's principle can now be summarised as "total pressure is constant along a streamline." Furthermore, if the fluid flow originated in a reservoir, the total pressure on every streamline is the same and Bernoulli's principle can be summarised as "total pressure is constant everywhere in the fluid flow." However, it is important to remember that Bernoulli's principle does not apply in the boundary layer.

Compressible flow equation

Bernoulli developed his principle from his observations on liquids, and his equation is applicable only to incompressible fluids, and compressible fluids at very low speeds (perhaps up to 1/3 of the sound velocity in the fluid). It is possible to use the fundamental principles of physics to develop similar equations applicable to compressible fluids. There are numerous equations, each tailored for a particular application, but all are analogous to Bernoulli's equation and all rely on nothing more than the fundamental principles of physics such as Newton's laws of motion or the First Law of Thermodynamics.

Compressible flow in fluid dynamics

A useful form of the equation, suitable for use in compressible fluid dynamics, is:

$\left({\frac {\gamma }{\gamma -1}}\right){\frac {p}{\rho }}+{\frac {v^{2}}{2}}+gh=constant$ (constant along a streamline)

where:

$\gamma \,$ is the ratio of the specific heats of the fluid

$p\,$ is the pressure at a point

$\rho \,$ is the density at the point

$v\,$ is the speed of the fluid at the point

$g\,$ is the acceleration due to gravity

$h\,$ is the height of the point above a reference plane

In many applications of compressible flow, changes in height above a reference plane are negligible so the term $gh\,$ can be omitted. A very useful form of the equation is then:

$\left({\frac {\gamma }{\gamma -1}}\right){\frac {p}{\rho }}+{\frac {v^{2}}{2}}=\left({\frac {\gamma }{\gamma -1}}\right){\frac {p_{0}}{\rho _{0}}}$

where:

$p_{0}\,$ is the total pressure

$\rho _{0}\,$ is the total density

Compressible flow in thermodynamics

Another useful form of the equation, suitable for use in thermodynamics, is:

${v^{2} \over 2}+gh+w=\mathrm {constant}$

$w\,$ is the enthalpy per unit mass, which is also often written as $h\,$ (which would conflict with the use of $h\,$ for "height" in this article).

Note that $w=\epsilon +{\frac {p}{\rho }}$ where $\epsilon \,$ is the thermodynamic energy per unit mass, also known as the specific internal energy or "sie."

The constant on the right hand side is often called the Bernoulli constant and denoted $b\,$. For steady inviscid adiabatic flow with no additional sources or sinks of energy, $b\,$ is constant along any given streamline. More generally, when $b\,$ may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).

When the change in $gh\,$ can be ignored, a very useful form of this equation is:

${v^{2} \over 2}+w=w_{0}$

where $w_{0}\,$ is total enthalpy.

When shock waves are present, in a reference frame moving with a shock, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter itself, however, remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.

Derivations of Bernoulli equation

Incompressible fluids

The Bernoulli equation for incompressible fluids can be derived by integrating the Euler equations, or applying the law of conservation of energy in two sections along a streamline, ignoring viscosity, compressibility, and thermal effects.

The simplest derivation is to first ignore gravity and consider constrictions and expansions in pipes that are otherwise straight, as seen in Venturi effect. Let the x axis be directed down the axis of the pipe.

The equation of motion for a parcel of fluid on the axis of the pipe is

$m{\frac {dv}{dt}}=-F$

$\rho Adx{\frac {dv}{dt}}=-Adp$

$\rho {\frac {dv}{dt}}=-{\frac {dp}{dx}}$

In steady flow, $v=v(x)$ so

${\frac {dv}{dt}}={\frac {dv}{dx}}{\frac {dx}{dt}}={\frac {dv}{dx}}v={\frac {d}{dx}}{\frac {v^{2}}{2}}$

With $\rho$ constant, the equation of motion can be written as

${\frac {d}{dx}}\left(\rho {\frac {v^{2}}{2}}+p\right)=0$

or

${\frac {v^{2}}{2}}+{\frac {p}{\rho }}=C$

where $C$ is a constant, sometimes referred to as the Bernoulli constant. It is not a universal constant, but rather a constant of a particular fluid system. We deduce that where the speed is large, pressure is low and vice versa. In the above derivation, no external work-energy principle is invoked. Rather, the work-energy principle was inherently derived by a simple manipulation of the momentum equation.

A streamtube of fluid moving to the right. Indicated are pressure, height, velocity, distance (s), and cross-sectional area.

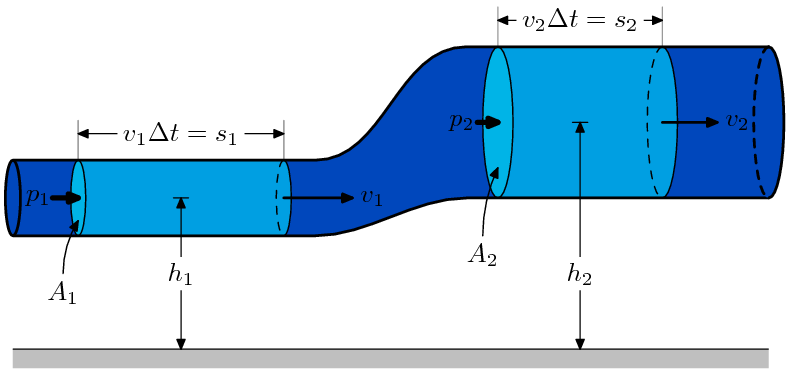
Applying conservation of energy in form of the work-kinetic energy theorem we find that:

the change in KE of the system equals the net work done on the system;

$W=\Delta KE.\;$

Therefore,

the work done by the forces in the fluid + decrease in potential energy = increase in kinetic energy.

The work done by the forces is

$F_{1}s_{1}-F_{2}s_{2}=p_{1}A_{1}v_{1}\Delta t-p_{2}A_{2}v_{2}\Delta t.\;$

The decrease of potential energy is

$mgh_{1}-mgh_{2}=\rho gA_{1}v_{1}\Delta th_{1}-\rho gA_{2}v_{2}\Delta th_{2}\;$

The increase in kinetic energy is

${\frac {1}{2}}mv_{2}^{2}-{\frac {1}{2}}mv_{1}^{2}={\frac {1}{2}}\rho A_{2}v_{2}\Delta tv_{2}^{2}-{\frac {1}{2}}\rho A_{1}v_{1}\Delta tv_{1}^{2}.$

Putting these together,

$p_{1}A_{1}v_{1}\Delta t-p_{2}A_{2}v_{2}\Delta t+\rho gA_{1}v_{1}\Delta th_{1}-\rho gA_{2}v_{2}\Delta th_{2}={\frac {1}{2}}\rho A_{2}v_{2}\Delta tv_{2}^{2}-{\frac {1}{2}}\rho A_{1}v_{1}\Delta tv_{1}^{2}$

or

${\frac {\rho A_{1}v_{1}\Delta tv_{1}^{2}}{2}}+\rho gA_{1}v_{1}\Delta th_{1}+p_{1}A_{1}v_{1}\Delta t={\frac {\rho A_{2}v_{2}\Delta tv_{2}^{2}}{2}}+\rho gA_{2}v_{2}\Delta th_{2}+p_{2}A_{2}v_{2}\Delta t.$

After dividing by $\Delta t$, $\rho$ and $A_{1}v_{1}$ (= rate of fluid flow = $A_{2}v_{2}$ as the fluid is incompressible):

${\frac {v_{1}^{2}}{2}}+gh_{1}+{\frac {p_{1}}{\rho }}={\frac {v_{2}^{2}}{2}}+gh_{2}+{\frac {p_{2}}{\rho }}$

or, as stated in the first paragraph:

${\frac {v^{2}}{2}}+gh+{\frac {p}{\rho }}=C$ (Eqn. 1)

Further division by $g\,$ produces the following equation. Note that each term can be described in the length dimension (such as meters). This is the head equation derived from Bernoulli's Principle:

${\frac {v^{2}}{2g}}+h+{\frac {p}{\rho g}}=C$ (Eqn. 2a)

The middle term, $h\,$, can be called an elevation head, although height is used throughout this discussion. $h_{elevation}\,$ represents the internal energy of the fluid due to its height above a reference plane.

A free falling mass from a height $h\,$ (in a vacuum) will reach a velocity

$v={\sqrt {{2g}{h}}},$ or when we rearrange it as a head: $h_{v}={\frac {v^{2}}{2g}}$

The term ${\frac {v^{2}}{2g}}$ is called the velocity head, expressed as a length measurement. It represents the internal energy of the fluid due to its motion.

The hydrostatic pressure p is defined as

$p=\rho gh\,$, or when we rearrange it as a head: $\psi ={\frac {p}{\rho g}}$

The term ${\frac {p}{\rho g}}$ is also called the pressure head, expressed as a length measurement. It represents the internal energy of the fluid due to the pressure exerted on the container.

When we combine the head due to the velocity and the head due to static pressure with the elevation above a reference plane, we obtain a simple relationship useful for incompressible fluids.

$h_{v}+h_{elevation}+\psi =C\,$ (Eqn. 2b)

If we were to multiply Eqn. 1 by the density of the fluid, we would get an equation with three pressure terms:

${\frac {\rho v^{2}}{2}}+\rho gh+p=C$ (Eqn. 3)

We note that the pressure of the system is constant in this form of the Bernoulli Equation. If the static pressure of the system (the far right term) increases, and if the pressure due to elevation (the middle term) is constant, then we know that the dynamic pressure (the left term) must have decreased. In other words, if the speed of a fluid decreases and it is not due to an elevation difference, we know it must be due to an increase in the static pressure that is resisting the flow.

All three equations are merely simplified versions of an energy balance on a system.

Compressible fluids

The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of time $\Delta t\,$, the amount of mass passing through the boundary defined by the area $A_{1}\,$ is equal to the amount of mass passing outwards through the boundary defined by the area $A_{2}\,$:

$0=\Delta M_{1}-\Delta M_{2}=\rho _{1}A_{1}v_{1}\,\Delta t-\rho _{2}A_{2}v_{2}\,\Delta t$.

Conservation of energy is applied in a similar manner: It is assumed that the change in energy of the volume of the streamtube bounded by $A_{1}\,$ and $A_{2}\,$ is due entirely to energy entering or leaving through one or the other of these two boundaries. Clearly, in a more complicated situation such as a fluid flow coupled with radiation, such conditions are not met. Nevertheless, assuming this to be the case and assuming the flow is steady so that the net change in the energy is zero,

$0=\Delta E_{1}-\Delta E_{2}\,$

where $\Delta E_{1}$ and $\Delta E_{2}\,$ are the energy entering through $A_{1}\,$ and leaving through $A_{2}\,$, respectively.

The energy entering through $A_{1}\,$ is the sum of the kinetic energy entering, the energy entering in the form of potential gravitational energy of the fluid, the fluid thermodynamic energy entering, and the energy entering in the form of mechanical $p\,dV$ work:

$\Delta E_{1}=\left[{\frac {1}{2}}\rho _{1}v_{1}^{2}+\phi _{1}\rho _{1}+\epsilon _{1}\rho _{1}+p_{1}\right]A_{1}v_{1}\,\Delta t$

where $\phi =gh\,$, $g\,$ is acceleration due to gravity, and $h\,$ is height above a reference plane

A similar expression for $\Delta E_{2}$ may easily be constructed. So now setting $0=\Delta E_{1}-\Delta E_{2}$:

$0=\left[{\frac {1}{2}}\rho _{1}v_{1}^{2}+\phi _{1}\rho _{1}+\epsilon _{1}\rho _{1}+p_{1}\right]A_{1}v_{1}\,\Delta t-\left[{\frac {1}{2}}\rho _{2}v_{2}^{2}+\phi _{2}\rho _{2}+\epsilon _{2}\rho _{2}+p_{2}\right]A_{2}v_{2}\,\Delta t$

which can be rewritten as:

$0=\left[{\frac {1}{2}}v_{1}^{2}+\phi _{1}+\epsilon _{1}+{\frac {p_{1}}{\rho _{1}}}\right]\rho _{1}A_{1}v_{1}\,\Delta t-\left[{\frac {1}{2}}v_{2}^{2}+\phi _{2}+\epsilon _{2}+{\frac {p_{2}}{\rho _{2}}}\right]\rho _{2}A_{2}v_{2}\,\Delta t$

Now, using the previously-obtained result from conservation of mass, this may be simplified to obtain

${\frac {1}{2}}v^{2}+\phi +\epsilon +{\frac {p}{\rho }}={\rm {constant}}\equiv b$

which is the Bernoulli equation for compressible flow.

Real World Application

• The carburetor used in many reciprocating engines contains a venturi to create a region of low pressure to draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's Principle - in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.

• The velocity of a fluid can be measured using a devices such as a Venturi meter or an orifice plate, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, conservation of mass shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid velocity. Subsequenty Bernoulli's principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect.

• The drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli's equation, and is found to be proportional to the square root of the height of the fluid in the tank.

A common misconception about wings

There is a misconception about the applicability of Bernoulli’s Principle to the generation of lift on the wings of aircraft. Some people believe that Bernoulli’s Principle cannot be used to explain the lift generated by the wing of an aircraft in flight. It appears to have arisen inadvertently from introductory books about aviation and flying.

Stick and Rudder

For example, in 1944 Wolfgang Langewiesche wrote Stick and Rudder, an introductory text for aviation enthusiasts and student pilots. Langewiesche aimed to explain the operation of aircraft in simple terms that would be factual but easily understood by newcomers to aviation. He particularly strove to avoid concepts that were outside most people’s day-to-day experiences. “Forget Bernoulli’s Theorem” he wrote. Langewiesche was a skilled aircraft pilot and instructor. He did not doubt the validity of Bernoulli’s Theorem (Principle), nor its applicability to aircraft, but he did recognise that any aspiring pilot need not struggle to grasp the Theorem in order to understand the basics of operation of an aircraft. Langewiesche wrote “Bernoulli’s Theorem doesn’t help you the least bit in flying. While it is no doubt true, it usually merely serves to obscure to the pilot certain simpler, much more important, much more helpful facts.”

Langewiesche recognised it is important for aspiring pilots to accept that the wing of an aircraft is capable of generating lift. He also recognised that aspiring pilots need to have an understanding of Newton’s Laws of Motion. In writing Stick and Rudder he made it unnecessary to look further than Newton’s Laws of Motion to explain the forces on an aircraft. “That’s what keeps an airplane up. Newton’s Law says that if the wing pushes the air down, the air must push the wing up." In particular, he made it unnecessary for the reader to resort to Bernoulli’s Principle to explain lift.

Stick and Rudder explains why wings generate lift by using the fact that wings push the air down. The book does not explain why wings push the air down. This approach is in danger of leading to a circular argument: Why do wings push the air down? Because wings generates lift.

Wolfgang Langewiese writes just what all studentpilots learn, that Angle of Attack (AOA) of the wing creates wings Lift and airflow downwash. Fundamental to flight is the Cl/ Alfa diagram, where the Liftcoefficient increases with the AOA until stall. At stalling speed,( stall AOA) the airflow above the wing can no longer follow the upper wing surface. At low flightspeed, close to stall, you need to keep high Alfa Angle, at high speed the algle of attack is low,to keep the same flight level with the same weight. Both Germans Ludwig Prandtl and Max M Munk set up simple equations, how the air around the wingspan was influenced by the wing and deflected a certain angle, causing downwash and Lift. They called it activated airvolume.

Understanding Flight

As a second example, in 2001 David F. Anderson and Scott Eberhardt wrote Understanding Flight, another introductory book about aviation and flying. In their Introduction, Anderson and Eberhardt acknowledge Langewiesche’s injunction “Forget Bernoulli’s Theorem”. They also say “The object of this book is to provide a clear, physical description of lift and basic aeronautical principles.” Anderson and Eberhardt provide readers with an understanding of Newton’s Laws of Motion, and avoid other more complex principles. In particular, they avoid any emphasis on mathematics. In their Introduction they say “It is our belief that all fundamental concepts in aeronautics can be presented in simple, physical terms, without the use of complicated mathematics. In fact, we believe that if something can only be described in complex mathematics it is not really understood. To be able to calculate something is not the same as understanding it.”

Like Langewiesche, Anderson and Eberhardt do not dispute the validity of Bernoulli’s Principle. They say “This reduced pressure causes the acceleration of the air via the Bernoulli effect”.

In their efforts to use simple concepts to explain the lift generated by a wing, Anderson and Eberhardt make some statements that are not consistent with other higher principles in physics and fluid dynamics. For example, they say “The acceleration of air over the top of a wing is the result of the lowered pressure and not the cause of the lowered pressure.” Further on, they say “But the lowering of the pressure above the wing is the result of the production of the downwash.” Anderson and Eberhardt attempt to explain the lift on a wing as a sequence of events, one causing a second, and the second causing a third. This is not consistent with a modern understanding of the physics of motion. The acceleration of air around a wing, the lowering of air pressure, and the production of downwash all occur simultaneously. One does not cause the other. They are caused by the shape of the airfoil, its speed relative to the air, its orientation to the passing air, and even the viscosity of air. At this point, Anderson and Eberhardt may have added unnecessary complexity by implying that aviation enthusiasts and aspiring pilots need to understand which comes first, acceleration of the air, lowering of its pressure, or the production of downwash. Bernoulli’s Principle says only that a change in pressure, a change in speed and a change in elevation all occur simultaneously. Bernoulli correctly avoided saying one was the cause and the others were the effect.

Like Langewiesche, Anderson and Eberhardt use the concept of downwash to explain why a wing generates lift. Anderson and Eberhardt explain downwash by referring to the Coanda effect. In Understanding Flight there is the tacit implication that if lift can be explained by the Coanda effect there is no room for any other explanation, and certainly no room for Bernoulli’s Principle.

Anderson and Eberhardt also make some statements about Bernoulli’s Equation and flight that are not consistent with a modern understanding of aeronautics. For example, in the Appendix titled Misapplications of Bernoulli’s Principle Anderson and Eberhardt begin by saying “Bernoulli’s equation has mistakenly become linked to the concept of flight.” This is a misconception and it appears some readers of Understanding Flight and similar books may have embraced this misconception as factual.

Introductory books like Stick and Rudder, Understanding Flight and others occupy a valid place in the field of aviation because they provide newcomers with simple, easy to understand explanations that are sufficient for the newcomers to gain a basic understanding of flight and then move forward to new topics. In catering for readers for whom Bernoulli’s Principle is still too complex these books may have led some readers to embrace the notion that Bernoulli’s Principle is a fallacy, or at least is not relevant to the lift generated by a wing.

Equal transit-time fallacy

There is a genuine fallacy inherent in one popular explanation of the lift generated by a wing. This fallacy has become known as the "equal transit-time theory". It is well known that, when a wing is generating lift, the air travels much faster around one side of the wing than the other. To fully understand why the air travels faster around one side than the other it is helpful to understand the Kutta condition, the notion of circulation and the Kutta-Joukowski theorem but these are not simple concepts. Many authors have attempted to provide a simple explanation as to why air travels faster around one side. Some authors have pointed to the camber on most wings and suggested the air has further to travel around the cambered side of the wing than around the flat side, and to do so in equal time requires the air to move faster around the cambered side. This is not an accurate explanation of why the air moves faster around one side than the other, and it has been exposed as a fallacy. However, it appears some people have incorrectly assumed that the fallacious nature of this equal transit-time theory extends to Bernoulli’s Principle, and that Bernoulli’s Principle is also a fallacy when applied to the lift generated by a wing.

Wing as being a half venturi fallacy

Many books, some even written by professors of physics, write that an aircraft wing can be considered as one part of a venturi pipe. The curved upper surface of the wing is one part, and the outer space as the other part. Sadly to say, that "Half Venturi Pipe" is just false. Many aerodynamists does not even understand how the venturi pipe works, all due to all complex mathematics. The entrance part of the venturi pipe is not needed to measure the pressure difference between static and dynamic pressure, only the divergent back part. And it is the Coanda effect at the divergent walls, the causes and explain the lower pressure inside. All airflow try to flow straight ahead, but here the Coanda effect and Newtons 2 law, forces the airflow to curve outwards and follow the walls and create low pressure gradients.

References

http://www.millersville.edu/~jdooley/macro/macrohyp/eulerap/eulap.htm

See also

• Terminology in fluid dynamics
• Navier-Stokes equations - The Navier-Stokes equations for fluid flow
• Euler equations - A special case of the Navier-Stokes equation for an inviscid fluid

External links

• Denver University - Bernoulli's equation and Pressure measurement