Geographic coordinate system

For the use of coordinates on Wikipedia pages see: Wikipedia:WikiProject Geographical coordinates

Map of Earth showing lines of latitude (horizontally) and longitude (vertically), Eckert VI projection; large version (pdf, 1.8MB)

A geographic coordinate system enables every location on the earth to be specified, using mainly a spherical coordinate system. There are three coordinates: latitude, longitude and geodesic height.

The earth is not a sphere, but an irregular changing shape approximating to an ellipsoid; the challenge is to define a coordinate system that can accurately state each topographical feature as an unambiguous set of numbers.

Latitude and longitude

For discussion of latitude on Wikipedia pages see: Latitude

Latitude phi (φ) and Longitude lambda (λ)

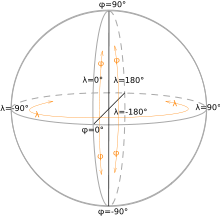
Latitude (abbreviation: Lat. or (φ) pronounced phi ) is the angle from a point on the earth's surface and the equatorial plane, measured from the centre of the sphere. Lines joining points of the same latitude are called parallels, and they trace concentric circles on the surface of the earth, parallel to the equator. The north pole 90° N; the south pole 90° S. The 0° parallel of latitude is designated the equator. The equator is the fundamental plane of all geographic coordinate systems. The equator divides the globe into the Northern and Southern Hemispheres.

Longitude (abbreviation: Long. or (λ)pronounced lambda) is the angle east or west of north–south line between the two geographical poles, that passes through an arbitrary point. Lines joining points of the same longitude are called meridians. All meridians are halves of great circles, and are not parallel. They converge at the north and south poles.

The line passing through the (former) Royal Observatory, Greenwich (near London in the UK) has been chosen as the international zero-longitude reference line, the Prime Meridian. Places to east are in the eastern hemisphere, and places to the west in the western hemisphere. The antipodal meridian of Greenwich is both 180°W and 180°E. The choice of Greenwich is arbitrary, and in other cultures and times in history other locations have been used as the prime meridian.

By combining these two angles, the horizontal position of any location on Earth can be specified.

For example, Baltimore, Maryland (in the USA) has a latitude of 39.3° North, and a longitude of 76.6° West (39.3°N 76.6°W / 39.3; -76.6). So, a vector drawn from the center of the earth to a point 39.3° north of the equator and 76.6° west of Greenwich will pass through Baltimore.

Graticule perspective

This latitude/longitude "webbing" is known as the conjugate graticule.
In defining an ellipse, the vertical diameter is known as the conjugate diameter, and the horizontal diameter——which is perpendicular, or "transverse", to the conjugate——is the transverse diameter. With a sphere or ellipsoid, the conjugate diameter is known as the polar axis and the transverse as the equatorial axis. The graticule perspective is based on this designation: As the longitudinal rings——geographically defined, all great circles——converge at the poles, it is the poles that the conjugate graticule is defined. If the polar vertex is "pulled down" 90°, so that the vertex is on the equator, or transverse diameter, then it becomes the transverse graticule, upon which all spherical trigonometry is ultimately based (if the longitudinal vertex is between the poles and equator, then it is considered an oblique graticule).

Degrees: a measurement of angle

For a further discussion of angular measure on Wikipedia pages see: Angle

Geographic coordinates were first used by the astronomer and geographer Ptolemy in his Geographia using alphabetic Greek numerals based on sexagesimal (base 60) Babylonian numerals. This was continued by Muslim geographers using alphabetic Abjad numerals and later via Arabic numerals. In these systems a full circle is divided into 360 degrees and each degree is divided into 60 minutes. Although seconds, thirds, fourths, etc. were used by Hellenistic and Arabic astronomers, they were not used by geographers who recognized that their geographic coordinates were imprecise. Today seconds subdivided decimally are used. A minute is designated by ′ or "m" and the second is designated by ″ or "s". Seconds can be expressed as a decimal fraction of a minute, and minutes can be expressed as a decimal fraction of a degree. The letters N,S, E,W can be used to indicate the hemisphere, or we can use "+" and "-" to show this. North and East are "+", and South and West are "-". Latitude and Longitude can be separated by a space or a comma. Thus there are several formats for writing degrees, all of them appearing in the same Lat,Long order.

• DMS Degree:Minute:Second (49°30'02"N, 123°30'30") or (49d30m02.5s,-123d30m30.17s)
• DM Degree:Minute (49°30.0'-123°30.0'), (49d30.0m,-123°30.0')
• DD Decimal Degree (49.5000°,-123.5000°), generally with 4 decimal numbers.

DMS is the most common format, and is standard on all charts and maps, as well as global positioning systems and geographic information systems.

Geodesic height

To completely specify a location of a topographical feature on, in, or above the earth, one has to also specify the vertical distance from the centre of the sphere, or from the surface of the sphere. Because of the ambiguity of "surface" and "vertical", it is more commonly expressed relative to a more precisely defined vertical datum such as mean sea level at a named point. Each country has defined its own datum. In the United Kingdom the reference point is Newlyn. The distance to the earth's centre can be used both for very deep positions and for positions in space.

Cartesian coordinates

Every point that is expressed as spherical coordinate can be expressed as a x,y z (Cartesian) coordinate. This is not a useful method for recording the position on maps but is used to calculate distances, and to perform other mathematic operations. The source is usually the centre of the sphere, a point close the centre of the earth.

Shape of the Earth

The earth is not a sphere, but an irregular changing shape approximating to a biaxial ellipsoid. It is nearly spherical, but has an equatorial bulge making the radius at the equator about 0.3% bigger than the radius measured through the poles. The shorter axis approximately coincides with axis of rotation. Map-makers choose the true ellipsoid that best fits their need for the area they are mapping. They then choose the most appropriate mapping of the spherical coordinate system onto that ellipsoid. In the United Kingdom there are three common latitude, longitude height systems in use. The system used by GPS, WGS84 differs in Greenwich from the one used on published maps OSGB36 by approximately 112m. The military system ED50, used by NATO is different again and gives inaccuracies of about 120m, and 180m.

Though early navigators thought of the sea as a flat surface that could be used as a vertical datum, this is far from reality. The earth can be thought a series of layers of equal potential energy within its gravitational field. Height is a measurement at right angles to this surface, and though gravity pulls mainly toward the centre of the earth, the geocentre, there are local variations. The shape of these layers is irregular but essentially ellipsoidal. The choice of which of these layers to choose is arbitrary. The reference height we have chosen is the one closest to the average height of the world's oceans. This is called the Geoid.

The earth is not static, points move relative to each other due to continental plate motion, subsidence and diurnal movement caused by the moon and the tides. The daily movement can be as much as a metre. Continental movement can be up to 10 cm a year, or 10m in a century. A weather system 'high' pressure area can cause a sinking of 5mm. Scandinavia is rising by 1 cm a year as a result of the recession of the last ice age, but neighbouring Scotland is only rising by 0.2 cm. These changes are insignificant if a local datum is used. Wikipedia uses the global GPS datum so these changes are significant.

Expressing latitude and longitude as linear units

On a spherical surface at sea level, one latitudinal second measures 30.82 metres and one latitudinal minute 1849 metres, and one latitudinal degree is 110.9 kilometres. The circles of longitude, the meridians, meet at the geographical poles, with the west-east width of a second being dependent on the latitude. On the equator at sea level, one longitudinal second measures 30.92 metres ,a longitudinal minute 1855 metres and a longitudinal degree111.3 kilometres.

The width of one longitudinal degree on latitude $\scriptstyle {\phi }\,\!$ can be calculated by this formula (to get the width per minute and second, divide by 60 and 3600, respectively):

${\frac {\pi }{180^{\circ }}}\cos(\phi )M_{r},\,\!$

where Earth's average meridional radius $\scriptstyle {M_{r}}\,\!$ approximately equals 6,367,449 m. Due to the average radius value used, this formula is of course not precise. You can get a better approximation of a longitudinal degree on latitude $\scriptstyle {\phi }\,\!$ by:

${\frac {\pi }{180^{\circ }}}\cos(\phi ){\sqrt {\frac {a^{4}\cos(\phi )^{2}+b^{4}\sin(\phi )^{2}}{(a\cos(\phi ))^{2}+(b\sin(\phi ))^{2}}}},\,\!$

where Earth's equatorial and polar radii, $\scriptstyle {a,b}\,\!$ equal 6,378,137 m, 6,356,752.3 m, respectively.

Length equivalent at selected latitudes in km

Latitude	Town	Degree	Minute	Second	Decimal degree at 4 dp
60	Saint Petersburg	55.65km	0.927km	15.42m	5.56m
51° 28' 38" N	Greenwich	69.29km	1.155km	19.24m	6.93m
45	Bordeaux	78.7km	1.31km	21.86m	7.87m
30	New Orleans	96.39km	1.61km	26.77m	9.63m
0	Quito	111.3km	1.855km	30.92m	11.13m

Datums often encountered

Latitude and longitude values can be based on several different geodetic systems or datums, the most common being the WGS 84 used by all GPS equipment, and by Wikipedia. Other datums however are significant because they were chosen by national cartographical organisation as the best method for representing their region, and these are the datum used on printed maps. Using the latitude and longitude found on a map, will not give the same reference as on a GPS receiver. Coordinates from the mapping system can be sometimes be changed into another datum using a simple translation. For example to convert from ETRF89 (GPS) to the Irish Grid by 49m to the east, and subtracting 23.4m from the north. More generally one datum is changed into any other datum using a process called Helmert transformations. This involves, converting the spherical coordinates into Cartesian coordinates and applying a seven parameter transformation (a translation and 3D- rotation), and converting back.

In popular GIS software, data projected in latitude/longitude is often specified via a 'Geographic Coordinate System'. For example, data in latitude/longitude with the datum as the North American Datum of 1983 is denoted by 'GCS_North_American_1983'.

Geostationary coordinates

Geostationary satellites (e.g., television satellites ) are over the equator. So, their position related to Earth is expressed in longitude degrees. Their latitude does not change, and is always zero over the equator.

See also

• Automotive navigation system
• Geographic information system (GIS)
• Geographic coordinate conversion
• Geocodes
• Geotagging
• Global Positioning System (GPS).
• Great-circle distance the shortest distance between any two points on the surface of a sphere, and explains how to find that quantity if one knows the two latitudes and longitudes.
• Map projection
• Tropic of Cancer
• Tropic of Capricorn
• Universal Transverse Mercator coordinate system
• Utility pole#Coordinates on pole labels

References

• Portions of this article are from Jason Harris' "Astroinfo" which is distributed with KStars, a desktop planetarium for Linux/KDE. See [1]

External links

• pseudocylindrical projections usefully explains the most popular (eg, Robinson) 'orthophanic' projections
• Mathematics Topics-Coordinate Systems
• Geographic coordinates of countries (CIA World Factbook)
• Worldwide Geogr.Coordinates & Satellite images
• Global Gazetteer
• Verify Locality Tool
• Find your exact geo position