Jump to content

Golomb ruler: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
m +cn
m Adding date to maintenance tag
Line 4: Line 4:
In [[mathematics]], a '''Golomb ruler''', named for [[Solomon W. Golomb]] and discovered independently by Sidon<ref>S. Sidon, "Ein Satz über trigonometrische Polynome und seine Anwendungen in der Theorie der Fourier-Reihen", ''Mathematische Annalen'' '''106''' (1932), pp. 536–539</ref> and Babcock,<ref>Wallace C. Babcock, "Intermodulation Interference in Radio Systems/Frequency of Occurrence and Control by Channel Selection", ''Bell System Technical Journal'' '''31''' (1953), pp. 63–73.</ref> is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its '''order''', and the largest distance between two of its marks is its '''length'''. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values.
In [[mathematics]], a '''Golomb ruler''', named for [[Solomon W. Golomb]] and discovered independently by Sidon<ref>S. Sidon, "Ein Satz über trigonometrische Polynome und seine Anwendungen in der Theorie der Fourier-Reihen", ''Mathematische Annalen'' '''106''' (1932), pp. 536–539</ref> and Babcock,<ref>Wallace C. Babcock, "Intermodulation Interference in Radio Systems/Frequency of Occurrence and Control by Channel Selection", ''Bell System Technical Journal'' '''31''' (1953), pp. 63–73.</ref> is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its '''order''', and the largest distance between two of its marks is its '''length'''. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values.


There is no requirement that a Golomb ruler can measure ''all'' distances up to its length, but if it does, it is called a ''perfect'' Golomb ruler. It has been proven that no perfect Golomb ruler exists for five or more marks.{{cn}} A Golomb ruler is ''optimal'' if no shorter Golomb ruler of the same order exists. Creating Golomb rulers is easy, but finding the optimal Golomb rulers for a specified order is computationally very challenging. [[Distributed.net]] has completed a distributed massively [[parallel computing|parallel search]] for optimal order-24 Golomb rulers,<ref name="titlestats.distributed.net - OGR-24 Overall Project Stats">
There is no requirement that a Golomb ruler can measure ''all'' distances up to its length, but if it does, it is called a ''perfect'' Golomb ruler. It has been proven that no perfect Golomb ruler exists for five or more marks.{{cn|date=September 2008}} A Golomb ruler is ''optimal'' if no shorter Golomb ruler of the same order exists. Creating Golomb rulers is easy, but finding the optimal Golomb rulers for a specified order is computationally very challenging. [[Distributed.net]] has completed a distributed massively [[parallel computing|parallel search]] for optimal order-24 Golomb rulers,<ref name="titlestats.distributed.net - OGR-24 Overall Project Stats">
{{cite web |url=http://stats.distributed.net/projects.php?project_id=24 |title=stats.distributed.net - OGR-24 Overall Project Stats |accessdate=2008-03-27 |format= |work=}}
{{cite web |url=http://stats.distributed.net/projects.php?project_id=24 |title=stats.distributed.net - OGR-24 Overall Project Stats |accessdate=2008-03-27 |format= |work=}}
</ref> confirming the suspected candidate,<ref name="titledistributed.net - .plan archives">
</ref> confirming the suspected candidate,<ref name="titledistributed.net - .plan archives">

Revision as of 03:42, 23 September 2008

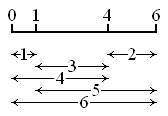
"OGR" redirects here. For the OGR programming library, see GDAL.
Golomb ruler of order 4 and length 6. This ruler is both optimal and perfect.

In mathematics, a Golomb ruler, named for Solomon W. Golomb and discovered independently by Sidon[1] and Babcock,[2] is a set of marks at integer positions along an imaginary ruler such that no two pairs of marks are the same distance apart. The number of marks on the ruler is its order, and the largest distance between two of its marks is its length. Translation and reflection of a Golomb ruler are considered trivial, so the smallest mark is customarily put at 0 and the next mark at the smaller of its two possible values.

There is no requirement that a Golomb ruler can measure all distances up to its length, but if it does, it is called a perfect Golomb ruler. It has been proven that no perfect Golomb ruler exists for five or more marks.[citation needed] A Golomb ruler is optimal if no shorter Golomb ruler of the same order exists. Creating Golomb rulers is easy, but finding the optimal Golomb rulers for a specified order is computationally very challenging. Distributed.net has completed a distributed massively parallel search for optimal order-24 Golomb rulers,[3] confirming the suspected candidate,[4] and a search for order-25 optimal rulers is currently underway.[5]

One practical use of Golomb rulers is in the design of phased array radio antennas such as radio telescopes. Antennas in an [0,1,4,6] Golomb ruler configuration can often be seen at cell sites.

Currently, the complexity of finding optimal Golomb rulers of arbitrary length n is unknown, but it is believed to be an NP-hard problem.[6]

Known optimal Golomb rulers

The following table contains all known optimal Golomb rulers (excluding rulers which are equivalent to one of these with marks in reverse order). The table is complete up to and including order 24.

order length marks
1 0 0
2 1 0 1
3 3 0 1 3
4 6 0 1 4 6
5 11 0 1 4 9 11
0 2 7 8 11
6 17 0 1 4 10 12 17
0 1 4 10 15 17
0 1 8 11 13 17
0 1 8 12 14 17
7 25 0 1 4 10 18 23 25
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 7 13 21 22 25
8 34 0 1 4 9 15 22 32 34
9 44 0 1 5 12 25 27 35 41 44
10 55 0 1 6 10 23 26 34 41 53 55
11 72 0 1 4 13 28 33 47 54 64 70 72
0 1 9 19 24 31 52 56 58 69 72
12 85 0 2 6 24 29 40 43 55 68 75 76 85
13 106 0 2 5 25 37 43 59 70 85 89 98 99 106
14 127 0 4 6 20 35 52 59 77 78 86 89 99 122 127
15 151 0 4 20 30 57 59 62 76 100 111 123 136 144 145 151
16 177 0 1 4 11 26 32 56 68 76 115 117 134 150 163 168 177
17 199 0 5 7 17 52 56 67 80 81 100 122 138 159 165 168 191 199
18 216 0 2 10 22 53 56 82 83 89 98 130 148 153 167 188 192 205 216
19 246 0 1 6 25 32 72 100 108 120 130 153 169 187 190 204 231 233 242 246
20 283 0 1 8 11 68 77 94 116 121 156 158 179 194 208 212 228 240 253 259 283
21 333 0 2 24 56 77 82 83 95 129 144 179 186 195 255 265 285 293 296 310 329 333
22 356 0 1 9 14 43 70 106 122 124 128 159 179 204 223 253 263 270 291 330 341 353 356
23 372 0 3 7 17 61 66 91 99 114 159 171 199 200 226 235 246 277 316 329 348 350 366 372
24 425 0 9 33 37 38 97 122 129 140 142 152 191 205 208 252 278 286 326 332 353 368 384 403 425

As of 2008, the search for optimal Golomb rulers of order 25 is currently underway[5] by distributed.net and is predicted to confirm the following ruler, which was discovered in 1984 by M. D. Atkinson and A. Hassenklover:

order length marks
25 480 0 12 29 39 72 91 146 157 160 161 166 191 207 214 258 290 316 354 372 394 396 431 459 467 480

See also

Notes

  1. ^ S. Sidon, "Ein Satz über trigonometrische Polynome und seine Anwendungen in der Theorie der Fourier-Reihen", Mathematische Annalen 106 (1932), pp. 536–539
  2. ^ Wallace C. Babcock, "Intermodulation Interference in Radio Systems/Frequency of Occurrence and Control by Channel Selection", Bell System Technical Journal 31 (1953), pp. 63–73.
  3. ^ "stats.distributed.net - OGR-24 Overall Project Stats". Retrieved 2008-03-27.
  4. ^ "distributed.net - .plan archives". Retrieved 2008-03-27.
  5. ^ a b "stats.distributed.net - OGR-25 Overall Project Stats". Retrieved 2008-09-22.
  6. ^ Modular and Regular Golomb Rulers

References

Retrieved from "https://en.wikipedia.org/w/index.php?title=Golomb_ruler&oldid=240361309"